|
|
I-THINF WS 0203 - Vorlesung mit Übung |
1. Warum theoretische Informatik?
Im Kreis der vielfältigen Fächer, die im Rahmen eines FH-Studienganges Informatik angeboten werden, muss man dem Fach 'theoretische Informatik' eine ganz besondere Rolle zuweisen: in ihm werden nicht nur die theoretischen Grundlagen des modernen Computers behandelt, sondern noch allgemeiner, die grundlegenden Eigenschaften von berechenbaren Prozessen schlechthin. So geht es um die Frage, was sich überhaupt mit einem Computer berechnen lässt. Eine letztlich sehr praktische Frage, da Sie einen im günstigen Fall in die Lage versetzen kann, die unnötige Verwendung von Betriebsmitteln zu verhindern. Aber selbst für solche Probleme, für die man weiss, dass es zumindest prinzipielle Lösungen gibt, genügt dieses allgemeine Wissen oft nicht; vielmehr muss man wissen, in welcher Zeit und/ oder mit welchem Speicheraufwand ein Problem lösbar ist. Theoretische Möglichkeiten können aus praktischer Sicht u.U. undurchführbar sein. Schliesslich existieren für ein und dasselbe Problem immer mehrere unterschiedliche Herangehensweisen, jede mit ihren typischen Vor- und Nachteilen; auch hier kann die theoretische Informatik helfen, die geeignetste Herangehensweise auszuwählen und zu optimieren.
(Für formale Begriffe, die in dieser Vorlesung benutzt werden, siehe auch die Zusammenstellung wichtiger formaler Begriffe).
2. Der begriffliche Raum der theoretischen Informatik
Es gibt viele Möglichkeiten, sich dem Gegenstand der theoretischen Informatik zu nähern. Im folgenden wird ein Netzwerk von Begriffen vorgestellt, die den begrifflichen Raum der theoretischen Informatik in ihren wesentlichen Aspekten repräsentieren. Es wird Aufgabe der gesamten Lehrveranstaltung sein, diesen begrifflichen Raum mehr und mehr zu präzisieren und mit Beispielen anzureichern.
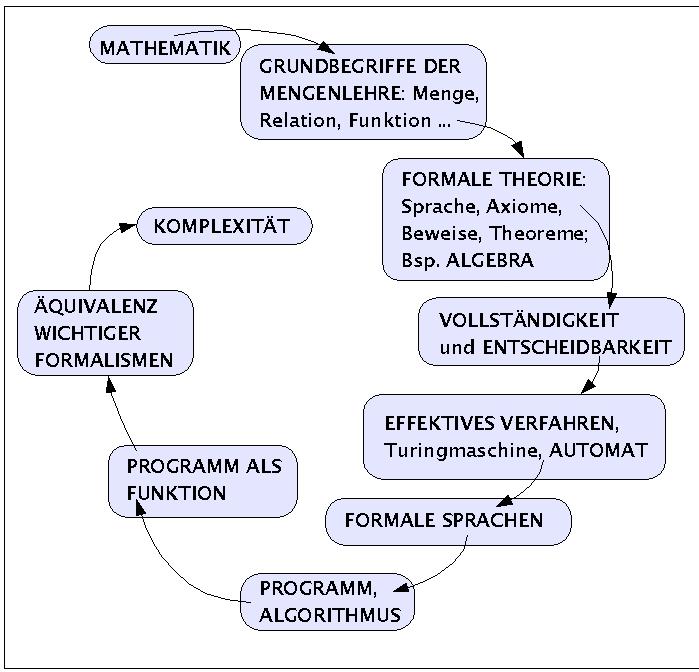
Der begriffliche Raum der Theoretischen Informatik
Zu Beginn des dritten Semesters liegen sowohl Grundkenntnisse der Mathematik vor (insbesondere auch Algebra), wie auch Grundkenntnisse über Computerprogramme und Computer. Beide Begriffsbegreiche, Mathematik und Computer, sind zentral für die theoretische Informatik.
Die moderne Mathematik ist hochgradig formalisiert. Sie bentutzt klar definierte formale Sprachen, um darin Strukturen zu formulieren, deren Eigenschaften auf unterschiedliche Weise nach klaren Schlussregeln bewiesen werden. Die wohl bekannteste und wichtigste formale Sprache, die in der Mathematik benutzt wird, das ist die Sprache der Mengenlehre. Mit ihr lassen sich Begriffe wie 'Menge', 'Elementschaft', 'Teilmenge' usf. definieren, oder dann auch so fundamentale Begriffe wie 'Relation' und 'Funktion'. Die Logik, die zusammen mit der formalen Sprache benutzt wird, ist normalerweise die Prädikatenlogik der ersten Stufe; dies ist eine von vielen hundert Logiksystemen, die in den letzten 100 Jahren eingeführt und untersucht worden sind.
Mit Hilfe der mengentheoretischen Sprache und einer Logik lassen sich dann formale Theorien bilden: eine formale Theorie wird heute in der Regel als ein Tupel definiert, das festlegt, welche Mengen in der Theorie vorkommen sollen, welche Relationen und Funktionen, sowie welche Axiome gelten sollen. Eine Algebra ist ein Beispiel für eine sehr einfache Theorie.
Historisch gesehen waren es gerade Grundlagenprobleme der Mathematik, die letztlich zum Konzept des modernen Computers und der theortischen Informatik geführt haben.
3. Historische Wurzeln der theoretischen Informatik
Stark vereinfachend könnte man es vielleicht so ausdrücken (vgl. zum Folgenden u.a. [KNEALE & KNEALE 1984]): nachdem es BOOLE und FREGE am Ende des 19.Jh. gelungen war, die Logik des Aristoteles (und der Stoa (Chrysipp)) neu zu formalisieren, dabei zu präzisieren und zu erweitern, regte sich begründete Hoffnung, dass man mit dieser rundum erneuerten -nun 'formalen'- Logik möglicherweise die gesamte Mathematik formal rekonstruieren könnte. Diese Anliegen wurde seit FREGE mit dem Schlagwort des Logizismus belegt.
Obwohl die Entdeckung einer Antinomie in FREGES 'Grundlagen der Arithmetik' durch RUSSELL eine erste Krise auslöste, wurde die Hoffnung auf eine Realisierbarkeit des Programms des Logizismus durch das monumentale Werk 'Principia Mathematica'(1910-1913) von WHITEHEAD und RUSSELL (RUSSELL war ein Schüler WHITEHEADS) weiter gestärkt. Darin hatten WHITEHEAD und RUSSELL mit dem Ansatz der Typentheorie das Problem der Antinomie von FREGE gelöst und hatten erste Gebiete der Mathematik mit den Methoden der neuen formalen Logik dargestellt.
Es war HILBERT mit seinem Team, der neben dem Logizismus für eine 'Verschärfung' der Diskussion um die Grundlagen der Mathematik sorgte. Er glaubte zwar nicht, dass man die Mathematik aufgrund der unendlichen Grössen, mit denen sie arbeitet, einfach in die Logik integrieren könnte, aber er benutze die Möglichkeiten der 'neuen' Logik, um eine volle Formalisierung der Mathematik (mit endlich vielen Axiomen) zu fordern, dazu die zusätzliche Forderung nach einer 'Beweistheorie mit finiten Mitteln'; wenigstens die Widerspruchsfreiheit sollte 'konstruktiv' bewiesen werden können (die drei wichtigsten Eigenschaften der Axiome einer formalisierten Theorie sind Widerspruchsfreiheit, Vollständigkeit und Unabhängigkeit). Um die Widerspruchsfreiheit eines Systems S sicherzustellen, muss minimal gelten, dass es wenigstens eine Formel gibt, die nicht ableitbar ist. Dies ist eine andere Formulierung dafür, dass eine Aussage der Form 'P & ~P' nicht ableitbar sein darf, da aus solch einer Formel jede Formel ableitbar wäre.
Es war dann GÖDEL, der in einer genialen Konstruktion zeigen konnte, dass das System der Principia Mathematica, das stark genug war, die Grundlagen der Arithmetik zu formulieren, wesentlich unvollständig ist; 'wesentlich' deshalb, weil jeder Versuch, wahre, aber unbeweisbare, Aussagen dem System hinzuzufügen, notwendigerweise sowohl dazu zwingt, den Beweisbegriff zu erweitern wie auch notwendigerweise neue wahre Aussagen erzeugt, die auch in dem erweiterten System nicht beweisbar sind. Mit diesem prinzipiellen Resultat war klar, dass das Hilbert-Programm als gescheitert betrachtet werden musste: es kann kein formales (mathematisches) System geben, das mindestens so stark ist wie das System der Principia Mathematica (oder äquivalenten wie z.B. das axiomatische mengentheoretische System von Zermelo), dessen Axiome vollständig sind und das zugleich widerspruchsfrei ist. In gewisser Weise kann man auch sagen, dass damit das Programm des Logizismus gescheitert ist: die normale Quantorenlogik ist 'vollständig', nicht aber eine Erweiterung, mit der sich die Arithmetik behandeln lässt, d.h. die 'Logik' endet da, wo die 'Mathematik' anfängt (wobei man sich dann fragen muss, was das denn noch ist, was man da 'Mathematik' nennt, ein notgedrungen 'unvollständiges' und 'widerspruchsvolles' Gebilde...)
Eine kleine Schwachstelle gab es noch in GÖDELs genialem Beweis der Unvollständigkeit. Obwohl er das System der Principia Mathematica vollständig arithmetisierte (eineindeutige Abbildung aller Zeichen und Formeln des Systems in Zahlen) und obwohl er als formales Hilfsmittel weitgehend rekursive Funktionen benutzte, war seine Beweisführung nicht vollständig finit. Dieses Desiderat wurde aber bald durch Church und TURING beseitigt.
Nachdem CHURCH 1936 die Vermutung aufgestellt hatte, dass der Begriff der 'effektiven Berechenbarkeit' ersetzbar ist durch die Begriffe 'rekursiv' (cf. [CHURCH 1936a:95, 100ff]), für den er zeigte, dass er äquivalent ist mit dem Begriff Lamda-Definierbar (cf. [CHURCH 1936a:99]), führt er einen indirekten Beweis, dass der Nachweis der Eigenschaft dass eine beliebige Formel eine Normalform hat, nicht rekursiv ist (cf. [CHURCH 1936a:104f]). Auf dieser Basis kommt CHURCH dann zu dem Ergebnis, dass der Nachweis der Wahrheit oder Falschheit einer beliebigen Formel nicht rekursiv ist (cf. [CHURCH 1936a:107]). Kurze Zeit später (cf. [CHURCH 1936b]) legt CHURCH dann einen 'konstruktiven' Beweis dafür vor, dass das allgemeine Entscheidungsproblem für die Quantorenlogik (erweitert um finite Axiomen für natürliche Zahlen) nicht entscheidbar ist.
Wenngleich später publiziert kam TURING unabhängig von CHURCH zum gleichen Resultat. Für seinen Beweis benutzte er das formalisierte Konzept eines Agenten, der Zeichen auf ein Blatt schreibt, sie wieder löschen kann, und mittels einfacher Operationen sein Ergebnis schrittweise konstruiert. Durch Verwendung dieses Konzeptes -von CHURCH 'Turingmaschine' genannt- führt TURING ebenfalls einen konstruktiven Beweis, dass es unmöglich ist, mittels eines effektiven Verfahrens für eine beliebige Formel der Quantorenlogik zu entscheiden, ob sie beweisbar ist oder nicht. Ferner zeigt er die Äquivalenz von Turingberechenbarkeit und Lamda-Definierbarkeit.
Es ist interessant, dass sowohl GÖDEL wie auch CHURCH selbst meinen, dass das Konzept der Turingmaschine von allen bekannten konstruktiven Verfahren das 'überzeugendste' Verfahren sei.
|
PERSONEN |
SACHVERHALT |
MARKE |
|---|---|---|
|
Georg BOOLE (1815 - 1864) |
Mit seinen Büchern "Mathematical Analysis of Logic" (1847) sowie "Language of Thought" (1854) knüpft Boole an die Tradition der Logik von Aristoteles (384 - 322 v.Chr) und Chrysippos (281/72 - 208/04 v.Chr.) an und behandelt das Thema formal und axiomatisch. Unter anderem gelingt ihm eine Formalisierung der Algebra der Logik, wie sie heute noch in Gebrauch ist. |
Boolsche Algebra |
|
Friedrich L.G. FREGE (1848 - 1925) |
Vor allem mit seiner Schrift "Begriffsschrift" (1879) und der Schrift "Die Grundlagen der Arithmetik" (1884) gelingt es Frege, den Formalisierungsansatz von Boole weiter voranzutreiben; er verfolgt den -später als 'Logizismus' bezeichneten- Ansatz, die gesamte Mathematik als Teil der Logik zu rekonstruieren. |
Logizismus |
|
Albert N. WHITEHEAD (1861 - 1947) |
Nach der Entdeckung der Zermelo-Fraenkelschen Antinomie in Freges Grundlagen der Arithmetik und deren Vermeidung durch Erfindung der Typentheorie unternehmen es beide Autoren, in dem grossen Werk "Principia Mathematica" (Bd.1+2 1910, Bd.3 1913, Neuauflage 1927) das Programm des Logizismus weiter voranzutreiben. |
Logizismus |
|
David Hilbert (1862 - 1943) |
Hilbert glaubte nicht, wie der Logizismus, dass man die Mathematik in die Logik integrieren könnte (u.a. weil die Mathematik mit unendlichen Grössen arbeitet), aber neben der Forderung einer vollständigen Formalisierung und Axiomatisierung der Mathematik stellte er die zusätzlichen Forderungen auf (1917), dass sich in einer voll formalisierten (und axiomatisierten) Mathematik die Widerspruchsfreiheit 'rein syntaktisch' zeigen lassen muss, und zwar mit 'rein finiten Mitteln'. Aus heutiger Sicht könnte man diese Forderung so umformulieren, dass Hilbert gefordert habe, man müsse die Mathematik so formaliseren, dass man mittels eines Computer jede beliebige mathematische Theorie entscheiden kann. |
Hilbert Programm; Beweistheorie |
|
Kurt Gödel (1906 - 1978) |
Nachdem Gödel 1930 zunächst die Vollständigkeit der Quantorenlogik 1.Stufe (in der Version von Frege und Rusell) beweisen konnte, bewies er 1931 die Unvollständigkeit der elementaren Zahlentheorie, genauer: entweder ist die elementare Zahlentheorie vollständig, dann ist sie aber nicht entscheidbar, oder sie ist entscheidbar, dann ist sie aber nicht vollständig. Dieses Ergebnis bedeutete das Aus für Hilberts Programm; schon die elementare Zahlentheorie ist nicht entscheidbar, ganz zu schweigen von all den viel mächtigeren mathematischen Theorien. Allerdings ist Gödels Beweis nach Martin Davis 'nicht vollständig konstruktiv', d.h. er umfasst nicht nur 'finite Mittel'. |
Unvollständigkeit der elementaren Zahlentheorie; Unmöglichkeit des Hilbertprogramms |
|
Alonzo CHURCH (1903 - 1995) |
In einem berühmten Aufsatz "An unsolvable problem of elementary number theory" (1935) stellt Church die Hypothese auf, dass der Begriff 'effektiv berechenbar' ('effectively calculable') identisch ist mit den Begriffen 'Lambda-Definierbarkeit' oder 'allgemein rekursiv' (letzterer Begriff in dem Sinne, wie ihn Herbrand und Gödel definiert haben). Dies ist die Entstehung der berühmten 'Churchschen These'. Er beweist in diesem Aufsatz auch die Unentscheidbarkeit der Principia Mathematica, allerdings unter der Voraussetzung der Gültigkeit des Gödelschen Unvollständigkeitsbeweises, der als solcher nicht 'konstruktiv' ist.In einer späteren Bemerkung "A note on the Entscheidungsproblem" (1936) zeigt Church aber dann doch konstruktiv, dass der engere Funktionenkalkül von Hilbert und Ackermann (1928) unentscheidbar ist. |
Churchsche These; Unentscheidbarkeit der Quantorenlogik; Unmöglichkeit des Hilbertprogramms |
|
Alan M.Turing (1912 - 1954) |
In seinem Aufsatz "On computable numbers, with an application to the Entscheidungsproblem" (1936-7; Korrekturen 1937) führt Turing das später unter dem Namen 'Turingmaschine' bekanntgewordene Konzept eines 'berechenbaren' ('computable') Verfahrens ein, das ausschliesslich finite Mittel benutzt. Er zeigt, dass sein Konzept von 'berechenbar' mit dem Konzept 'effektiv berechenbar' ('effectively calculable') von Church äquivalent ist. Dann beweist er mit Bezug auf den beschränkten Funktionenkalkül von Hilbert/ Ackermann (1931) konstruktiv -unabhängig von Church- , dass der engere Funktionenkalkül von Hilbert und Ackermann (1928) unentscheidbar ist. Die Sonderstellung, die Turings Beitrag einnimmt, wird deutlich, wenn man zwei der Hauptakteure in der Etablierung der Unentscheidbarkeitsresultate zu Wort kommen lässt, nämlich Gödel und Church, hier zitiert aus meinem Artikel über Turing und seine Beziehung zur Semiotik) "While Gödel was not convinced by Church's proof of 1936, he immediately accepted Turing's paper, and in his remark at Princeton in 1946 he stated that 'with this concept [i.e. Turing's computability], one has for the first time succeeded in giving an absolute definition of an interesting epistemological notion, i.e., one not dependent upon the formalism chosen' (cited in Davis 1965:83). And even Church was willing to accept Turing's conceptual approach as convincing when, in his review of Turing, he stated: "Of these methods [Turing's computability, general recursiveness, and lambda-definability], the first has the advantage of making evident immediately the identification effective in the ordinary (not explicitly defined) sense - i.e. without the necessity of proving preliminary theorems. The second and third have the advantage of being suitable for being incorporated within a system of symbolic logic.' (cf. Church 1937). |
Turingmaschine; Unentscheidbarkeit der Quantorenlogik; Turingberechenbar äquivalent zu Lambda-Definierbar (Erweiterung der Churchschen These); Unmöglichkeit des Hilbertprogramms |
4. Funktionen, Sprachen, Automaten und Grammatiken
Der historische Rückblick macht also deutlich, dass und wie die Grundlagendiskussionen in der Logik, in der Mathematik und Metamathematik in der Zeit vom ausgehenden 18.Jh bis etwa Ende des ersten Drittels des 20.Jahrhunderts die Notwendigkeit einer klaren Fassung des Begriffs eines 'effektiven Verfahrens' klar hervortreten liesen. Zugleich wurden erste solche 'Präzisierungen' des Begriffs eines effektiven Verfahren vorgestellt.
Machen wir uns dies nochmals ganz klar (siehe auch Schaubild):
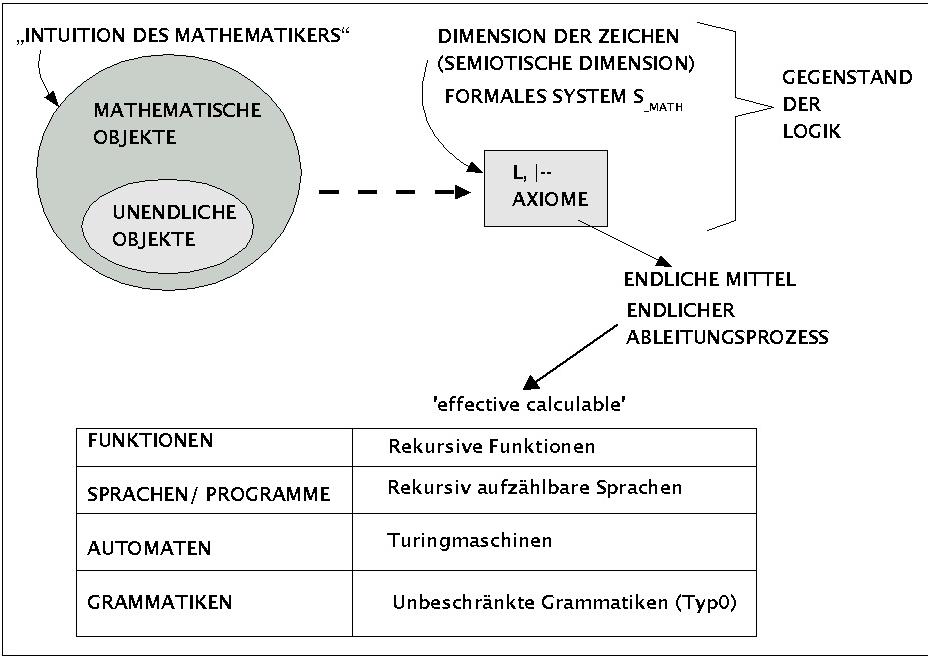
Den Ausgangspunkt bildet die Mathematik des 18.Jh, die mehr und mehr die mathematischen Objekte, die letztlich nur in der Intuition des Mathematikers gegeben sind (wo sonst?), in formalen Systemen (Zeichensystemen) darzustellen versucht.
Parallel hat die moderne Logik versucht, den Begriff der 'wahrheitserhaltenden' Folgerung zu formalisieren. Eine logische Theorie ist eine solche, in der mit einer Sprache L' beschrieben wird, welche Objekte einer Sprache L auf welche Weise mithilfe von logischen Schlussregeln in andere Objekte der Sprache L umgeformt (bzw. gefolgert) werden können. Die Menge der Schlussregeln bildet den Folgerungsbegriff und wird oft durch das Zeichen '|--' dargestellt. Die Sprache L der Objekte heisst auch Objektsprache und die Sprache L' über die Objekte der Objektsprache samt den Schlussregeln heisst die Metasprache.
Der Gewinn an Klarheit, den die Einführung formaler Systeme in der Mathematik mit sich brachte, war bei der beständig ansteigenden Komplexität der mathematischen Theorien auf Dauer aber nur zu halten, wenn es möglich war, die grundlegenden Eigenschaften eines formalen Systems (Widerspruchsfreiheit, Vollständigkeit, Unabhängigkeit) jederzeit zweifelsfrei nachweisen zu können; andernfalls wäre die 'Klarheit der Formelsprache' nur eine 'scheinbare' Klarheit; ein formales System z.B., dessen Widerspruchsfreiheit man nicht mehr nachweisen könnte, ist letztlich unbrauchbar, da man dann alles beweisen könnte, was man will.
Die Forderung, dass wenigstens die Widerspruchsfreiheit einer mathematischen Theorie zweifelsfrei nachweisbar sein sollte (Hilbert-Programm), führte dann zu der Frage, wann denn ein Beweis wohl 'zweifelsfrei' wäre. Es bildete sich die Überzeugung, dass ein effektiv berechenbares ('effectiv calculable') Verfahren nur ein solches sein könnte, das mit endlichen ('finite') Mitteln arbeitet. Konkret heisst dies z.B., dass die Anzahl der Axiome eines formalen Systems endlich sein muss. Aber auch der Ableitungsprozess selbst, der Übergang von den aktuell als 'wahr' geltenden Ausdrücken des Systems zu einem 'neuen', 'wahrheitserhaltenden' Ausdruck, muss mit 'endlichen Mitteln' geschehen. Ferner sollte die Anzahl aller Schritte bis zu dem zu beweisenden Ausdruck endlich sein.
Das erste begriffliche Hilfsmittel, mit dem man glaubte, ein entsprechendes 'effektives Verfahren' gefunden zu haben, waren die rekursiven Funktionen (in diesem Sinne erstmalig genutzt von HERBRAND und GÖDEL). Dieser Typ von Funktionen ist in der Tat von einer bestechenden Einfachheit und wird bis heute in vielen Theoriebildungen benutzt.
Die Eingabe- und Ausgabewerte von rekursiven Funktionen kann man ganz allgemein als Zeichenketten auffassen. Zeichenketten, die bestimmten Anforderungen genügen, um korrekte Ausdrücke zu sein, bilden aber auch eine Sprache; jedes (Computer-)Programm ist in diesem Sinne auch ein korrekter Ausdruck einer bestimmten Sprache.
Nahezu parallel zur Klassifizierung von rekursiven Funktionen als ein Mittel zur Realisierung von effektiven Verfahren wurde auch das Verfahren von TURING, seine Turingmaschine, als solch ein effektives Verfahren klassifiziert. Seine Äquivalenz mit den rekursiven Funktionen wurde bewiesen. Turingmaschinen können rekursive Funktionen gleichsam 'simulieren': angenommen eine rekursive Funktion f mit Argument x liefert das Ergebnis y (f(x) = y), dann kann man eine Turingmaschine definieren, die angesetzt auf ein Argument x den Wert y berechnet. Entsprechend kann man auch zwischen Turingmaschinen und Sprachen eine Beziehung herstellen. So heissen z.B. die Sprachen, die von einer Turingmaschine erkannt werden können, die rekursiv aufzählbaren Sprachen.
Weiterhin entdeckte man, dass sich 'effektive Verfahren' auch in der Form von Ersetzungssystemen realisieren lasssen. Ersetzungssysteme sind darstellbar als eine Struktur mit einer Menge von Ausdrücken einer Sprache L, über denen eine endliche Menge von Ersetzungsregeln P definiert ist. Damit lassen sich dann aus gegeben Ausdrücken andere Ausdrücke erzeugen. Diese Struktur erinnert an die Ableitungssysteme der Logik. Man kann sie aber auch als formale Grammatiken auffassen. Letztlich definiert eine solche Grammatik eine Menge erzeugbarer Ausdrücke, die eine Sprache bilden. Es konnte gezeigt werden, dass diejenigen Sprachen, die von einer Turingmaschine erkannt werden können (:= rekursiv aufzählbare Spachen) identisch sind mit den Sprachen, die eine sogenannte unbeschränkte Grammatik erzeugen kann. In der später einzuführenden Chomsky-Hierarchie sind dies die Typ0-Grammatiken bzw. Typ0-Sprachen.
In der Praxis zeigte sich, dass rekusive Funktionen, Turingmaschinen, rekursiv aufzählbare Sprachen bzw. unbeschränkte Grammatiken noch viel zu mächtig sind. In den meisten Anwendungsfällen genügen weit schwächere Strukturen. Es wurden von daher mehr und mehr auch abgeschächte Versionen effektiver Verfahren untersucht.
5. Eine Hierarchie von Automaten, Sprachen und Grammatiken
Wie eben schon angedeutet, ist eine Turingmaschine (oder eines der ihr äquivalenten Verfahren) in der Praxis oft viel zu mächtig. Schwächere Verfahren genügen in vielen Fällen und sie sind dann auch in der Regel schneller und benötigen weniger Platz. Die nachfolgende Tabelle gibt einen ersten Überblick über die heute bekannte Hierarchie von Automaten und Sprachen bzw. Grammatiken (weitere Verfeinerungen werden später erläutert).
|
AUTOMATEN |
SPRACHEN/ MENGEN |
GRAMMATIKEN |
|---|---|---|
|
Überabzählbare Mengen |
||
|
Abzählbare Mengen |
||
|
Turingmaschine (TM) |
rekursiv aufzählbare Sprachen = turing-erkennbare Sprachen = Typ0-Sprachen |
Unbeschränkte Grammatiken = Typ0-Grammatiken = Phrasenstruktur-Grammatiken |
|
Stehts haltende Turingmaschine (TM) |
turing-entscheidbare Sprachen |
|
|
Linear beschränkter Automat (LBA) |
kontextsensitive Sprachen (CSL) = Typ1-Sprachen |
Kontextsensitive Grammatiken (CSG) = Typ1-Grammatiken |
|
Kellerautomat ('pushdown automaton') (PDA) |
Kontextfreie Sprachen (CFL) = Typ2-Sprachen |
Kontextfreie Grammatiken (CFG) = Typ2-Grammatiken |
|
Deterministischer Kellerautomat ('deterministic pushdown automaton') (DPDA) |
Deterministische kontextfreie Sprachen (DCFL) = LR(k)-Sprachen |
Deterministische kontextfreie Grammatiken (DCFG) = LR(k)-Grammatiken |
|
Deterministischer endlicher Automat ('deterministic finite automaton') (DFA)/ Nichtdeterministischer endlicher Automat ('nondeterministic finite automaton') (NFA) |
Reguläre Sprachen = Typ3-Sprachen |
Reguläre Grammatiken = Typ3-Grammatiken = Reguläre Ausdrücke |
|
Endliche Mengen |
Aufzählung |
Ziel der Lehrveranstaltung ist es, ein grundlegendes Verständnis aller dieser verschiedenen Formen von effektiven Verfahren zu gewinnen, ihr Verhältnis untereinander sowie ihre Anwendbarkeit in der Praxis zu klären.
In der Komplexitätstheorie wird die 'Komplexität' ('complexity') eines Problems gemessen am Ressourcenbedarf für seine Repräsentation und für seine Lösung. Neben der Ressource 'Platz' ('space') ist es vor allem der 'Zeitbedarf' ('time'), der zur Charakterisierung benutzt wird.
Bilden sie ein Team von 5 Mitgliedern
Erstellung Sie gemeinsam einen Texte (min. 1 Seite, max. 3 Seiten) mit Namen und Matr.Nr. der AutorenInnen. Abgabe einer Kopie des Textes an den Dozenten vor Beginn der Vorlesung.
Präsentation der Lösung als Team vor der gesamten Gruppe. Präsentationszeit (abhängig von der Gesamtzahl der Teams) 3-5 Min.
Versuchen Sie in dem Text Antworten auf folgende Fragen zu formulieren:
Was ist eine formale Theorie?
Wie würden Sie die Begriffe 'Widerspruchsfreiheit', 'Vollständigkeit' und 'Unabhängigkeit' für formale Theorien erklären?
Geben Sie irgendein Beispiel einer möglichst einfachen formalen Theorie
Wie könnte man ein Theorem für diese Theorie beweisen?
Was bedeutet es, wenn man verlangt, dass ein Beweis mit 'finiten Mitteln' geführt werden soll?