1. Basisbegriffe aus der Mengenlehre




2. Rekursive Funktionen und Prädikate




3. Graphen




4. Bäume




5. Strukturtheorie




6. Algebra




7. Masstheorie




8. Wahrscheinlichkeitstheorie




9. Bayessche Netze




10. Optimierungstheorie




11. Maschinelles Lernen




12. Formale Sprachen




13. Automaten




14. Komplexitätstheorie

GRUNDLAGEN DER INFORMATIK/ THORETISCHE INFORMATIK - Mengentheoretische Notation

Basisbegriffe aus der Mengenlehre

1. Der Begriff Menge ist ein Grundbegriff. Alle Elemente in einer Menge kommen nur einmal vor.

   
   

2. Endliche Mengen kann man angeben durch Aufzählen der Elemente, z.B. {1,2,3,4,a,b,c}.

   
   

3. Unendliche Mengen kann man angeben über die sie definierenden Eigenschaften, z.B. {x| P(x)}, die Menge der x, für die gilt, dass die Eigenschaft P auf sie zutrifft.

   
   

4. ∈ := x ist Element von y

   
   

5. ∉ := x ist nicht Element von y ¬(x ∈ y)

   
   

6. (a,b) := Das geordnete Paar von a und b; (a,b) = {{a}, {a,b}} /* Definition nach Wiener (1914) und Kuratowski (1921) */

7. Satz: (x,y) = (u,v) ==> x = u & y = v

8. Satz: x != y ==> (x,y) != (y,x)
   

9. pr1(p) := die erste Projektion von p; pr1(p) = u gdw p ist ein geordnetes Paar & (E:v)( p = (u,v) )

   
   

10. pr2(p) := die zweite Projektion von p; pr1(p) = u gdw p ist ein geordnetes Paar & (E:v)( p = (v,u) )

    
    

11. C := Teilmenge; x C y = {a| ∈ x dann a ∈ y}

    
    

12. u := Vereinigung von x und y; x u y = {a| a ∈ x oder a ∈ y }

    
    

13. U := Grosse Vereinigung von X: U (X) = {z | (E:y)(y ∈ X & z ∈ y ) }

    
    

14. cut := Durchschnitt; x cut y = {a| a ∈ x und a ∈ y }

    
    

15. CUT := Grosser Durchschnitt von X: CUT (X) = {z | (A:y)(y ∈ X ==> z ∈ y ) }

    
    

16. - := Differenz; x - y = {a| a ∈ x und a ∉ y }

    
    

17. x := Operator zur Erzeugung von Paarmengen; seien X und Y Mengen: X x Y

    
    

18. Eine Relation (REL) ist eine Menge von geordneten Paaren; sei REL(R), dann gilt, es gibt Mengen X und Y mit R C X x Y. Ist X = Y, dann ist eine Relation R eine Relation auf ('on') X. Gilt (a,b) ∈ R, kann man auch schreiben aRb. Folgende Eigenschaften sind bei Relationen von Interesse:

    
    

    1. rn:= range/ Wertebereich einer Relation R; rn(R) = {y | (E:x)( xRy ) }

       
       

    2. dm := domain/ Definitionsbereich einer Relation R; dm(R) = {x | (E:y)( xRy ) }

       
       

    3. fd := field/ Feld einer Relation R; fd(R) = dm(R) u rn(R)

       
       

    4. R^-1 := die Konverse einer Relation R; (y,x) ∈ R^-1 gdw (x,y) ∈ R

       
       

    5. R^{``</sup>A := das R-Bild von A; R<sup>``}A = { y | (E:x)( x ∈ A & (x,y) ∈ R ) }

    6. R^''A := das R-UrBild von A; R^''A = { x | (E:y)( y ∈ A & (x,y) ∈ R )

    7. R /| A := die Linksbeschränkung von R auf A; R /| A = { p | p ∈ R & pr1(p) ∈ A }

    8. R |\ A := die Rechtsbeschränkung von R auf A; R |\ A = { p | p ∈ R & pr2(p) ∈ A }

    9. R /|\ A := die Totalbeschränkung von R auf A; R /|\ A = { p | p ∈ R & p ∈ A x A } }

       
       

    10. Reflexivität: aRa für alle a

        
        

    11. Irreflexivität: Für alle a gilt ¬(aRa)

        
        

    12. Transitivität: aRb und bRc impliziert aRc

        
        

    13. Symmetrie: aRb impliziert bRa

        
        

    14. Assymetrie: aRb impliziert bRa

        
        

    15. Rechtseindeutig: aRb & aRc impliziert b = c

        
        

    16. Linkseindeutig: aRb & cRb impliziert a = c

        
        

    17. SURJEKTIV(R) gdw (E:a,b)( R C a x b & RECHTSEINDEUTIG(R) & b C rn(R) )

        
        

    18. Äquivalenzrelation: R ist symmetrisch und transitiv. Es gilt z.B. dm(R) = rn(R) und R ist reflexiv. Äquivalenzrelationen zerlegen das Feld einer Relation vollständig und disjunkt in Teilklassen, d.h. der Durchschnitt von zweien solchen Teilklassen ist leer. Diese durch eine Äquivalenzrelation R induzierte Teilklassen heissen Äquivalenzklassen bzgl. R.

        
        

    19. [A]_R := A ist eine Äquivalenzklasse bzgl. R und man nennt A den Repräsentanten der Äquivalenzklasse; [A]_R gdw R ist eine Äquivalenzrelation & (E:u) u ∈ A & (A:u)( u ∈ A ==> (A:v)( v ∈ A <==> (u,v) ∈ R) ).

        
        

    20. Index(R) := Wenn R Äquivalenzklasse ist, dann die Anzahl der verschiedenen Äquivalenzklassen, die R hat; falls Index(R) < Unendlich, dann hat R einen endlichen Index (s.u.).

        
        

    21. P-Abschluss (oder die P-Hülle) ('P-Closure') einer Relation R: sei P eine Menge von Eigenschaften einer Relation R. Dann ist der P-Abschluss der Relation R die kleinste Relation R' für die gilt, dass sie alle Paare von R enthält, die die Eigenschaft P haben.
        Beispiel 1: Sei R⁺ der transitive Abschluss von R. Er wird vereinbart mit:

        
        

        1. Wenn (a,b) in R dann (a,b) ∈ R⁺

           
           

        2. Wenn (a,b) in R⁺ und (b,c) ∈ R, dann (a,c) in R⁺

           
           

        3. Nichts ist in R⁺ ausser dem, was in (1) und (2) vereinbart wurde.

           
           
        
        

        Beispiel 2: Der reflexive transitive Abschluss von R, geschrieben R*, wird erreicht durch R⁺ u { a | (a,a) ∈ R }

        
        

    22. Hintereinanderausführung von zwei Relationen R,S: R o S = { (a,b) | (E:z)( aRz & zSb )}

        
        

    23. Funktion (FN) : Eine Relation R ist eine Funktion gdw R ist rechtseindeutig.

        f ist eine Abbildung der Menge A in die Menge B gdw FN(f) & A C dm(f); dann schreibt man auch f: A ---> B. Statt (a,b) ∈ f schreibt man auch f(a) = b oder f'a = b.

        
        

    24. Eine Funktion f ist injektiv gdw sie zusätzlich noch linkseindeutig ist. Anders: |f^-1(b)| < 1 für jedes b ∈ rn(f).

        
        

    25. Eine Funktion f ist surjektiv gdw |f^-1(b)| > 1 für jedes b ∈ rn(f).

        
        

    26. Eine Funktion f ist bijektiv gdw |f^-1(b)| = 1 für jedes b ∈ rn(f).

        
        
    
    

19. pow(x) oder 2^x := Potenzmenge von x; Menge aller Teilmengen

    
    

20. M ist Halbordnung unter R: HALBORDNUNG(M,R) gdw ( (A:a,b,c)(a,b,c ∈ M => R C M x M &
    (a,a) ∈ R &
    (a,b) ∈ R & (b,c) ∈ R => (a,c) in R &
    (a,b) ∈ R & (b,a) ∈ R => a=b )
    
    Beispiel für eine Halbordnung wäre die Menge der natürlichen Zahlen Nat (s.u.) mit der Relation '>'.




21. Kette oder lineare Ordnung unter R:
    KETTE(M,R) gdw HALBORDNUNG(M,R) & (A:a,b)(a,b in M => (a,b) ∈ R or (b,a) ∈ R )




22. Obere Schranke in T von M unter R: s=obSch(T,M,R) gdw HALBORDNUNG(M,R) & T C M & (A:t)(t ∈ T => (t,s) ∈ R ) )




23. Untere Schranke in T von M unter R: s=unSchr(T,M,R) gdw HALBORDNUNG(M,R) & T C M & (A:t)(t ∈ T => (s,t) ∈ R ) )




24. Obere Grenze/ Supremum in T von M unter R: o=sup(T,M,R) gdw (E:S)( S = { s | s=obSchr(T,M,R)} & o ∈ S & ¬(E:t)(t ∈S & (t,o) ∈ R) ) )




25. Untere Grenze/ Infimum in T von M unter R: o=inf(T,M,R) gdw (E:S)( S = { s | s=unSchr(T,M,R)} & o ∈ S & ¬(E:t)(t ∈S & (o,t) ∈ R) )) )




26. Bedingt vollständig M unter R: BEDINGT_VOLLSTAENDIG(M,R) gdw
    HALBORDNUNG(M,R) & (A:T)( T C M & ¬(T = 0) & (E:s)( s=obSchr(T,M,R)) => (E:o)(o=sup(T,M,R)))




27. Vollständig M unter R: VOLLSTAENDIG(M,R) gdw
    HALBORDNUNG(M,R) & (A:T)( T C M & (E:s)( s=obSchr(T,M,R)) => (E:o)(o=sup(T,M,R)))




28. T ist Anfang von M unter R: ANFANG(T,M,R) gdw
    KETTE(M,R) & T C M & ¬(T = 0) & (E:s)( s ∈ M & ¬s ∈ T ) &
    (A:t,r)( t ∈ T & r ∈ T u M & (r,t) ∈ R => r ∈ T ))




29. Der durch k bestimmte Abschnitt in M:
    Abschn(k,M) = { t | (E:R)(KETTE(M,R) & t in M & (t,k) ∈ R ) }




30. T ist offener Anfang von M unter R: OFFENER_ANFANG(T,M,R) gdw
    ANFANG(T,M,R) & (A:t)( t ∈ T => ¬(E:r)( (t,r) ∈ R ))




31. suc(x) := Nachfolger von x; suc(x) = x u {x}

    
    

32. Die natürlichen Zahlen (Nat) wurden zuerst von Peano axiomatisch charakterisiert; später gab es weitere Charakterisierung auf der Basis einer axiomatischen Mengenlehre. Wir benutzen hier eine Charakterisierung in Anlehnung an Peano, weil diese dem konstruktivistischen Ansatz einer Theorie der Berechenbarkeit näher ist:

    
    

    1. 0 ∈ Nat

       
       
    
    

    2. (A:x)( x ∈ Nat => suc(x) ∈ Nat )

    
    

    3. (A:x)( x ∈ Nat => ¬(suc(x) = 0 ) )

    
    

    4. (A:x,y)( suc(x) = suc(y) => x = y )

    
    

    5. (A:M)( [ 0 ∈ M & (A:n)( n ∈ M => suc(n) ∈ M)] => M = Nat )

    
    

33. vg := Vorgänger; vg = suc|\ Nat^-1

    
    .

34. Satz: vg(suc(x)) = x

    
    

35. Satz: (A:x)(x ∈ Nat - 0 => suc(vg(x)) = x

    
    

36. Summe s(x,y) [x + y]
    (A:x,y)( x,y ∈ Nat =>
    s(x,1) = suc(x)
    s(x,nf(y)) = suc(s(x,y))




37. Produkt p(x,y) [x * y]
    (A:x,y)( x,y in Nat =>
    p(x,1) = x
    p(x,suc(y)) = p(x,y) + x
    




38. Kleiner x < y
    (A:x,y)( x,y ∈ Nat =>
    x < y gdw (E:z)( z ∈ Nat & x + z = y )




39. Satz: Die Relation '<' is transitiv, antisymmetrisch und antireflexiv




40. Positive/ Negative/ Nullpaare: (A:x,y)( (x,y) ∈ Nat x Nat =>
    POSITIV(x,y) gdw x < y
    NEGATIV(x,y) gdw x > y
    NULLPAAR(x,y) gdw x = y
    




41. Äquivalent [~] (A:x,y,a,b)( (x,y), (a,b) ∈ Nat x Nat =>
    ÄQUIVALENT((x,y),(a,b) gdw y + a = x + b
    (x,y) ~ (a,b) gdw y + a = x + b
    




42. Positive/ Negative Zahl/ Null/ Ganze Zahlen (Int)
    POSITIVE_ZAHL(a,b) = { (a,b) ∈ Nat x Nat | POSITIV(a,b) & [(a,b)]_~}
    NEGATIVE_ZAHL(a,b) = { (a,b) in Nat x Nat | NEGATIV(a,b) & [(a,b)]_~}
    ZAHL_NULL(a,b) = { (a,b) in Nat x Nat | NULLPAAR(a,b) & [(a,b)]_~ } (ZAHL_NULL(a,b) auch geschrieben '0')
    Ganze_Zahlen = { POSITIVE_ZAHL(a,b) u NEGATIVE_ZAHL(a,b) u ZAHL_NULL(a,b) } (Ganze_Zahlen auch geschrieben 'Int')
    
    Verabredung: Statt [(a,b)]_~ soll auch geschrieben werden (a,b)




43. (+c) = (a,b) gdw POSITIVE_ZAHL(a,b) & c = b - a




44. (-c) = (a,b) gdw NEGATIVE_ZAHL(a,b) & c = a - b




45. Summe((a,b), (x,y)) [(a,b) + (x,y)]
    (A:x,y,a,b)( (a,b), (x,y) ∈ Int =>
    (a,b) + (x,y) = (a + x,b + y)




46. Satz: (A:x,y)( (x,y),0 ∈ Int => (x,y) + 0 = (x,y) )




47. Satz: (A:x,y,a,b)( (a,b), (x,y) ∈ Int =>
    (E:mn)((m,n) ∈ Int & ((a,b) + (m,n) = (x,y)) ) )




48. Subtraktion s((a,b), (x,y)) [(a,b) -(x,y)]
    (A:x,y,a,b,m,n)( (a,b), (x,y), (m,n) ∈ Int &
    (a,b) + (m,n) = (x,y)) =>
    (m,n) = (a,b) - (x,y)




49. Produkt p((a,b), (x,y)) [(a,b) * (x,y)]
    (A:x,y,a,b)( (a,b), (x,y) ∈ Int =>
    (a,b) * (x,y) = (a*y + b*x, a*x + b*y)




50. Satz: (A:x,y)( (x,y) ∈ Int => (x,y) * 0 = 0




51. Verabredung c <=> (+c)
    Zwischen den natürlichen Zahlen und den ganzen Zahlen soll folgende Zuordnung gelten:
    (A:c,d,(+c),(+d))( c,d ∈ Nat & (+c), (+d) ∈ Int =>
    [c <=> (+c)] & [d <=> (+d)] => [ c+d <=> (+(c +d))])




52. Satz: (A:(+c),(-c))( (+c), (-c) in Int => (+c) + (-c) = 0
    




53. Satz: (A:(+c),(+d))( (+c), (+d) in Int => (+c) + (+d) = (+(c +d)) )
    




54. Satz: (A:(+c),(+d))( (+c), (+d) in Int => (+c) * (+d) = (+ c * d) )
    




55. Satz: (A:(+c),(-d))( (+c), (-d) in Int => (+c) * (-d) = (- c * d) )
    




56. Satz: (A:(-c),(-d))( (-c), (-d) in Int => (-c) * (-d) = (+ c * d) )
    




57. Äquivalenz für ganze Zahlen [~~] (A:x,y,v,u)(x,y,v,u ∈ Int =>
    (y/x ~~ v/u) gdw ( ¬(x = 0) ) & ¬(u = 0) & u*y = v*x ) )




58. Satz: (A:x,y,v,u)(x,y,v,u ∈ Int =>
    (y/x ~~ v/u) gdw ( v/u ~~ y/x) )
    




59. Satz: (A:x,y)(x,y ∈ Int =>
    (y/x ~~ y/x) )
    




60. Satz: (A:x,y,v,u, m,n)(x,y,v,u,m,n ∈ Int =>
    (y/x ~~ v/u) & ( v/u ~~ m/n) => (y/x ~~ m/n))
    




61. Satz: (A:x,y,z)(x,y,z ∈ Int => y/x ~~ z*y/ z*x )
    




62. Rationale Zahlen (Rat)
    RATIONALE_ZAHL(x,y) = { x,y in Int & [x/y]_~~ }




63. Satz: (A:x,y,v,u)(x,y,v,u ∈ Int & y/x ~~ v/u =>
    [y/x]_~~ = [v/u]_~~ & fraction(y,x) = fraction(v,u) )
    
    Ein Bruch ('fraction') fraction(y,x) ist also eine rationale Zahl, die durch die Klasse der zu y/x äquivalenten Paare gegeben ist.




64. Satz: (A:x,y,z)(x,y,z ∈ Rat =>
    fraction(y,x) = fraction(z*y,z*x) )
    
    




65. Summe s(p,q) [p + q]
    (A:p,q,y,z,u,x)(p,q,x,y,u,z ∈ Rat & p = [y/z]_~~ & q = [u,x]_~~ =>
    p + q = fraction(x*y + z*u, x*z) )




66. Vereinbarung: fraction(y,1) = y




67. Satz: fraction(0,1) = 0




68. Satz: 0 + fraction(x,y) = fraction(x,y)




69. Produkt p(m,n) [m * n]
    (A:m,n,y,z,u,x)(m,n,y,z,u,x ∈ Rat & m = fraction(y/z) & n = fraction(u,x) =>
    m * n = fraction(y*u,z*x) )




70. Satz:
    (A: y, u )(y,u ∈ Rat =>
    fraction(y,1) * fraction(u,1) = fraction(y*u,1) = y * u




71. Satz:
    (A: p,q,u,a,b,y)(p,q,u,a,b,y ∈ Rat & p=fraction(y,a) & q=fraction(u,b) & ¬(p = 0) =>
    (1:r)( r=fraction(q,p) = fraction(u*a,b*y) & p*r = q ))




72. Division q:p
    (A: r,p,q,u,a,b,y)(r,p,q,u,a,b,y ∈ Rat & p=fraction(y,a) & q=fraction(u,b) & ¬(p = 0) & r=fraction(q,p) & p*r = q )) => q:p = r )
    
    R heisst der Quotient von p und q.




73. Satz: (A:k,M)( M = Abschn(k,Rat) & k ∈ Rat => (E:R)( OFFENER_ANFANG(M,Rat,R) ))




74. Menge der rellen Zahlen (Rel):
    Rel = { r | (E:R)( OFFENER_ANFANG(r,Rat,R) ) }




75. r <_Rel s gdw
    r,s ∈ Rel & r C s




76. Satz:KETTE(Rel, <_Rel)




77. Satz: Jeder offene Anfang in Rel ist der Abschnitt einer reellen Zahl




78. Eine Kette M ist dicht unter R: DICHT(M,R) gdw
    KETTE(M,R) & (A:a,b)( a,b ∈ M & (a,b) ∈ R => (E:c)( c ∈ M & (a,c) ∈ R & (c,b) ∈ R ))




79. Satz: Die Menge Rat der rationalen Zahlen ist geordnet, offen und dicht.




80. Satz: Die Menge Rel der reellen Zahlen ist geordnet, offen, dicht und bedingt vollständig.




81. Sei x eine Menge, dann wird durch |x| die Kardinalität der Menge (x die Anzahl der Elemente) repräsentiert.

82. Zwei Mengen x1 und x2 haben die gleiche Kardinalität, wenn es eine 1-zu-1-Abbildung zwischen x1 und x2 gibt.

83. Seien x, y endliche Mengen und sei x C y; dann gilt |x| <= |y|.

84. Wenn x,y keine endliche Mengen sind, dann folgt aus der Teilmengeneigenschaft nicht notwendigerweise eine kleinere Kardinalität!

    
    

85. |Nat| < |Rel|

    
    

86. Mengen mit der gleichen Kardinalität wie die natürlichen Zahlen gelten als abzählbar unendlich ('countably infinite').

87. Eine Menge M heisst (höchstens) abzählbar ('countable') falls sie endlich ist oder abzählbar unendlich. Falls M ungleich 0 kann man auch sagen, es gibt eine surjektive Abbildung f: N' --> M.

    
    

88. epow(x) oder e2^x := Endliche Potenzmenge von ...; Menge aller endlichen Teilmengen

    
    

89. Während die Menge A* zu einem Alphabet A abzählbar unendlich ist, ist die Menge aller Sprachen über A* -nämlich x^(A*) = { L | L C A* } - nicht mehr abzählbar, d.h. überabzählbar.

    
    

90. (M/n) := Die Menge der n-elementigen Teilmengen der Menge M; (M/n) = { x | x C M & |x| = n }

    
    

91. f ist eine Folge [SEQ(f)] gdw f ist eine Funktion & dm(f) C Nat & (A:x)( x in dm(f) & x > 0 ==> x in dm(f) & vg(x) in dm(f))

    
    

92. l ist die Länge einer Folge f [len(f)] SEQ(f) => len(f) = |dm(f)|

    
    

93. f ist eine endliche Folge gdw f ist eine Folge & ¬(Nat' C dm(f)

    
    

94. f ist eine Folge der Länge n gdw f ist eine Folge & ([ n=0 & f=0] or [n ∈ Nat' - {0} & vg(n) ∈ dm(f) & n ∉ dm(f)])

    
    

95. f ist ein n-Tupel ([TUP(f,n)] gdw f ist eine Folge der Länge n. Wir schreiben ein 5-Tupel z.B. t = <a,ww,e,t,g> = {(0,a), (1,ww),(2,e),(3,t),(4,g),}. t(1) = ww.

    
    

96. f ist eine endliche Folge auf A [FSON(f,A)]: FSON(f,A) gdw f ist eine Folge & ¬(Nat' C dm(f)) & rn(f) = A

    
    

97. SUM(i=n1, j) A[i]: Summenbildung über dem Ausdruck A, in dem der Parameter i vorkommt und die Werte von n1 bis j durchläuft.

    
    

Rekursive Funktionen und Prädikate

Im Zusammenhang des Themas Berechenbarkeit/ Entscheidbarkeit wichtige Begriffe: primitiv rekursive Funktionen, Ackermann Funktion, my-rekursive Funktionen, allgemein rekursive Funktionen, rekursive Prädikate

Graphen

1. Ein GRAPH(g) gdw g = <V,E> V ist eine endlichen Menge von Knoten ('vertices', 'nodes'), E ist eine Menge von Paaren von Knoten genannt Kanten ('edges'). E C (V/2) (eine Teilmenge der Menge aller 2-elementigen Teilmengen von V)(Anmerkung: keine Menge von geordneten Paaren, da die Kanten im allgemeinen Fall nicht gerichtet sind!).

   
   

2. Mit GRAPH(g) soll gelten: vertices(g) = proj1(g)

   
   

3. Mit GRAPH(g) soll gelten: edges(g) = proj2(g)

   
   

4. Mit k ∈ edges(g) & k = {x,y} soll gelten: x,y sind in g benachbart ('adjacent'), k verbindet x mit y, x und y sind die Endpunkte von k, x und y sind mit k inzident.

   
   

5. Man kann auch sagen, dass ein Graph g verstanden werden kann als eine Menge V auf der eine Relation R definiert is, die irreflexiv und symmetrisch ist, d.h. für beliebige zwei Knoten x,y aus V muss gelten: xRy.

   
   

6. Vollständiger Graph (simplex) := ein Graph in dem je zwei Knoten benachbart sind.

   
   

7. Gerichteter Graph ('directed graph') := ein Graph für den gilt, dass E C V x V.

   
   

8. Sei g ein gerichteter Graph; mit k ∈ edges(g) & k = (x,y) soll gelten: x ist der Anfangspunkt und y der Endpunkt von k.k führt von x nach y. Grafisch werden gerichtete Kanten als Pfeile dargestellt (im Englischen heisst es hier nicht 'arrow' (!) sondern 'arc'). Eine Kante k = (x,x) heisst eine Schlinge.

   
   

9. Kantenfolge (Pfad, 'path'): Sei g ein Graph; sei f eine Folge der Länge n mit Werten aus der Menge der Knoten V 'e₁, e₂,..., e_n' so dass für zwei aufeinanderfolgende Elemente (e_i, e_i+1) der Folge gilt, es gibt eine Kante k aus E. Ein Pfad enthält keine Schlingen, aber er kann zyklisch sein, wenn der Endknoten e_n mit dem Anfangsknoten e₁ verbunden ist.

   
   

10. Die Länge eines Pfades, der durch eine Folge mit Länge n repräsentiert wird, ist n-1.

    
    

11. Vorgängerknoten, Nachfolgerknoten: Wenn (e_i, e_i+1) zwei verbundene Knoten in einem gerichteten Graphen sind, dann ist e_i der Vorgänger(knoten) von e_i+1 und e_i+1 der Nachfolger von e_i

    
    

Bäume

Ein Baum ('tree') ist ein geordneter Graph mit den folgenden zusätzlichen Eigenschaften:

1. Es gibt genau einen Knoten, der die Wurzel ('root') darstellt.

   
   



2. Die Wurzel hat keinen Vorgängerknoten

   
   



3. Von der Wurzel gibt es einen Pfad zu jedem Knoten im Baum

   
   



4. Jeder Knoten ausser der Wurzel hat genau einen Vorgängerknoten




5. Die Nachfolgerknoten von jedem Knoten sind 'von links nach rechts' geordnet.

Abweichend von der Graphen-Terminologie gibt es bei Bäumen eine spezielle Terminologie:

1. Der Nachfolgerknoten eines Knoten wird Kindknoten ('son', 'child') genannt.




2. Der Vorgängerknoten eines Knoten heisst Elternknoten ('father', 'parent').




3. Gibt es einen Pfad von e_i nach e_j (j > i), dann ist e_i ein Vorfahre ('ancestor') von e_j und e_j ist ein Nachfahre ('descendant') von e_i. Ein Knoten ist sein eigener Vorfahre wie sein eigener Nachfahre.




4. Ein Knoten ohne einen Nachfolgerknoten ist ein Blatt ('leaf') (oder auch ein terminaler Knoten).




5. Knoten mit Nachfolgerknoten sind innere ('interior') Knoten.

Strukturtheorie

In der allgemeinen Strukturtheorie werden in Anlehnung an das Programm von BOURBAKI jene Strukturen formuliert, die als Basis für alle anderen speziellen Strukturen dienen.(irgendwann aufschreiben...)

Algebra

1. Verknüpfung: seien M₁, M₂, ...,M_n, M Mengen. Unter einer n-stelligen Verknüpfung versteht man eine Abbildng des kartesichen Produktes M₁ x M₂ x ... x M_n in die Menge M:
   f: M₁ x M₂ x ... x M_n ---> M
   Ist M₁ = M₂ = ... = M_n = M , so spricht man von einer inneren Verknüpfung. Besonders wichtig ist der Fall der zweistelligen (binären) Verknüpfung in einer Menge M.




2. Algebraische Struktur: eine Menge M, für deren Elemente mindestens eine Verknüpfung definiert ist, heisst Menge mit algebraischer Struktur. Algebraische Strukturen mit zwei zweistelligen inneren Verknüpfungen heisen auch Systeme mit doppelter Komposition. Bekannte Beispiele für algebraische Strukturen sind Gruppe, Ring, Verband.. Eine algebraische Struktur mit der Menge M und zwei Verknüpfungen wird z.B. geschrieben:

   <M,f₁,f₂ >



3. Ring R: eine algebraische Struktur mit zwei zweistelligen inneren Verknüpfungen (im allgemeinen Addition (Zeichen '+') und Multiplikation (Zeichen '*')) heisst ein Ring R, wenn für beliebige Elemente a,b,c ∈ R die folgenden Gesetze gelten:
   

   1. a + b = b + a (kommutatives Gesetz der Addition)

   
   

   2. (a + b) + c = a + (b + c) (assoziatives Gesetz der Addition)

   
   

   3. Zu je zwei Elementen a,b ∈ R gibt es genau ein Element x ∈ R mit a + x = b (Umkehrbarkeit der Assoziation)

   
   

   4. a * (b * c) = (a * b) * c (assoziatives Gesetz der Multiplikation)

   
   

   5. 1. a * (b + c) = a * b + a * c

      
      

      2. (b + c) * a = b * a + c * a (distributive Gesetze)

      
      
   
   

   6. Aus (i) - (v) folgt die Existenz genau eines Elementes 0 ∈ R mit der Eigenschaft a + 0 = a für alle a ∈ R. 0 heisst Nullelement (auch Einselement oder Neutrales Element) des Ringes

      .
   
   



4. Kommutativer Ring R: ein Ring R heisst kommutativ, wenn in ihm das kommutative Gesetz der Multiplikation gilt:
   a * b = b * a





5. Polynom in einer Unbestimmten über R: Sei R ein kommutativer Ring mit Einselement und x ein Rechensymbol, genannt Unbestimmte (Variable). Ein Ausdruck der Form

   
   f(x) = SUM(i=0; n) a_i * xⁱ = a_n * xⁿ + a_n-1 * x^n-1 + ... + a₁ * x + a₀
   
   

   mit a_i ∈ R heisst Polynom in einer Unbestimmten über R. Die a_i heissen Koeffizienten, a₀ heisst absolutes Glied des Polynoms. Falls a_n != 0 heisst n Grad des Polynoms und a_n Anfangskoeffizient oder höchster Koeffizient; ist a_n = 0 so heisst n formaler Grad von f(x). Polynome vom Grad 0,1,2,3 und 4 heissen auch konstant linear, quadratisch, kubisch bzw. biquadratisch.
   
   

6. Verband: eine algebraische Struktur V mit zwei 2-stelligen inneren Verknüpfungen (Zeichen: cut und u) heisst ein Verband, wenn für beliebige Elemente a,b,c in V gilt:

   
   
   (kommutative Gesetze)

   1. a cut b = b cut a

   
   

   2. a u b = b u a

   
   (assoziative Gesetze)

   3. a cut (b cut c) = (a cut b) cut c

   
   

   4. a u (b u c) = (a u b) u c

   
   (Absorptions- oder Verschmelzungsgesetze bzw. Dualgruppe)

   5. a cut (a u b) = a

   
   

   6. a u (a cut b) = a

   
   

   Jeder Verband (V; cut, u) kann als halbgeordnete Menge (V; <) aufgefasst werden. Die Ordnungsrelation ist gegeben durch

   a < b gdw a cut b = a




7. Komplement eines Verbandselementes: (V; cut, u) sei ein Verband mit Nullelement 0 und Einselement 1. Ein Element Ca in V heisst Komplement zu a in V gdw

   
   
   1. a cut Ca = 0
   
   
   2. a u Ca = 1
   
   




8. Komplementärer Verband: ein Verband heisst komplementär wenn er zu jedem Element mindestens ein Komplement enthält.





9. Distributiver Verband: ein Verband V heisst distributiv gdw ausser den Verbandsaxiomen noch die folgenden distributiven Gesetze gelten:

   
   

   1. a cut (b u c) = (a cut b) u (a cut c)

   
   

   2. a u (b cut c) = (a u b) cut (a u c)

   
   



10. 
    




11. Boolscher Verband (oder: Algebra): ist ein distributiver und komplementärer Verband. Ein Boolscher Verband A heisst normiert, wenn jedem Element a ∈ A eine Zahl p(a) zugeordnet werden kann, so dass die folgenden Bedingungen erfüllt sind:

    
    

    1. 0 < p(a) < 1

    
    

    2. p(0) = 0, p(1) = 1

    
    

    3. a < b ==> p(a)< p(b)

    
    

    4. a cut b = 0 ==> p(a u b) = p(a) + p(b)

    
    

    p(a) heisst die Norm von a. In der Wahrscheinlichkeitsrechnung wird der Boolsche Verband als Ereignisalgebra gedeutet; p(a) ist dann die Wahrscheinlichkeit von a.





12. Verallgemeinter Boolscher Verband (oder: Algebra): ist ein distributiver und relativkomplementärer Verband.

Masstheorie

Mit Begriffen wie Ring, sigma-vollständiger und delta-vollständiger Ring, Borel-Ring, Borel-Menge, allgemeiner Halbring mit einem Mass usf. Grndzüge der Masstheorie

Wahrscheinlichkeitstheorie

Ausgehend von Begriffen wie sigma-Algebra und Borel-Menge Grundzüge einer axiomatischen Wahrscheinlichkeitstheorie

Bayessche Netze

Optimierungstheorie

Maschinelles Lernen

Formale Sprachen

Im Kontext von formalen Sprachen werden endliche Mengen auch benutzt, um Alphabete zu repräsentieren.

1. Sei A solch ein Alphabet. Wenn x ∈ A dann heisst x gewöhnlich ein Zeichen ('letter') oder Symbol ('symbol').

2. Die Aneinanderfügung von Zeichen aus A ergibt eine Zeichenkette ('string') über A bzw. ein Wort ('word') über A.

3. A* ist die Menge aller Wörter über A (während A n.V. endlich ist gilt dies für A* nicht).

4. A* enthält auch das leere Wort, das wir durch '§' repräsentieren (in der Literatur meistens kleines Lambda oder kleines Epsilon). Damit wären '§', '01', '111', '101010' Worte über dem Alphabet A01' = {0,1}.

5. A⁺ = A* - {§}.

6. Eine Teilmenge von A* heisst eine (formale) Sprache. Daher gilt die leere Menge 0 wie auch die Menge mit dem leeren Wort {§} als eine Sprache. Im Gegensatz zur Sprache {§} enthält die Sprache 0 kein Element..

Mittels der Menge A* und der Operation Konkatenation 'o' lässt sich jetzt eine Struktur <A*, o > als Halbgruppe mit neutralem Element (Monoid) definieren, die folgende Eigenschaften haben soll:

Für alle x,y ∈ A* soll gelten:

7. x o y = xy in A* (Abgeschlossenheit)




8. (x o y ) o z = x o ( y o z ) = xyz (Assoziativität)




9. § o x = x o § = x (Neutrales Element)

Damit kann man vereinbaren: wenn w, u₁,u₂, v Worte über einem Alphabet A sind, dann gilt:

11. wⁿ = ww ...w (n-mal) (eine n-fache Konkatenation)

12. speziell gelte w⁰ = §.

13. |w| := Länge eines Wortes; Anzahl der Zeichen in dem Wort w, wobei jedes Zeichen sooft gezählt wird, wie es vorkommt; mit den zusätzlichen Eigenschaften:

14. |§| = 0

15. |u₁,u₂,| = |u₁|, + |u₂,|

16. |wⁿ| = n * |w|

17. v ist ein Teilwort von w wenn w = u₁vu₂. Wenn u₁ = § dann ist v ein Präfix, ist u₂ = § dann ist v ein Suffix. Jedes Wort w ist trivialerweise Teilwort, Präfix und Suffix von sich selbst; ebenso gilt dies für das leere Wort §.

18. Seien A,B Teilmengen von ALPH* mit ALPH als einem Alphabet, dann sind A und B Sprachen. folgende Begriffe werden benötigt:

    1. A u B = { x | x ∈ A oder x ∈ B }

    2. A cut B = { x | x ∈ A und x ∈ B }

    3. c(A) (auch Querstrich über A) = ALPH* - A

    4. AB = { xy | x ∈ A und y ∈ B }

    5. A⁰ = {§}

    6. A¹ = A

    7. Aⁿ⁺¹ = AAⁿ

    8. AⁱA^j=(Aⁱ)^+j

    9. A^* = U (n > 0) Aⁿ

    10. A⁺ = U (n > 1) Aⁿ

19. Seien R,S Relationen auf ALPH* mit ALPH als einem Alphabet, also R, S C ALPH* x ALPH*. Folgende Begriffe werden vereinbart:

    1. RS = { (x,y) | (E:z)( xRz und zSy ) }

    2. R⁰ = { (x,x) | (x ∈ ALPH* }

    3. R¹ = R

    4. Rⁿ⁺¹ = RRⁿ

    5. R^* = U (n > 0) Rⁿ

    6. R⁺ = U (n > 1) Rⁿ
       
       Aus diesen Definitionen folgt, dass xR*y gilt, falls x = y oder es gibt z₁,z₂ , ..., z_n mit n > 1, so dass gilt xRz₁, z₁Rz₂ , ..., z_nRy.

    7. Es gilt, dass R* die kleinste reflexive und transitive Relation ist, die R umfasst (die kleinste reflexive und transitive Hülle von R).

    
    

20. Die Sprache L ist durch eine Turingmaschine m entscheidbar (bzw. L ist rekursiv): RECURSIVE(L,m) gdw DTM(m) & (A:x)( INPU(x,m) ==> [x ∈ L & ACCEPT(x,m)] or [x ∉ L & REJECT(x,m)] ) )

    
    
    (Für Turingmaschine bzw. DTM siehe bei ->Automaten)




21. Die Sprache L ist durch eine Turingmaschine m semientscheidbar (bzw. L ist rekursiv aufzählbar/ turing-aufzählbar): RECURSIVE_ENUMERABLE(L,m) gdw DTM(m) & (A:x)( INPU(x,m) ==> [x ∈ L & ACCEPT(x,m)] or [x ∉ L & ¬ACCEPT(x,m)] ) )
    
    '¬ACFEPT(x,m)' schliesst ein, dass die Turingmaschine möglicherweise nicht anhält.





22. Es gilt, dass die Menge der rekursiven Sprachen eine echte Teilmenge der rekursiv-aufzählbaren Sprachen bildet.





23. Es gilt, dass das Komplement einer rekursiven Sprache auch rekursiv ist.





24. Es gilt, wenn sowohl eine Sprache L wie auch ihr Komplement rekursiv-aufzählbar ist, dann sind auch beide rekursiv (turing-entscheidbar).

Beispiele: die Menge der Theoreme und Nichttheoreme bei formalen Systemen. Wenn eine Zeichenkette w ein Theorem ist, dann gibt es dazu einen endlichen Beweis, der sich nach endlich vielen Schritten finden lässt; eine DTM angesetzt auf ein w als Theorem würde also nach endlich vielen Schritten stoppen. Wäre die Eingabe w ein Nichttheorem, dann gäbe es dazu keinen Beweis; die Suche nach einem solchen nichtvorhandenen Beweis müsste nicht nach endlich vielen Schritten stoppen. Verschiedene Versuche, 'entscheidbare Eigenschaften' von Nichttheoremen relativ zu einem bestimmten formalen System zu finden, waren für bestimmte Teilmengen von Nichttheoremen bislang erfolgreich, aber einer vollständigen Lösung widersetzt sich die Menge der Nichttheoreme bis heute hartnäckig (vgl. dazu auch [Döben 1990]).

Automaten

Im Grundlagenstreit um die Entscheidbarkeit mathematischer Theorien hatte sich gezeigt, dass eine Minimalvoraussetzung für eine befriedigende Diskussion um die Entscheidbarkeit darin bestand, dass die Beweisführung in einem endlichen Verfahren mit endlichen Mitteln stattzufinden habe. Anders formuliert heisst dies, dass solch ein effektives Verfahren intutiv die folgenden Eigenschaften besitzen sollte:

1. Das Verfahren als Ganzes muss mit endlichen Mitteln beschreibbar sein




2. Das Verfahren muss sich in einzelne, klar unterscheidbare Schritte zerlegen lassen




3. Jeder Schritt muss sich mechanisch ausführen lassen.

Dasjenige Verfahren, das diesen intuitiven Forderungen nach Auffassung von GÖDEL und CHURCH historisch als erstes am nächsten kam, war ein Verfahren von TURING aus dem Jahr 1936, das von CHURCH Turingmaschine genannt wurde. Wie sich im Laufe der Jahre zeigte, konnten bislang alle anderen Verfahren, die auch den Anspruch erhoben, ein effektives Verfahren zu sein, als mit der Turingmaschine äquivalent erwiesen werden. Wir beginnen daher die Darstellung der Automaten mit dem Konzept der Turingmaschine; andere Automatentypen folgen.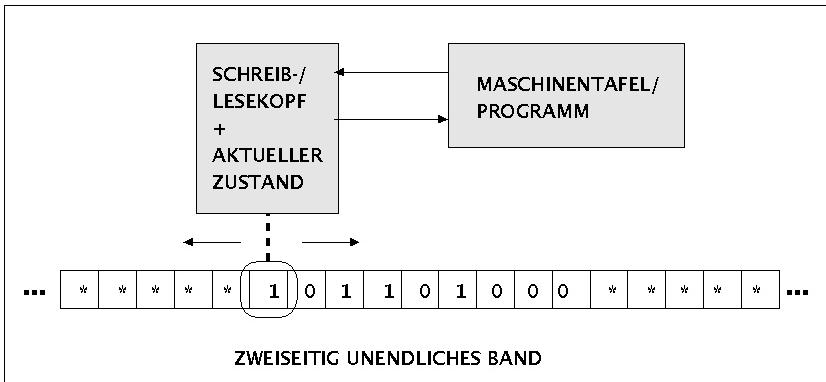

Deterministische 1-Band Turingmaschine

Wir wählen hier die Form der deterministischen Turingmaschine (DTM) mit einem Band.. Wie später gezeigt wird, sind andere Formen von Turingmaschinen (1/2-Band, mehrere Bänder, universelle Turingmaschine, nichtdeterministische Turingmaschine usw. nicht stärker als eine DTM).

Intuitiv besteht eine Turingmaschine aus einem nach beiden Seiten offenen Band ('tape'), das gleichmässig in rechteckige Felder ('squares') unterteilt ist. Zu Beginn einer Rechnung ist das Band leer bis auf eine endliche Menge von Symbolen I aus einem endlichen Alphabet A, die nacheinander auf das Band geschrieben sind, pro Feld ein Symbol. Alle anderen Felder enthalten das leere Zeichen '§', das nicht zum Alphabet A gehört (A - {§}) (In der Literatur gibt es eine Vielzahl von Konventionen zur Bezeichnung des leeren Feldes {'b', 'B', 'kleines Epsilon', 'leeres Quadrat, 'Unterstrich mit Winkeln nach oben', '*'}. Das Alphabet A ist nicht leer. Zu Beginn der Rechnung steht der Schreib-Lese-Kopf genau über dem ersten Feld der Inschrift I. Die Turingmaschine befindet sich im Start-Zustand q₀. Die Menge aller Zustände Q ist endlich. Neben dem Startzustand q₀ enthält sie noch eine endliche Menge von Endzuständen E = {q_e.1, ...,q_e.k } mit k > 1. Die Aktionen einer DTM sind in der Maschinentafel, dem 'Programm' der Turingmaschine, festgelegt. Eine Maschinentafel besteht aus einer endlichen nichtleeren Menge von Übergangsregeln D, wobei eine einzelne Übergangsregel d_i die Form hat:

1. q_i: wenn der aktuelle Zustand q_i ist




2. v_j: und das Zeichen, das aktuell vom Schreib-Lesekopf gelesen wird, v_j ist,




3. q'_i: dann soll der nächste Zustand q'_i sein,




4. v'_j: und als Zeichen soll auf das aktuelle Feld das Zeichen v'_j geschreieben werden




5. h_i: und der Schreib-Lesekopf soll in Richtung h_i bewegt werden.

v_j, v'_j sind aus G = A u {§} und
h_i ist aus {'L', 'R', 'S'}; es bedeutet 'L' := auf dem Band ein Feld nach 'links', 'R' := auf dem Band ein Feld nach 'rechts', 'S' := Stop, keine Bewegung mehr. Ein Zustand q_i als erstes Element einer Übergangsregel, bei dem als letztes Element ein Stop-Symbol 'S' steht, heisst ein Endzustand. Davon zu unterscheiden sind jene Zustände, die die Maschine stoppen unabhängig davon, welches Symbol gelesen wird und welche Richtung im letzten Element einer Übergangsregel angegeben ist.

Beginnend mit dem Startzustand q₀ auf dem ersten Zeichen einer Inschrift I wird eine DTM also einzelne Aktionen anhand der Menge der Übergangsregeln in der Maschinentafel ausführen. Grundsätzlich sind nun drei Fälle denkbar:

1. Eine DTM mit Argument I gerät in eine Endlosschleife




2. Eine DTM mit Argument I gerät nicht in eine Endlosschleife und hat nach n-vielen Aktionen gestoppt




3. Eine DTM mit Argument I gerät nicht in eine Endlosschleife aber hat nach n-vielen Aktionen noch nicht gestoppt

Tritt Fall (2) ein, dann soll die Konvention gelten, dass die DTM die ursprüngliche Eingabe I gelöscht hat und der Schreib-Lesekopf am Ende wieder auf dem ersten Zeichen des Ergebnisses steht; das Ergebnis kann leer sein.

Damit kann man nun folgende formalisierte Darstellung einer deterministischen Turingmaschine (DTM) geben:

mit

1. Q:= endliche nichtleere Menge von Zuständen




2. A:= endliches Alphabet (für Argumente und Werte); |A| > 0




3. G = A u {§}; das endliche Bandalphabet




4. § := das Leerzeichen




5. q₀ := der Anfangszustand; q₀ ∈ Q




6. E := Menge der Endzustände; E C Q & E != 0




7. D = {'L', 'R', 'S'}; endliche Menge von Richtungsaktionen ('links', 'rechts', 'stop')




8. d₀, ..,d_n := endliche Menge von Übergangsfunktionen; d_i: Q-E x G ---> Q x G x D




9. Maschinentafel/ Programm := die endliche Menge von Übergangsfunktionen d₀, ..,d_n einer Turingmaschine m heisst die 'Maschinentafel' oder das 'Programm' der DTM m.




10. k ist eine Konfiguration einer Turingmaschine m: CONFIGURATION(k,m) gdw m ist eine determinstische Turingmaschine & k ist eine Zeichenkette 'aqb' mit a,b aus G*_m und q aus Q_m. Auf dem Band befindet sich die Inschrift I = ab, eingerahmt von Blanks, und der Schreiblesekopf im Zustand q steht auf dem ersten Zeichen von b. Folgende Fälle sind hier zu unterscheiden:

    1. q ist der Startzustand q₀ und a ist leer; dies nennen wir eine Startkonfiguration ('START_CONFIGURATION') und b die Eingabe der Turingmaschine;
    
    
    
    2. q ist ein Endzustand und a ist wiederum leer (zum Ende steht immer nur das Ergebnis auf dem Band), also q_endb; dies nennen wir auch eine Endkonfiguration ('END_CONFIGURATION') und b das Ergebnis;
    
    
    
    3. q ist weder Start- noch Endzustand.
    
    
    

11. Die Menge der Konfigurationen ('configurations') einer Turingmaschine m: configurations(m) = { k | CONFIGURATION(k,m) }





12. Direkte Nachfolgekonfiguration einer Turingmaschine m: eine 'direkte Nachfolgekonfiguration' von aqb ist die Zeichenkette a'q'b', wenn a'q'b' aus aqb durch Anwendung einer Übergangsregel d_i entstanden ist. Man schreibt:
    
    

    aqb |--_m a'q'b'




13. P ist ein Protokoll ('protocol') mit der Länge n von der Turingmaschine m für die Eingabe x : PROTOCOL(P,m,x,n) gdw P ist ein Tupel der Länge n & rn(P) C configurations(m) & (A:i)( i ∈ dm(P) ==> k_i |-- k_i+1 mit i < n )





14. k' ist die Nachfolgekonfiguration von k bei einer Turingmaschine m oder k' ist ableitbar von k mit einer Turingmaschine m: ABL(k',k,m) gdw (E:P,n)( PROTOCOL(P,m,k,n) & END_CONFIGURATION(k',m) & k' = P_n. Statt ABL(k',k,m) schreibt man auch:
    
    

    k |*--_m k'




15. n ist die Länge ('length') einer Ableitung einer Turingmaschine m für die Eingabe k: k |*--_m k' ==> lenth(k,k',m) = n gdw (E:P) PROTOCOL(P,m,k,n)





16. Der INPUT x einer Turingmaschine m: INPUT(x,m) gdw TM(m) & '§q₀x' ist eine Startkonfiguration von m





17. Rechenzeit: die Rechenzeit einer DTM ist die Zahl der Zustandsübergänge, bis die TM, angesetzt auf die Eingabe k mit dem Ergebnis k' stoppt. Da jeder endlichen Berechnung eine Ableitung korrespondiert, kann man auch sagen, die Rechenzeit entspricht der Länge der Ableitung von k' aus k unter m.





18. Die Eingabe x wird von einer Turingmaschine m akzeptiert ('accepted'): ACCEPT(x,m) gdw DTM(m) & §q₀x |*-- §q'1 & q' ∈ E





19. Die Eingabe x wird von einer Turingmaschine m nicht akzeptiert ('rejected'): REJECT(x,m) gdw DTM(m) & §q₀x |*-- §q'0 & q' ∈ E





20. Die von einer Turingmaschine m erkannte Sprache L: L(m) = { x | TM(m) & ACCEPT(x,m) }





21. Simulation: Ein Automat M' simuliert einen Automat M gdw für jedes Argument w mit M(w) = w' gilt M'(w) = w'. Damit ist vereinbar, dass der Platz- und/oder Zeitbedarf von M' grösser oder kleiner ist als von M (so gilt z.B., dass eine Registermaschine (s.u.) sich von einer der Varianten der Turingmaschine im Zeitverbrauch maximal um einen polynomialen Faktorunterscheidet).

Im Rahmen der Komplexitätstheorie (s.u.) wird die deterministische Turingmaschine (DTM) benutzt, um die Komplexitätsklasse P zu definieren. Zur Definition der Komplexitätsklasse NP benötigt man eine andere Variante der Turingmaschine, nämlich eine nichtdeterministische Turingmaschine (NDTM). Nichtdeterministische Turingmachinen zeichnen sich dadurch aus, dass sie in jedem Zustand nicht nur genau eine Fortsetzung kennen, sondern u.U. mehr als eine. Man kann dies entweder so realisieren, dass man die Übergangsfunktion entsprechend abändert oder aber, und das ist die Variante die hier benutzt werden wird, man ergänzt eine DTM um ein 'Schätzmodul' ('guessing module').

Nichtdeterministische 1-Band Turingmaschine (NDTM)

Die Arbeitsweise der NDTM unterscheidet sich von der Arbeitsweise der DTM nur darin, dass vor (!) Beginn eines Protokolls, nachdem (!) der INPUT der NDTM schon auf das Band geschrieben wurde, das Schätzmodul 'links' vom INPUT eine 'Schätzung' hinschreiben kann; diese Schätzung kann beliebig lang sein; das Hinschreiben muss nicht stoppen. Sollte das Schätzmodul seine Arbeit einstellen, dann beginnt jener Teil der NDTM, der mit einer DTM identisch ist, seine Arbeit. Dies bedeutet, dass der deterministische Teil als Eingabe entweder eine konktrete Schätzung vorliegen hat oder nicht.

Damit kann man nun folgende formalisierte Darstellung einer nichtdeterministischen Turingmaschine (NDTM) geben:

mit

1. Q:= endliche nichtleere Menge von Zuständen




2. A:= endliches Alphabet (für Argumente und Werte); |A| > 0




3. G = A u {§}; das endliche Bandalphabet




4. § := das Leerzeichen




5. q_g.0, q_g.1, ..., q_g.k, q₀ := diverse Schätzzustände und der Anfangszustand q₀ ; { q_g.0, q_g.1, ..., q_g.k, q₀} C Q




6. E := Menge der Endzustände; {q_Y, q_N } C E C Q; q_Y steht für Akzeptanz und q_N für Ablehnung




7. D = {'L', 'R', 'S'}; endliche Menge von Richtungsaktionen ('links', 'rechts', 'stop')




8. d* := spezielle Übergangsfunktion des Schätzmoduls; d*: {q_g.0, q_g.1, ..., q_g.k} x G ---> {q_g.0, q_g.1, ..., q_g.k, q₀} x G x D

   
   



9. d₀, ..,d_n := endliche Menge von Übergangsfunktionen; d_i: Q-(E u {q_g.i} ) x G ---> Q -{q_g.i} x G x D




10. Maschinentafel/ Programm := die endliche Menge von Übergangsfunktionen d₀, ..,d_n einer Turingmaschine m heisst die 'Maschinentafel' oder das 'Programm' der NDTM m. Die spezielle Übergangsfunktion d* definiert eine Menge konkreter Schätzregel, die zusammen ein Schätzprogramm bilden.




Die weiteren Begriffe (s.o.) sind weitgehend identisch mit dem Fall der (D)TM.

11. Die Eingabe x wird von einer nichtdeterministischen Turingmaschine m akzeptiert ('accepted'): ACCEPT(x,m) gdw NDTM(m) & §q₀x |*-- §q_Y
    
    

12. Die Eingabe x wird von einer nichtdeterministischen Turingmaschine m abgelehnt ('rejected'): REJECT(x,m) gdw NDTM(m) & §q₀x |*-- §q_N





13. Eine nichtakzeptierende Berechnung einer nichtdeterministischen Turingmaschine m : NONACCEPTING(x,m) gdw NDTM(m) & REJECT(x,m) or ¬(E:P,k) PROTOCOL(P,m,x,k)





Zu einem INPUT x für eine NDTM m kann es -in Abhängigkeit von den unendliche viele Schätzungen- entsprechend viele Rechnungen geben.Ein INPUT x soll als akzeptiert gelten, wenn es wenigstens eine Schätzung gibt, bei der gilt: ACCEPT(x,m)




14. Die von einer nichtdeterministischen Turingmaschine m erkannte Sprache L: L(m) = { x | NDTM(m) & ACCEPT(x,m)}

Komplexitätstheorie

In der Komplexitätstheorie wird die 'Komplexität' ('complexity') eines Problems gemessen am Ressourcenbedarf für seine Repräsentation und für seine Lösung. Neben der Ressource 'Platz' ('space') ist es vor allem der 'Zeitbedarf' ('time'), der zur Charakterisierung benutzt wird.

1. Problem: Ausgangspunkt ist immer ein 'Problem', dessen Komplexität bestimmt werden muss. Dieses Problem ist sprachlich, d.h. in Form einer Zeichenkette ('string') über einem endlichen Alphabet A zu repräsentieren. Der Vorgang der 'Übersetzung' der nichtsprachlichen Fassung des Problems in eine sprachliche Fassung heisst 'Enkodierung' und die Gesamtheit der Regeln, die eine Enkodierung steuern, heisst auch 'Enkodierungsschema'. Teile der Zeichenkette, in die ein Problem enkodiert wird, sind freie Variablen (die 'Parameter' des Problems), die für mögliche Werte stehen. Ferner muss beschrieben werden, welche Eigenschaften eine 'Lösung' ('solution') aufweisen soll.




2. Instanz: Eine 'Instanz' eines 'Problems' erhält man, indem man für die Variablen des Problems konkrete Werte einsetzt. Die Anzahl der Zeichen in der Zeichenkette, die die Instanz repräsentiert, ist zugleich die Länge des Inputs für den Lösungsalgorithmus.




3. Bsp: Reisender ('traveling salesman'): Die Parameter dieses Problems sind eine endliche Menge von Städtenamen NAMEN = { n₁, ..., n_m } und der Abstand zwischen je zwei Städten d(n_i,n_j). Eine Lösung wäre eine Anordnung o der Städte < n_o.1, ..., n_o.m > so dass der Gesamtweg y minimal ist:
   
   y = min([SUM(j=1, m-1) d(n_o.j,n_o.j+1)] + d(n_o.m,o.m+1_j))
   
   In der obigen Formel bekommt man die Länge der gesamten Tour beginnend bei o.1, endend bei o.m und dann wieder o.1.




4. Algorithmus/ Programm: Die Lösung soll durch einen 'Algorithmus' geleistet werden. Wie aus der theortischen Informatik bekannt, ist der Begriff des Algorithmus äquivalent zu 'Programm', 'Sprache', 'Grammatik', 'Automat' und 'Funktion'. Ein Algorithmus löst ein Problem P genau dann, wenn er für jede Instanz des Problems P immer die gewünschte Lösung in endlich vielen Schritten generiert.




5. Effizienz: Ein 'effizienter' Algorithmus impliziert im allgemeinsten Sinne natürlich alle Ressourcen, die notwendig sind, um ein Problem zu lösen (Raum, Zeit, Hardware, Strom...). Im folgenden fokussieren sich die Betrachtungen auf den Zeitbedarf, da dieser aus Anwendungsrücksicht die dominante Eigenschaft ist.

6. Rechenzeit: Worst-Case Rechenzeit bezieht sich auf das Maximum über alle Rechenzeiten aller Eingaben aus einer endlichen Menge M; Average-Case Rechenzeit ist der Erwartungswert der Rechenzeit bzgl. einer Wahrscheinlichkeitsverteilung p auf einer Menge M von Eingaben. In der Praxis ist die Average-Case Rechenzeit oft schon bei einfachen Beispiel nicht berechenbar; zudem fehlen auch meist Hinweise auf die anzunehmende Verteilung p.

7. Zeit-Komplexitäts-Funktion ('time complexity function'): diejenige Funktion, mit der man, abhängig von der Länge des Inputs zu einem Algorithmus, den maximalen Zeitbedarf errechnet, den der Algorithmus benötigt, um die Lösung auszugeben, z.B.:
   
   maxtime_M: A^*_E ---> Nat'
   
   Die genaue Definition einer Funktion 'maxtime' hängt ab von dem Maschinenmodell M, auf dem man den Algorithmus ausführt, sowie von dem verwendeten Enkodierungsschema E, mit dem man das Problem P in eine Menge von Zeichenketten über dem endlichen alphabet A enkodiert. Da sicht zeigt, dass die Wahl von M und E sich höchstens polynomial voneinander unterscheiden, genügt es im allgemeinen, die Parameter M und E offen zu lassen; jeder kann sich hier das Maschinenmodell und das Enkodierungsschema seiner Wahl 'vorstellen'.

8. O-Notation: Zur Charakterisierung der Komplexität von Algorithmen hat sich die sogenannte 'O-Notation' eingebürgert. Hier einige wichtige Definitionen (siehe dazu z.B. [NIEVERGELT 1997:337ff]):

   Sei Rel⁺ die Menge der nichtnegativen reellen Zahlen und f eine Funktion f:Rel⁺ ---> Rel⁺

   • o(g) "Klein oh": o(g) = { f:Rel⁺ ---> Rel⁺ | lim(f(x)/g(x) = 0 für x -> infinite }
     
     /* f wächst langsamer als g */

     
     
     

   • O() "Gross Oh": O(g) = { f:Rel⁺ ---> Rel⁺ | (E:c,y)(A:x)( c > 0 & y ∈ Rel⁺ & x > y & f(x) < c * g(x) }
     
     /* f wächst höchstens so schnell wie g */
     
     

   • OMG() "Omega": OMG(g) = { f:Rel⁺ ---> Rel⁺ | (E:c,y)(A:x)( c > 0 & y ∈ Rel⁺ & x > y & f(x) > c * g(x) }
     
     /* f wächst mindestens so schnell wie g */
     
     

   • THET() "Theta": THET(g) = O(g) cut OMG(g)
     
     /* f wächst gleich schnell wie g */
     
     

9. Polynomialer Zeitalgorithmus ('polynomial time algorithmus'): Ein polynomialer Zeitalgorithmus ist ein solcher bei dem die Zeitkomplexitätsfunktion gegeben ist als O(p(n)) mit p als einer polynomialen Funktion und mit n als Inputlänge. Aufgrund 'praktischer Erfahrungen' (!) hat sich gezeigt, dass ein Kriterium für 'effiziente' bzw. 'ineffiziente' Algorithmen darin besteht, dass ein Algorithmus die Lösung in polynomer bzw. in exponentieller Zeit findet. Im Fall effizienter Algorithmen soll zusätzlich gelten, dass die Länge der Lösung beschränkt ist auf eine polynomiale Funktion der Eingabelänge.

In der nachfolgende Tabelle sieht man eine Beispielmaschine für die Inputlängen n=10 ... 60 mit unterschiedlichem polynomem oder exponentiellem Zeitbedarf: