by
Dr. Gerd Döben-Henisch
INM - Institut for New Media
andinm numerical magic gmbh
Daimlerstr. 32
D-60314 Frankfurt am Main
Tel: 069-941 963-10
Fax: 069-941 963-22
email: doeb@inm.de
This paper demonstrates a basic equation between 'semiotics' and 'computational semiotics'. The term 'semiotics' is here understood according to the writings of Charles Morris, and the term 'computational' is based on the concept of the 'Turing machine' as provided by Alan Matthew Turing. Taking the concept of a 'scientific theory' as the common point of reference, it is shown how the concept of the Turing machine and the concept of semiotics can be reconstructed uniformly within this framework. Finally, it is shown how one can construct a mapping between the concept of 'semiotic agent' as proposed by Morris and the concept of the Turing machine. The result is that everything that can be said about a semiotic agent within Morris's concept of semiotics can be stated in terms of the Turing machine concept.
Connecting Alan Matthew Turing (1912-1954), the great British mathematician and logician, with semiotics is not a straightforward task.
Turing himself never mentioned semiotics explicitly and he never called himself in any sense a 'semiotician', nor did any of his colleagues thus identify him, nor any writer after his death.
Turing was an outstanding researcher active mainly in the field of mathematics, meta-mathematics, and logic, with a period of intensive work with calculating machines, and then, later on, with groundbreaking work in theoretical chemistry and in the philosophy of artificial machines. But not in semiotics (cf. Hodges 1988, 1994)

Despite this lack of an explicit historical relationship between Turing and semiotics, one can nevertheless show that such a relationship exists. Moreover, from the present vantage point, one would be inclined to say that Turing's contribution to semiotics is very fundamental indeed, if not the most fundamental to the history of semiotics.
To understand Turing's importance to semiotics, one must step back a bit and look at the larger perspective through the fields of meta-mathematics, computational machines, theory of science, semiotics and modern engineering.
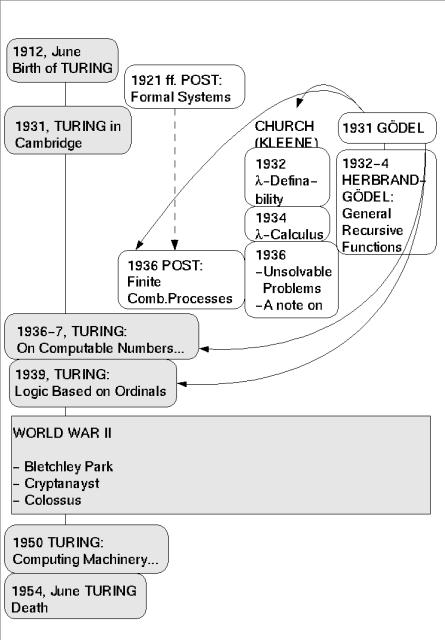
During his short life, Turing wrote many important papers (cf. the list of Turing's publications in References). But the one most relevant here is "On Computable Numbers, with an Application to the Entscheidungsproblem [decision problem]", written in 1936 and published at the turn of 1936-37. In this paper he solved this long-debated problem of meta-mathematics. Although he was not the only one to publish papers on this topic in these years (cf. the diagram: 'TURINGSLIFE'), and although his solution was preceded by a similar result achieved by Alonzo Church (Church 1936, 1936a), it was Turing's paper that became most widely accepted and which was the starting point for the famous 'Turing Machine' concept, a name introduced by Alonzo Church in his review of Turing's paper in the Journal of Symbolic Logic, 1937.
While Gödel was not convinced by Church's proof of 1936, he immediately accepted Turing's paper, and in his remark at Princeton in 1946 he stated that 'with this concept [i.e. Turing's computability], one has for the first time succeeded in giving an absolute definition of an interesting epistemological notion, i.e., one not dependent upon the formalism chosen' (cited in Davis 1965:83). And even Church was willing to accept Turing's conceptual approach as convincing when, in his review of Turing, he stated: "Of these methods [Turing's computability, general recursiveness, and lambda-definability], the first has the advantage of making evident immediately the identification effective in the ordinary (not explicitly defined) sense - i.e. without the necessity of proving preliminary theorems. The second and third have the advantage of being suitable for being incorporated within a system of symbolic logic.' (cf. Church 1937).
To understand the importance of Turing's paper, in particular, one must consider for a moment the essence of the 'Entscheidungsproblem', which was so prominent at that time.
At the turn of the 19th and in the first quarter of the 20th century, meta-mathematics (theorizing about mathematics) reached a new peak: the formalization of logic attained a new maturity which allowed mathematicians increasingly to formalize their thinking about mathematics and not just mathematics itself. And it was 'proof theory' which most profited from this development.
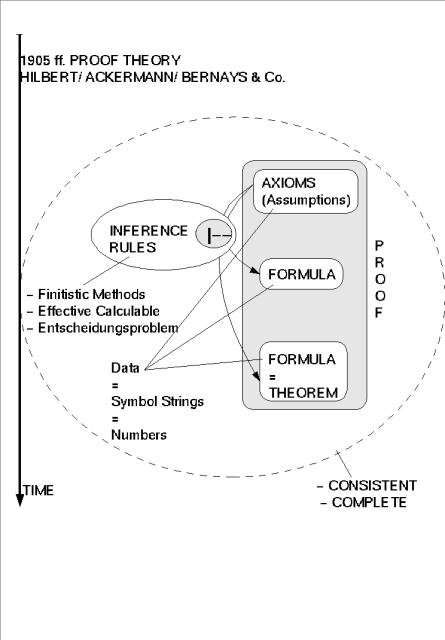
In proof theory (cf. the diagram 'HILBERT&CO) one investigates the method of arriving at a new true statement from a set of existing true statements (called 'axioms' and 'assumptions') and also at a set of rules that indicate how to generate ('infer') new true statements from previous ones. Any such sequence of assumptions and rule-generated new statements is called - with regard to the last statement generated - a proof. The generating rules are called 'inference rules', and a system of inference rules is called a logic.
In reference to this framework, one can characterize the Entscheidungsproblem as follows: Given a collection of assumptions A stated in some logical system, and a statement S, is it possible to decide on the basis of some universal computation method whether S can or cannot be inferred from A? If such a universal computational method existed, then could such a method be called a 'decision method' for this logic. For logical systems that are weaker than 'first-order logic', several such procedures existed before Church's and Turing's publications, but not for systems of logic that are at least as strong as first-order logic (cf. Kneale, William/ Kneale, Martha 1962:724-737).
At that time, it was generally held that the whole process of generating a proof should be 'finitistic'. But there was no common agreement about the properties which would necessarily constitute a finitistic method. Mathematicians considered arithmetic to be an example of finitistic method. Other methods considered to be similar to the finitistic were Post's formal systems (beginning in the 1920s), Church's lambda-calculus (together with Kleene) (1932-36), and Herbrand-Gödel's General Recursive Functions (1934).
All of these systems (except Post's) themselves relied on complex concepts dependent on external explanations and whose finitistic character was not established beyond doubt.
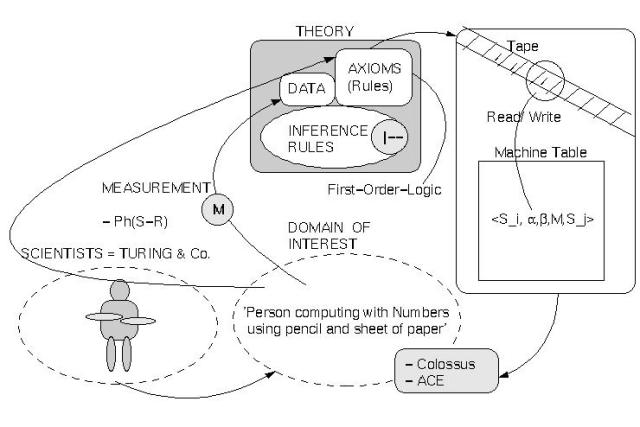
Under these circumstances, the advent of Turing's computational device, later called a 'Turing machine', was a major event. Unlike all others, but similar in some respects to Post, Turing primarily analyzed the pragmatic conditions under which a computing person calculates with numbers. His analysis ( cf. the diagram 'TURINGMACHINE') revealed as minimal structure (i) a tape with rectangular cells which can be filled with symbols, representing the sheets of paper of a computing agent, (ii) a machine with a finite number of conditions {q1, ..., qn} representing the computing agent and (iii) a relation between the tape and the machine based on the fact that 'at any given moment' only one square of the tape is 'in the machine'; the content of this square can be 'read' or can be 'written', and the tape can be 'moved' by one square in one of two directions. Which symbol would be written at any given moment and what move would occur depend solely on the state the machine is 'actually in' (cf. Turing 1936-37:117, citation according to the reprint in Davis 1965).
With these minimal elements of a symbol-processing system, Turing moved ahead of all that meta-mathematics had done so far: he no longer spoke solely about the formal expressions of a given system and their properties related to certain complex procedures of logical inference. Instead, he also took into account the operating logician or mathematician himself together with his pragmatic relationship to the symbolic expressions with which he was dealing in a specific case.
Clearly, Turing himself originally had in mind only a person dealing with numbers, but his model has far broader applications. A symbol on the tape can represent anything - any segment of reality - including properties of the computing agent himself; and the finite states within the machine can also represent any variety of state, e.g., physiological states within a biological system or subjective states within a phenomenologically described reality. Within these general parameters, Turing's minimal computing structure constitutes a very general pragmatic agent model. And it is this aspect of Turing's approach that made his arguments more convincing than any others.
Under the operating conditions obtaining for any symbol-processing agent (in philosophical terms this could be called a 'transcendental argument' in a Kantian sense), Turing is not obliged to use complex symbolic expressions stemming from other sources (as in the case of Church, Kleene, Herbrand or Gödel). He has only to rely on this minimal operating-agent structure, and anything more complex must be shown to be reconstructable from these a priori conditions. Turing's model implies that any symbol-processing agent can be formed within the framework of his assumptions. And insofar as one can assume that the physiological states of the human body (including the brain!) are conceivable as a finite set of states - not yet proved in sensu stricto - then Turing's model would also claim to cover the instance of human agents. Thus Turing's approach is very broad, and it is hard to conceive of an agent to be 'configured' whose behavior could not be covered by Turing's model. (A widespread argument challenging the explicatory power of Turing's model uses the opposing concepts 'discrete' and 'continuous', stating that continuous processes exist which cannot be comprehended within a discrete machine. But the property of the 'continuousness' of a process depends entirely on the way the process is observed and described; and it is impossible - at least in principle - to exclude the possibility of lowering the level of detail to a point at which any 'continuous' process is made up of a number of elementary parts interacting in a certain manner. Thus the opposition of 'discrete' and 'continuous' may amount to a mere artificial product of thinking and not a 'real' property of 'nature', in which case Turing's argument is not necessarily refuted.)
How can we relate Turing's concept of computability, his 'Turing machine', to semiotics?
Is there a relationship of any kind?
To establish such a relationship between Turing's thinking and semiotics, one must first have a sufficiently clear concept of semiotics. But there is no clear-cut definition of semiotics. Clearly, semiotics refers primarily to some concept of a symbol or sign combined with methods on how to work with this concept. But up until now (cf., e.g., the excellent handbook of Nöth [1985]), we have a great wealth of ideas and concepts related to semiotics but no clear-cut and commonly accepted theory. Thus speaking about semiotics implies some ambiguity, and the position an author ultimately assumes will inevitably be determined by his own preferences.
This author strongly prefers to employ modern prerequisites for scientific theory as a conceptual framework for the discussion. And to support this 'bias', he prefers using the writings of Charles Morris (1901-1979) as a main point of reference for discussion of the connection between Turing and semiotics. No exclusion of other 'great fathers' of modern semiotics is intended (Peirce 1839-1914, but also de Saussure 1857-1913, von Uexküll 1864-1944, Cassirer 1874-1945, Bühler 1879-1963, and Hjelmslev 1899-1965, to mention only the most prominent). But Morris seems to be the best starting point for the discussion because his proximity to the modern concept of science makes him a sort of bridge between modern science and the field of semiotics.
To make explicit whether Turing has contributed to semiotics, and in which senses this contribution might be of importance, we must first offer a short description of semiotics in regard to the writings of Morris. But before doing so, we must introduce the concept of a scientific theory as the framework for our preparation for an encounter between Turing's concept of computability and Morris' concept of semiotics.

At the time of the Foundations in 1938, his first major work after his dissertation of 1925, Morris was already strongly linked to the new movement of a 'science of the sciences', which was the focus of several groups connected to the Vienna Circle, to the Society of the History of the Sciences, to several journals and conferences and congresses on the theme, and especially to the project of an Encyclopedia of the Unified Sciences (cf., e.g., Morris, Charles W. [1936]) ()see the diagram 'MORRISLIFE').
In the Foundations he states clearly that semiotics should be a science, distinguishable as pure and descriptive semiotics (cf. Morris 1977: 17, 23), and that semiotics could be presented as a deductive system (cf. Morris 1977: 23). The same statements appear in his other major book about semiotics (Morris 1946), in which he specifically declares that the main purpose of the book is to establish semiotics as a scientific theory (M. 1946:28). He makes many other statements in the same vein.
At the time of Morris's writings, the philosophy of science was dominated by what was later called the 'received view' (for a good summary of the main lines of the discussion up to 1967, see Suppe, 1977), which was propagated primarily by Rudolf Carnap.
Rooted in Machean neo-positivism with sensations viewed as data, and combined with the conventionalism of Poincaré, the key idea of the 'received view' was that a scientific theory must use mathematics - or formal logic - as its general language for the stating of onsistencies and general laws, but that the terms of this mathematical language must be interpreted by a clearly defined observational language, the descriptive terms of which are to be based exclusively on observable phenomena (cf. Suppe 1977:50ff).
During the 1950s and 1960s it became clear that this concept was unsatisfactory. One of the main reasons for this was the fact that the theoretical terms can at best be only partially interpreted by the observational language. After the historic conference in Urbana, Illinois, in March 1969, enthusiasm for the theoretical debates of philosophy of science cooled a bit, and right up to the present day there is no new single unifying notion on the form a scientific theory should take.
For my proposal I will adopt ideas from the theory-concept urged by the theoretical physicist Ludwig (1978, 1978b), by the structuralist view as explained by Wolfgang Balzer (1982) as well as in Balzer, Moulines, and Sneed (1987), and by the meta-theoretical clarifications of Peter Hinst (1996). All these positions are rooted in the structural concept of Bourbaki (1970). To distinguish my proposal from the ones cited, I term my concept minimal theoretical framework (MTF). The intention of the MTF is to allow as many instances of scientific activity as possible to be subsumed under this framework, including semiotics.
The disposition of the MTF here will be somewhat informal, a rigorous treatment being beyond the scope of this paper.
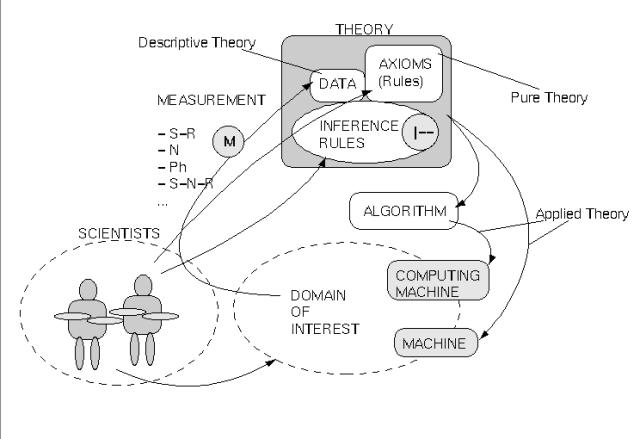
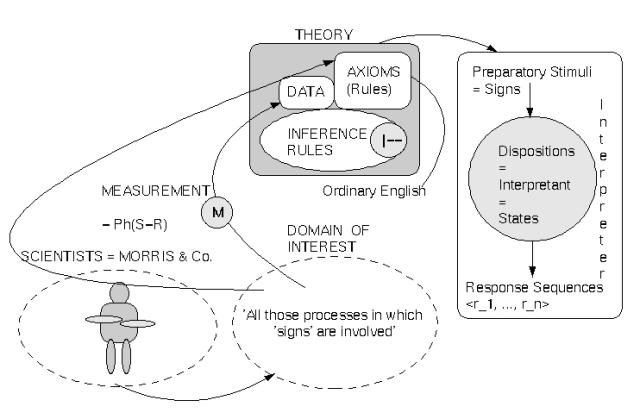
The starting point for any type of scientific exploration ( see diagram 'SCIENTIFIC') is the group of researchers, e.g., semioticians or researchers interested in computational semiotics (CS). That group is able to communicate in a primary language L0 (e.g. 'natural' English), which is embedded in a communicative context.
This group has a pre-scientific view of their subject of investigation. (In the case of CS, this view is given through 'candidates for semiotic processes‘.)
The group is able to define in their primary language certain methods of measurement. Depending on which 'point of view' one takes to view the 'world' one can distinguish several main 'types of measurement‘:
These measurements define the data. The data must be represented in some formal representation, a data representation language L1.
Furthermore, the group must have some axioms (rules) articulated in a theory language L2 to represent certain assumed regularities/ patterns/ consistencies in the realm of the data. L1 could be a subset of L2.
And finally, the group must have some meta-rules describing operations on data and axioms that permit logical inferences. These rules are called inference rules and are constituting a logical inference concept.
The formal structures representing the theory are intended to 'grasp‘ the 'empirical content‘ of the subject through formal means. In any case, this will be a form of approximation. The whole unit of data and axioms we call a theory.
It is possible, but not necessary, to set up an additional formal structure with the aid of an additional formal language L3 to encode the intended meaning of the theory in a model-theoretic manner.
As in many cases today, a computational model of the theory will be necessary. One reason is the complexity of the subject, especially if it has dynamic features. It is nearly impossible for a human brain to handle complex dynamic structures effectively. In order to claim those computational models as 'scientific‘ with regard to the presupposed theory, one must establish a mapping function between theory and the computational model. Insofar as such a mapping function exists, one can use the computational model to emulate the theory within this computational model and thereby simulate certain features of 'reality' if the main theory is an empirical theory. In case of engineering one constructs also machines based on a theory but these machines are not necessarily 'computational' machines in the sense of Turing.
A theory without data would amount to a purely formal structure and would thus be called a pure theory (in this sense any mathematical structure would be considered as a pure theory). With (empirical) data at hand, a pure theory becomes a descriptive or interpretive theory. This is what science usually intends to be. And a theory connected with a (computational) machine is called an applied theory.
With this concept of a scientific theory at hand, we will reconstruct Turing's contribution within this framework as well as the position of Morris. And we shall see that this will enable us to evaluate the semiotic relevance of Turing's contribution.
In Turing's case, one can quite straightforwardly relate his paper of 1936-7 to the concept of a scientific theory (see diagram: 'TURINGMACHINE').
The group of researchers is represented by Turing himself and by the people with whom he was communicating his ideas. The focus of investigation is given by real persons doing real computing work - writing numbers on sheets of paper with pencils. The modes of measurement have been restricted to normal perception; i.e., the subjective (= phenomenological) experience of an intersubjective situation and the symbolic representation has been done in ordinary English (=L1) as well as in a first-order language (=L1). But Turing was not primarily interested in the construction of a descriptive theory but in the elaboration of a formal structure that represents all the features of the subject of investigation that 'are of importance'. He represented this formal structure in a first-order theory (=L2) which can/must be understood rather as a pure theory than as an elaborated descriptive theory. Nevertheless, it is very simple to convert his pure theory in many instances into an interpreted theory.
The 'content' of his pure theory can be described as follows (cf. also above): there is (i) a tape with rectangular cells representing the sheets of paper of a computing agent which can be filled with symbols, (ii) a machine with a finite number of states {q1, ..., qn} representing the computing agent and (iii) a connection between the tape and the machine that is based on the fact that 'at any moment' only one square of the tape is 'in the machine', and the content of this square can be 'read' and can be 'written'; and the tape can be 'moved' by one square in one of two directions. Which symbol would be written at any moment and what move would occur depends solely on the state the machine is 'actually in' (cf. Turing 1936-37:117, citation according to the reprint in Davis 1965). The expression 'q_r = <S_i, a,b, M,S_j>' can be read as follows: the state 'q_r' is given by the quintupel '<S_i, a,b, M,S_j>' and 'S_i' is the identifying number of the state q_r, ' a' is the symbol just read on the actual square of the tape, ' b' is the symbol which has to be written on the actual square of the tape, 'M' is the next move on the tape ('left', 'right', 'halt'), and 'S_j' is the number of the next state which has to be entered.
Turing was also fortunate in being one of the first people to work on 'real' embodiments of this very general concept in that during World War II he was involved in the development of the Colossus computing machine. After the war, he also headed the ACE project (Automatic Calculating Engine) at the National Physics Laboratory (NPL) for some time. It remains an open question how far the North American projects (von Neumann and others) have been influenced by Turing's concept: his paper was well known there, and it was much broader in scope than the one that was used in the very limited ENIAC computer. Thus Turing's pure theory was gradually becoming also an applied theory.
To reconstruct the contribution of Charles Morris within the theory concept is not as straightforward as one might think. Despite his very active involvement in the new science-of-the-sciences movement (cf. diagram 'MORRISLIFE'), and despite his repeated claims to handle semiotics scientifically, Morris did not provide any formal account of his semiotic theory. He never left the level of ordinary English as the language of representation. Moreover, he published several versions of a theory of signs which overlap extensively but which are not, in fact, entirely consistent with one another.
Thus to speak about 'the' Morris theory would require an exhaustive process of reconstruction, the outcome of which might be a theory that would claim to represent the 'essentials' of Morris's position. Such a reconstruction is beyond the scope of this paper. Instead, I will rely on my reconstruction of Morris's Foundations of 1938 (cf. Döben-Henisch 1998) and on his basic methodological considerations in the first chapter of his 'Signs, Language, and Behavior' of 1946 (for the following see diagram[s]) (cf. diagram 'MORRIS´s Interpreter').
As the group of researchers, we assume Morris and the people he is communicating with.
As the domain of investigation, Morris names all those processes in which 'signs' are involved. And in his pre-scientific view of what must be understood as a sign, he introduces several basic terms simultaneously. The primary objects are distinguishable organisms which can act as interpreters [I]. An organism can act as an interpreter if it has internal states called dispositions [IS] which can be changed in reaction to certain stimuli. A stimulus [S] is any kind of physical energy which can influence the inner states of an organism. A preparatory-stimulus [PS] influences a response to some other stimulus. The source of a stimulus is the stimulus-object [SO]. The response [R] of an organism is any kind of observable muscular or glandular action. Responses can form a response-sequence [<r_1, ..., r_n>], whereby every singly intervening response r_i is triggered by its specific supporting stimulus. The stimulus-object of the first response in a chain of responses is the start object, and the stimulus-object of the last response in a chain of responses is the goal object. All response-sequences with similar start objects and similar goal objects constitute a behavior-family [SR-FAM]. Based on these preliminary terms he then defines the characteristics of a sign [SGN] as follows: 'If anything, A, is a preparatory-stimulus which in the absence of stimulus-objects initiating response-sequences of a certain behavior-family causes a disposition in some organism to respond under certain conditions by response-sequences of this behavior-family, then A is a sign.' (Morris 1946:10,17). Morris stresses that this characterization describes only the necessary conditions for the classification of something as a sign (Morris 1946:12).
This entire group of terms constitutes the subject matter of the intended science of signs (= semiotics) as viewed by Morris (Morris 1946:17). And based on this, he introduces certain additional terms for discussing this subject.
Already at this fundamental stage in the formation of the new science of signs, Morris has chosen 'behavioristics', as he calls it in line with von Neurath, as the point of view that he wishes to adopt in the case of semiotics. In the Foundations of 1938, he stresses that this decision is not necessary (cf. Morris 1971: 21) and also in his 'Signs, Language, and Behavior' of 1946, he explicitly discusses several methodological alternatives ('mentalistic', 'phenomenological' [Morris 1946:30 and Appendix]), but he considers a behavioristic approach more promising with regard to the intended scientific character of semiotics.
From today's point of view, it would no longer be necessary to oppose these different approaches to one another, but as this was the method used by Morris at that time, we will follow his lead for a moment.
Morris did not mention the problem of measurement explicitly. Thus the modes of measurement are - as in the case of Turing - restricted to normal perception; i.e., the subjective (= phenomenological) experience of an intersubjective situation restricted to observable stimuli and responses and the symbolic representation has been done in ordinary English (=L1) without any attempt at formalization.
Clearly, Morris did not limit himself to characterizing in basic terms the subject matter of his 'science of signs' but introduced a number of additional terms. Strictly speaking, these terms establish a structure which is intended to shed some theoretical light on 'chaotic reality'. In a 'real' theory, Morris would have 'transformed' his basic characterizations into a formal representation (as Turing did with his postulated computing person), which could then be formally expanded by means of additional terms if necessary. But he didn't. Thus we can put only some of these additional terms into ordinary English to get a rough impression of the structure that Morris considered important.
Morris used the term interpretant [INT] for all interpreter dispositions (= inner states) causing some response-sequence due to a 'sign = preparatory-stimulus'. And the goal-object of a response-sequence 'fulfilling' the sequence and in that sense completing the response-sequence Morris termed the denotatum of the sign causing this sequence. In this sense one can also say that a sign denotes something. Morris assumes further that the 'properties' of a denotatum which are connected to a certain interpretant can be 'formulated' as a set of conditions which must be 'fulfilled' to reach a denotatum. This set of conditions constitutes the significatum of a denotatum. A sign can trigger a significatum, and these conditions control a response-sequence that can lead to a denotatum, but do not necessarily do so: a denotatum is not necessary. In this sense, a sign signifies at least the conditions which are necessary for a denotatum but not sufficient (cf. Morris 1946:17ff). A formulated significatum is then to be understood as a formulation of conditions in terms of other signs (Morris 1946:20). A formulated significatum can be designative if it describes the significatum of an existing sign, and prescriptive otherwise. A sign-vehicle [SV] can be any particular physical event which is a sign (Morris 1946:20). A set of similar sign-vehicles with the same significata for a given interpreter is called a sign-family.
We will restrict our discussion of Morris to the terms introduced so far.
The fact that Morris did not translate these assumptions into a formal representation is a real drawback, because even these few terms contain a certain amount of ambiguity and vagueness.
Morris did not work out a computational model for his theory. At that time, this would have been nearly impossible for practical reasons. Besides, his theory was formally too weak to be used as a basis for such a model.
In order to take the next step and compare Morris with Turing, we will need at least an initial formalization of Morris's contribution. We will offer some ideas for such a formalization by presenting the first steps of such a process.
First, one must decide how to handle the 'dispositions' or 'inner states' (IS) of the interpreter I. From a radical behavioristic point of view, the interpreter has no inner states, but only stimuli and responses (cf. my discussion in Döben-Henisch 1998). Any assumptions about the system's possible internal states would be related to 'theoretical terms' within the theory which have no direct counterpart in reality. If one were to enhance behavioral psychology with physiology (including neurology) in the sense of neuropsychology, then one could identify internal states of the system with (neuro-)physiological states (whatever this would mean in detail). In the following, we shall assume that Morris would accept this latter approach. We shall label such an approach an S-N-R-theory or SNR-approach.
Within an SNR-approach, it is in principle possible to correlate an 'external' stimulus event S with a physiological ('internal') event S' as Morris intended: a stimulus S can exert an influence on some disposition D' of the interpreter I, or, conversely, a disposition D' of the interpreter can cause some external event R.
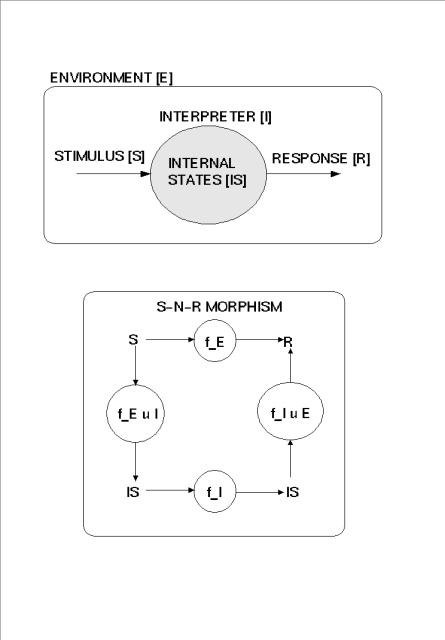
To work this out, one must assume that the interpreter is a structure with at least the following elements (cf. diagram 'SNR-MORPHISMs'):
I(x) iff x = <IS, <f_1, ..., f_n>, Ax>; i.e., an x is an Interpreter I if it has some internal states IS as objects (whatever these might be), some functions f_i operating on these internal states like f_i: pow(IS) ---> pow(IS), and some axioms stating certain general dynamic features. These functions we will call 'type I functions' and they are represented by the symbol 'f_I'.
By the same token, one must assume a structure for the whole environment E in which those interpreters may occur: E(x) iff x = <<I,S,R,O>, <p_1, ..., p_m>, Ax>. An environment E has as objects at least some interpreters I, something which can be identified as stimuli S or responses R, and, possibly, some additional objects O (without any further assumptions about the 'nature' of these different sets of objects). Furthermore, there must be different kinds of functions p_i, e.g.:
The overall constraint for all of these different functions is depicted in the diagram 'SNR-MORPHISMS'. This shows the basic equation f_E = f_E u I o f_I o f_I u E, i.e. the mapping f_E of environmental stimuli S into environmental responses R should yield the same result as the concatenation of f_E u I (mapping environmental stimuli S into internal states IS of an interpreter I), followed by f_I (mapping internal states IS of the interpreter I onto themselves), followed by f_I uE (mapping internal states IS of the interpreter I into environmental responses R).
Even these very rough assumptions make the functioning of the sign somewhat more precise. A sign as a preparatory stimulus S2 'stands for' some other stimulus S1 and this shall especially work in the absence of S1. This means that if S2 occurs, then the interpreter takes S2 'as if' S1 occurs. How can this work? We make the assumption that S2 can only work because S2 has some 'additional property' which encodes this aspect. We assume that the introduction of S2 for S1 occurs in a situation in which S1 and S2 occur 'at the same time'. This 'togetherness' yields some representation '(S1'', S2'')' in the system which can be 'reactivated' each time one of the triggering components S1' or S2' occurs again. If S2 occurs again and triggers the internal state S2', this will then trigger the component S2'', which yields the activation of S1'' which in turn yields the internal event S1'. Thus S2 -> S2' -> (S2'', S1'') -> S1' has the same effect as S1 -> S1', and vice versa. The encoding property is here assumed, then, to be a representational mechanism which can be reactivated constantly.
We shall stop at this preliminary formalization. It would be no problem to integrate phenomenological data and phenomenologically based functions into such a formalization as well, but we will not take this up at this point. Instead, we shall continue comparing Turing and Morris directly.
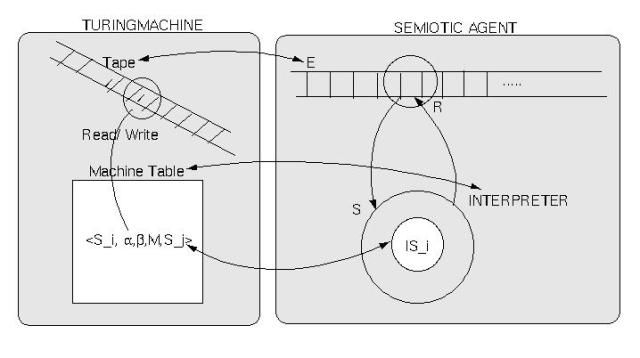
We shall compare Morris's interpreter with Turing's computing device, the Turing machine, in the light of our preliminary formalization by establishing informally a kind of mapping between the two (cf. diagram TURING-MORRIS).
It is clear what we have in the Turing machine: a tape with symbols [SYMB] which are arguments of the machine table [MT] of a Turing machine as well as values; i.e., we have MT: pow(SYMB) ---> pow(SYMB).
In the interpreter [I], we have stimuli [S] which are 'arguments' of the interpreter function f_E that yields responses [R] as values, i.e., f_E: pow(S) ---> pow(R). The interpreter function f_E can be 'refined' by replacing it by three other functions: f_EI: pow(S) ---> pow(IS_I), f_I: pow(IS_I) ---> pow(IS_I), and f_IE: pow(IS_I) ---> pow(R) so that
f_E = f_EI o f_I o f_IE.
(cf. the diagram 'SNRMORPHISM').
Now, because one can subsume stimuli S and responses R under the common class 'environmental events EV', and one can represent any kind of environmental event with appropriate symbols SYMB_ev, with SYMB_ev as a subset of SYMB, one can then establish a mapping of the kind
SYMB <--- SYMB_ev <----> EV <---- S u R.
What then remains is the task of relating the machine table MT to the interpreter function f_E. If the interpreter function f_E is taken in the 'direct mode' (the case of pure behaviorism), without the specializing functions f_E u I etc., we can establish directly a mapping
MT <---> f_E.
The argument for this mapping is straightforward: any version of f_E can be directly mapped into the possible machine table MT of a Turing machine, and vice versa. In the case of an interpreted theory, the set of 'interpreted interpreter functions' will very probably be a true subset of the set of possible functions.
If one replaces f_E by f_E = f_E u I o f_I o f_I u E, then we must establish a mapping of the kind
MT <---> f_E = f_E u I o f_I o f_I u E.
The compound function f_E u I o f_I o f_I u E operates on environmental states EV and on the internal states IS of the interpreter; i.e., the 'tape' of the Turing machine must be extended 'into' the interpreter.
The machine table MT of the Turing machine is 'open' to any interpretation of what 'kind of states' can be used to 'interpret' the general formula. The same holds true for Morris. He explicitly left open which concrete states should be subsumed under the concept of an internal state. The 'normal' attitude (at least today) would be to subsume 'physiological states'. But Morris pointed out (Morris 1946:30) that this might not be so; for him it was imaginable also to subsume 'mentalistic' states. And as has been pointed out above, it would not be difficult formally to integrate 'phenomenalistic' states. Thus, what all of these possible different interpretations have in common is to posit that states exist which can be identified as such and therefore can be symbolically represented. From this it follows that we can establish a mapping of the kind
SYMB <--- IS.
Because the tape - but not the initial argument and the computed value - of a Turing machine can be infinite, one must assume that the number of distinguishable internal states IS of the interpreter that are not functions is also 'finite'. This assumption makes sense: though it cannot be formally proved, it cannot be disproved either.
What remains is the mapping between MT and the compound interpreter function f_E u I o f_I o f_I u E. The only constraint on a possible interpretation of the states of a machine table MT is the postulate that the number of machine table states must be finite. In the case of the compound interpreter function f_E u I o f_I o f_I u E (which can be considered as a synthesis of many small partial functions), it also makes sense to assume that the number is finite. It is thus fairly straightforward to map any machine table into a function f_E u I o f_I o f_I u E and vice versa.
Thus we have reached the conclusion that an exhaustive mapping between Turing's Turing machine and Morris's interpreter is possible. This is a far-reaching result. It enables every semiotician working within Morris's semiotic concept to use the Turing machine to introduce all of the terms and functions needed to describe semiotic entities and processes. As a by-product of this direct relationship between semiotics 'à la Morris' and the Turing machine 'à la Turing', the semiotician has the additional advantage that any of his/her theoretical constructs can be used directly as a computer program on any computational machine. Thus 'semiotics' and 'computational semiotics' need no longer be separately interpreted, because what they both signify and designate is the same. Thus, one can (and should) claim that
semiotics = computational semiotics.
This equation makes of semiotics not only a potential player on the international science team but, even more, opens up the possibility that semiotics might be one of the scientific forerunners in the field of 'intelligent systems'. Whether semiotics can establish itself in the future as an original science based on the characterizing concept of the term 'sign' will strongly depend on new definitions of what a sign must be within such a formal framework. The short discussion above, occasioned by Morris's characterizations, shows that such a definition is far from trivial. It implies a complex mechanism of conditions and functions which must be worked out sufficiently clearly, an undertaking which has yet to be attempted.
W. BALZER: Empirische Theorien. Modelle, Strukturen, Beispiele. Braunschweig - Wiesbaden: Fr.Viehweg & Sohn 1982
W.BALZER/ C.U.MOULINES/ J.D.SNEED: An Architectonic for Science. The Structuralist Program, Dordrecht: Reidel 1987
N.BOURBAKI: Elements de Mathematique. Theorie des Ensembles, Paris: Hermann 1970
A.CHURCH: A set of postulates for the foundation of logic, In: Ann.Math. Ser.2, vol(33)1932, pp.346-366
A.CHURCH: A set of postulates for the foundation of logic, second paper. in: Ann.Math. Ser.2, vol(34)1934, pp.3839-844
A.CHURCH: The Richard paradox, In: Am.Math.Mo., vol(41)1934, pp.356-361
A.CHURCH: A proof from freedom of contradiction, In: Proc.Nat.Ac.Sci., vol(21)1935, pp.275-281
A.CHURCH: An unsolvable problem of elementary number theory, In: Amer.J.Math., vol.(58)1936, pp.345-363. Presented to the American Mathematical Society, April 19, 1935; abstract in B.Am.Math. S., vol(41), May 1935.
A.CHURCH: A note on the Entscheidungsproblem, In: Journal of Symbolic Logic, vol.1(1936a), pp:40-41, 356-361(received April 15, 1936). Correction ibid. (1936) 101-102; received August 13, 1936.
A.CHURCH: Reviews of Turing 1936-7 and Post 1936, In: Journal of Symbolic Logic, vol(2)1937, pp.42-43
A.CHURCH: A formulation of the simple theory of types, In: Journal of Symbolic Logic, vol(5)1940, pp:56-58
A.CHURCH/ S.C.KLEENE: Formal definitions in the theory of ordinal numbers, In: Fund. Math, vol(28)1937, pp:11-21
M.DAVIS (ed): The Undecidable. Basic Papers On Undecidable Propositions, Unsolvable Problems And Computable Functions, Hewlett (NY): Raven Press 1965
Gerd DÖBEN-HENISCH: Semiotic Machines - An Introduction, In: ERNEST W.HESS-LÜTTICH/ JÜRGEN E.MÜLLER (eds) Signs & Space - Zeichen & Raum. Tübingen: Gunter Narr Verlag, 1998, pp.313-327
B.DOTZLER/ F.KITTLER (eds): Alan Turing - Intelligence Service. Schriften. Berlin: Brinkmann & Bose Verlag 1987
Solomon FEFERMAN: Turing in the Land of O(z). In: R.HERKEN1988:113-147
Robin GANDY: The Confluence of Ideas in 1936. In: R.HERKEN 1988:55-111
K. GÖDEL: Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I. In: Mh.Math.Phys., vol.38(1931),pp:175-198
K. GÖDEL: Remarks before the princeton bicentennial conference on problems in mathematics 1946. In: DAVIS 1965:84-87
R.HERKEN (ed.): The Universal Turing Machine. A Half-Century Survey. , Hamburg - Berlin: Verlag Kammerer & Unverzagt 1988
D.HILBERT/ W.ACKERMANN: Grundzüge der theoretischen Logik. Berlin: Springer Verlag 1928
P.HINST: A Rigorous Set Theoretical Foundation of the Structuralist Approach. In: W. BALZER/ C.U.MOULINES (eds): Structuralist Theory of Science. Focal Issues, New Results. Berlin - New York: Walter de Gruyter Verlag 1996, 233-263.
A.HODGES: Alan Turing and the Turing Machine, In: R.HERKEN (ed)The Universal Turing Machine. A Half-Century Survey. Oxford - New York - Toronto: Oxford University Press 1988, pp. 3 - 15.
A.HODGES: Alan Turing, Enigma. Transl. by R.HERKEN/ E.LACK. Wien - New York:Springer-Verlag (engl.: 1983) 1994, 2nd ed.
Immanuel KANT: Kritik der reinen Vernunft, 1781/1787. New edited by R.SCHMIDT, Hamburg: Felix Meiner 1956
Stephen C. KLEENE: General recursive functions of natural numbers, In: Math.Annal., vol(112)1936, pp.727-742. Presented by title to theAmerican Mathematical Society Sept 1935. Abstract in B.Am.Math. S., July 1935.
Stephen C. KLEENE: lambda-definability and recursiveness, In: Duke Math.J., vol(2)1936a, pp.340-353. Abstract in B.Am.Math. S., July 1935.
Stephen C. KLEENE: Introduction to Metamathematics. Amsterdam: North Holland Publ. Co. 1952
Stephen C. KLEENE/ J.B.ROSSER: The inconsistency of certain formal logics, In: Ann.Math., Ser.2, vol(36)1935, pp.630-636, Abstract in B.Am.Math.Soc., January 1935
William KNEALE/Martha KNEALE: The Development of Logic. Oxford: Clarendon Press 1962, repr. 1986
G.LUDWIG: Die Grundstrukturen einer physikalischen Theorie, Berlin - Heidelberg - New York: Springer 1978
G.LUDWIG: Einführung in die Grundlagen der Theoretischen Physik, Braunschweig: Viehweg 1978b (2nd. ed.)
Charles W. MORRIS: Symbolik und Realität,1925. German translation of the unpublished dissertation of Morris by Achim ESCHBACH. Frankfurt: Suhrkamp Verlag, first published 1981
Charles W. MORRIS: Die Einheit der Wissenschaft, 1936. German translation of an unpublished lecture by Achim ESCHBACH, In: MORRIS 1981, Suhrkamp Verlag, Frankfurt, pp.323-341
Charles W. MORRIS: Logical Positivism, Pragmatism, and Scientific Empiricism. Paris: Hermann et Cie. 1937
Charles W. MORRIS: Foundations of the Theory of Signs, 1938. Chicago: University of Chicago Press (repr. In: MORRIS 1971)
Charles W. MORRIS: Signs, Language and Behavior. New York: Prentice-Hall Inc. 1946
Charles W. MORRIS: Philosophie als symbolische Synthesis von Überzeugungen, 1947. German transl. of an article in: BRYSON, Jerome et al (eds.) "Approaches to Group Understanding", New York. The german transl. is published in: Charles W. MORRIS [1981]
Charles W. MORRIS: The Open Self. New York: Prentice-Hall Inc.1948
Charles W. MORRIS: Die Wissenschaft vom Menschen und die Einheitswissenschaft. German transl. of an article in: Proceedings of the American Academy of Arts and Sciences, vol.80(1951) pp.37-44. The german transl. is published in: Charles W. MORRIS [1981]
Charles W. MORRIS: Towards a Unified Theory of Human Behavior. New York: Prentice Hall Inc.1956
Charles W. MORRIS: Signification and Significance. A Study of the Relations of Signsc and Values. Cambridge (MA): MIT Press 1964
Charles W. MORRIS: Writings on the General Theory of Signs. The Hague - Paris: Mouton Publ. 1971, pp.148-170
Winfried NÖTH: Handbuch der Semiotik. Stuttgart: J.B.Metzlerische Verlagsbuchhandlung 1985
Roland, POSNER: Research in Pragmatics after Morris, In: Dedalus, vol(1)1991, pp.115-156
Emil L. POST: Introduction to a general theory of elementary propositions, In: Am.J.Math. , vol(43)1921, pp.163-185 (repr. In van HEIJENOORT 1967).
Emil L. POST: Finite combinatory processes-Formulation 1., In: Journal of Symb.Logic, vol(1)1936, pp.103-105; received Oct 7, 1936. Presented to theAmerican Mathematical Society Jan 1937. Abstract in B.Am.Math. S., Nov 1936.
Emil L. POST: Formal reductions of the general combinatorial decision problem, In: Am. J.Math., vol(65)1943, pp.197-215
Emil L. POST: Recursively enumerable sets of positive integers and their decision problems, In: B.Am.Math.Soc., vol(50)1944, pp.258-316 (repr. In DAVIS 1965)
Emil L. POST: Recursive Unsolvability of a Problem of Thue, In: JSL vol(12)1947, pp.1-11, includes some critical remarks to TURINGs 'On computable numbers...'. (repr. In DAVIS 1965:293-303)
Emil L. POST: Absolutely unsolvable problems and relatively undecidable propositions: Account of an anticipation (submitted for publication in 1941). Printed in DAVIS 1965, pp.340-433
S. SUPPE (ed): The Structure of Scientific Theories, Urbana - Chicago - London: University of Illinois Press 1977 (2nd ed.1979)
A.M.TURING: On Computable Numbers with an Application to the Entscheidungsproblem, In: Proc. London Math. Soc., Ser.2, vol.42(1936), pp.230-265; received May 25, 1936; Appendix added August 28; read November 12, 1936; corr. Ibid. vol.43(1937), pp.544-546. Turing's paper appeared in Part 2 of vol.42 which was issued in December 1936 (Reprint in M.DAVIS 1965, pp.116-151; corr. ibid. pp.151-154).
A.M.TURING: Computability and lambda.definability, In: J.Symb.Log., vol(2)1937, pp.153-163
A.M.TURING: Systems of Logic based on ordinals, In: Proc.London Math.Soc, Ser.2, vol(45)1939, pp.161-128
A.M.TURING: Proposal for development in the mathematics division of an Automatic Computing Engine (ACE), 1945. Report E882, Executive Committee NPL. Reissued in 1972 with a forword by D.W.DAVIES as NPL reprot., In. Comp.Sci., vol(57) (repr. In TURING 1986).
A.M.TURING: Computing machinery and intelligence, In: Mind, vol. 59(1950), pp. 433 - 460. German Translation in: B.DOTZLER u. F. KITTLER (eds.), [1987], pp.147 - 280
A.M.TURING: A.M.Turing's ACE Report of 1946 and Other Papers, ed. by CARPENTER, R.E./ DORAN, R.W., Cambridge (MA): MIT Press and Los Angeles:Tomash Publ. 1986
A.M.TURING: Intelligente Maschinen, In: Intelligent Service - Schriften, Hrsg.v. B.DOTZLER u. F. KITTLER 1987: pp. 81 - 113. (Engl.: Intelligent Machinery ( 1948)).
J. van HEIJENOORT: From Frege to Gödel: A Source Book in Mathematical Logic 1879-1931. Cambridge (MA) : Harvard University Press 1967