|
|
I-THINF WS 0203 - Vorlesung mit Übung
|
An der Wurzel der Informatik stand Anfang des 20.Jh. die Frage der (Meta-)Mathematiker nach einem effizienten Verfahren. In Gestalt der Turingmaschine wurde 1937 ein Konzept in die community eingeführt, das die grösste Akzeptanz fand und sich bislang als die stärkste Version eines berechenbaren Verfahrens erwiesen hat (Churche These). Im Zusammenhang der Diskussion um die Fähigkeiten der universellen Turingmaschine konnte gezeigt werden, dass universelle Turingmaschinen -verglichen mit der Struktur biologischer Nervensysteme- prinzipiell veränderbar und damit prinzipiell lernfähig sind. Am Beispiel des verhaltensbasierten psychologischen Intelligenzbegriffes wurde deutlich gemacht, dass man methodisch korrekt auch von 'intelligenten Maschinen' sprechen kann, sofern man sich auf das Verhalten dieser Maschinen bezieht und dieses in Beziehung setzt zu den üblichen psychologischen Tests. Am Beispiel der minimalen strukturellen Anforderung für ein System, das sprachlich kommunizieren können soll (siehe Schaubild)
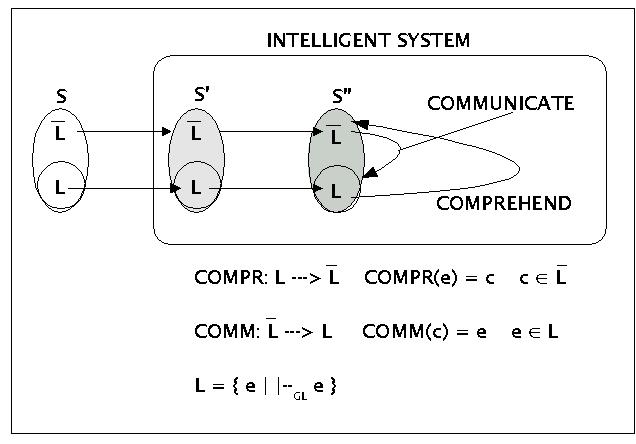
Basics of Language Communications
wurde ferner erklärt, dass es bis heute keine wirklich funktionierenden Modelle für sprachlernende Systeme gibt. Hier existiert also eine aktuelle Herausforderung an die Informatik.Traditionellerweise beschränkt sich die Informatik auf die Ausdrucksseite von Sprachen, und hier auch nur auf die sogenannten formalen Sprachen, die geeignet sind, Automaten zu steuern. Dabei wird immer angenommen, dass die jeweiligen Sprachen bzw. Grammatiken fest sind, d.h. mit keinerlei Veränderungsprozessen (Adaptation, Lernen) verknüpft sind. Ein typisches Schema für die bisherige Verwendung formaler Sprachen in der Informatik ist das folgende:
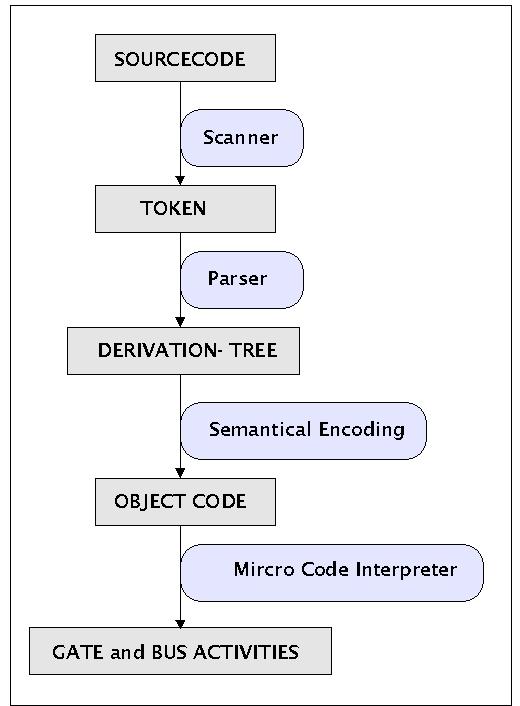
Different Levels of Languages
Es gibt einen Text, den sogenannten Quelltext (engl. 'source code'), der Ausdrücke einer vereinbarten Sprache L2 enthält. Mittels eines Scanners wird dieser Text so analysiert, dass alle die Schlüsselwörter, die in der Sprache L2 wichtig sind, als sogenannte Tokens identifiziert werden. Auf der Basis dieser Tokens versucht dann ein Parser festzustellen, ob die Token in der richtigen/ korrekten Weise angeordnet sind. Ist dies der Fall, dann lassen sich mit den Tokens sogenannte Ableitungsbäume (engl. 'derivaten trees' oder 'parse trees') erzeugen.
An dieser Stelle könnte man die Betrachtung abbrechen, da jetzt entschieden wäre, ob der eingegebene Quelltext tatsächlich korrekte Ausdrücke der Sprache L2 enthält. Im Normalfall interessieren aber nicht die korrekten Ausdrücke als solche, sondern man will die erkannten Ausdrücke dazu benutzen, um ganz bestimmte Aktionen/ Operationen in einer Maschine auszulösen. D.h. man muss diesen Ausdrücken aus L2 nun bestimmte Maschinenzustände zuordnen. Dies geschieht in mindestens zwei Schritten. Im ersten Schritt werden den korrekten Ausdrücken der Sprache L2 elementare Ausdrücke L1 einer virtuellen Maschine zugeordnet (z.B. Maschinensprache einer bestimmten CPU), und im zweiten Schritt werden diese Ausdrücke L1 dann über den Mikrokode einer CPU in Ereignisse L0 im Bereich der Gatter und der Busse übersetzt. Dies ist Thema der Vorlesung Rechnerarchitektur. In diesem Rahmen stellen die Audrücke von L1 dann die Bedeutung der Ausdrücke von L2 dar und die Ereignisse von L0 die Bedeutung der Ausdrücke von L1.
Formale Sprachen repräsentieren Systeme von Ausdrücken, die aus einfachen Grundelementen (Zeichen, Symbolen, Buchstaben) gebildet werden. Um eine formale Sprache L zu definieren, muss man im wesentlichen festlegen, welche Kombinationen von Grundelementen erlaubt sein sollen. Eine Möglichkeit, um solch eine Beschreibung realisieren zu können, besteht in der Angabe einer formalen Grammatik G für eine sprache L, also G(L). Formale Grammatiken G(L) kann man dann dazu benutzen, um korrekte Ausdrücke der Sprache L zu erzeugen/ generieren/ synthetisieren, oder aber um von einem vorgelegten Ausdruck E sagen zu können, ob er zur Menge L(G) der durch die Grammatik G definierten korrekten Ausdrücke L gehört; dies nennt man dann den Ausdruck E parsen/ analysieren/ erkennen.
Es folgen jetzt eine Reihe von Begriffen, die benötigt werden, um über formale Sprachen sprechen zu können.
Alphabet [A]: das Alphabet bildet die endliche Menge der Grundelemente einer Sprache L.
Sei A solch ein Alphabet. Wenn x in A dann heisst x gewöhnlich ein Buchstabe ('letter') oder Symbol
('symbol') oder zeichen ('sign'). Vielfach wird statt dem Buchstaben 'A' zur Abkürzung für Alphabet auch dr Buchstabe
'V' (engl. 'vocabulary') benutzt.
ALPHABET(A) gdw A ist eine endliche Menge.
Wort über A: Die Aneinanderfügung von Zeichen aus A ergibt eine Zeichenkette ('string') über
A bzw. ein Wort ('word') über A. Sei A1= {a,b}, dann wären 'aaa', 'abb', 'a', 'b' usf. solche Worte über A.
Mengentheoretisch kann man ein Wort über A auffassen als eine endliche
Folge auf der Menge A (FSON(w,A)], durch die ein Anfangsabschnitt der natürlichen Zahlen Nat auf die Menge des Alphabetes A
abgebildet wird. Ausführlich geshrieben: 'aaa' := <a1,a2,a3, >, 'abb' :=
<a1,b2,b3, >. Sofern dies nicht zu unnötigen Mehrdeutigkeiten führt, wird im folgenden
immer die Kurzschreibweise für Worte benutzt, ohne die Indizes.
WORD(w,A) gdw FSON(w,A), z.B. WORD(<a1,b2,b3, >,{a,b}) oder kurz: WORD('abb',{a,b})
Leeres Wort [§]: Es gibt genau ein Wort der Länge 0, das ist das leere Wort und es wird hier geschrieben '§' (in der Literatur meist kleines Epsilon oder kleines Lambda).
Länge eines Wortes w |w|: Die Länge eines Wortes w über dem Alphabet A wird mit |w| bezeichnet.
Menge aller Wörter über A [A*] Alle Kombinationen von Buchstaben aus A sind Wörter über A. Auch das leere Wort, sodass A* leer sein kann. (während das Alphabet A nach Voraussetzung endlich ist gilt dies für A* nicht) .
Menge der nichtleeren Wörter über A [A+]: A+ = A* \ {§}
Sprache, formale Sprache: Jede Teilmenge von A* wird als Sprache oder Formale Sprache bezeichnet.
LANGUAGE(L) gdw (E:A)( ALPHABET(A) & L C A* ).
Halbgruppe mit neutralem Element (Monoid) <A*, o >: Mittels der Menge A* und der Operation Konkatenation 'o' lässt sich jetzt eine Struktur <A*, o > als Halbgruppe mit neutralem Element (Monoid) definieren, die folgende Eigenschaften haben soll:
Für alle x,y in A* soll gelten:
x o y = xy in A* (Abgeschlossenheit)
(x o y ) o z = x o ( y o z ) = xyz (Assoziativität)
§ o x = x o § = x (Neutrales Element)
Damit kann man vereinbaren: wenn w, u1,u2, v Worte über einem Alphabet A sind, dann gilt:
wn = ww ...w (n-mal) (eine n-fache Konkatenation)
speziell gelte w0 = §.
|w| := Länge eines Wortes; Anzahl der Zeichen in dem Wort w, wobei jedes Zeichen sooft gezählt wird, wie es vorkommt; mit den zusätzlichen Eigenschaften:
|§| = 0
|u1,u2,| = |u1|, + |u2,|
|wn| = n * |w|
v ist ein Teilwort von w wenn w = u1vu2. Wenn u1 = § dann ist v ein Präfix, ist u2 = § dann ist v ein Suffix. Jedes Wort w ist trivialerweise Teilwort, Präfix und Suffix von sich selbst; ebenso gilt dies für das leere Wort §.
Seien A,B Teilmengen von ALPH* mit ALPH als einem Alphabet, dann sind A und B Sprachen. folgende Begriffe werden benötigt:
A u B = { x | x in A oder x in B }
A cut B = { x | x in A und x in B }
c(A) (auch Querstrich über A) = ALPH* - A
AB = { xy | x in A und y in B }
A0 = {§}
A1 = A
An+1 = AAn
AiAj=(Ai)+j
A* = U (n > 0) An
A+ = U (n > 1) An
Beispiele für Alphabete:
A = {|} unärer Strichcode zur elementaren Darstellung natürlicher Zahlen
A = {0,1} zur Darstellung von Binärzahlen
A = {0,1,...9} zur Darstellung von ganzen Dezimalzahlen
A = {a,b,...,z,A,B, ...,Z} zur Darstellung von Wörtern aus Gross- und Kleinbuchstaben
A = ASCII (übernommen von Stefan Lenz).
Der ASCII-Code ist eine standardisierte Zeichen-Definition für den Datenaustausch zwischen Informatik-Systemen. ASCII bedeutet American Standard Code for Information Interchange. Es ist sozusagen «der kleinste gemeinsame Nenner» aller Informatik-Systeme. ASCII wurde 1968 mit der Intention oder Absicht entwickelt, Datenübertragungen zwischen divergierenden Hardware- und Softwaresystemen zu standardisieren.
Alle Zeichen im Bereich von 0 bis 127 gehören zum Standard ASCII-Zeichensatz. Dieser Standardzeichensatz von 0 bis 127 ist in der IT-Welt stark normiert. Die Zeichen werden aus einem 1 Byte dargestellt, das heisst es sind maximal 256 Zeichen möglich, auf PC-Systemen kommt der erweiterte ASCII-Zeichensatz (0 bis 255) zum Einsatz.
Die ASCII-Zeichen 0 bis 32 werden als Steuerzeichen bzw. Formatierungszeichen für Ein- und Ausgabegeräte verwendet.
Jeder Satz von Zeichen, der den ASCII-Werten zwischen dezimal 128 und 255 (hexadezimal 80 bis FF) zugeordnet ist. Die Zuordnung spezifischer Zeichen zu den erweiterten ASCII-Codes variieren zwischen Computern und zwischen Programmen, Schriften oder grafischen Zeichensätzen. Erweitertes ASCII erhöht auch die möglichen Funktionen, da sich mit den 128 zusätzlichen Zeichen z. B. Akzentbuchstaben, Umlaute, grafische Zeichen und spezielle Symbole darstellen lassen.
A = EBCDIC (übernommen von ASCII-EBDIC).
Der Enhanced Binary Coded Decimal Interchange Code (gesprochen: eb-sih-dik) ist die von IBM für Mainframes benutzte proprietäre Zeichenkodierung. Es ist ein 8-bits-Code, so dass 256 Steuerzeichen, Ziffern, Buchstaben und Sonderzeichen binär dargestellt werden können. Erstmals eingesetzt wurde er auf Lochkarten (engl.: punched card) in den 60er Jahren des vorigen Jahrhunderts. Für die Internationalisierung wurden mehrere verschiedene Code-Tabellen herausgegeben, nur in der so genannten International Reference Version (IRV) sind alle Zeichen des ISO/IEC 646, der die Zeichen des 7-bits--ASCII standardisiert, enthalten. Der ursprüngliche BCD-Code beschränkte sich durch die Verwendung von 4 bits auf die Darstellung des Zahlenbereiches von 0 bis 15.
Abzählbar ist eine Menge M, wenn man ihre Elemente entsprechend einer Ordnung wie im Beispiel der natürlichen Zahlen Nat anordnen kann: 0-tes Element, erstes Element, ... Man kann also vereinbaren:
ABZÄHLBAR(m) gdw (E:f)( f: Nat ---> m & SURJEKTIV(f) )
ÜBERABZÄHLBAR(m) gdw ¬ABZÄHLBAR(m)
Alle endlichen Mengen sind mit dieser Definition trivialerweise abzählbar. Wie verhält es sich mit unendlichen Mengen?
In der Mengenlehre unterscheidet man grundsätzlich zwischen abzählbar unendlichen und überabzählbar unendlichen Mengen.
Kardinalität: Sei x eine Menge, dann wird durch |x| die Kardinalität der Menge (x die Anzahl der Elemente) repräsentiert.
Zwei Mengen x1 und x2 haben die gleiche Kardinalität, wenn es eine 1-zu-1-Abbildung zwischen x1 und x2 gibt.
Seien x, y endliche Mengen und sei x C y; dann gilt |x| <= |y|.
Abzählbar unendliche Menge: Als Prototyp für eine abzählbar unendliche Menge ('countably infinite') dient die Menge der natürlichen Zahlen Nat. Mengen mit der gleichen Kardinalität wie die natürlichen Zahlen Nat gelten ebenfalls als abzählbar unendlich. Es gibt viele Mengen, die gleichmächtig sind mit der Menge Nat, z.B.: die Menge der geraden oder die Menge der ungeraden Zahlen, die Menge der Zweierpotenzen, die Menge der rationalen Zahlen usw.
Den Aufweis, dass die Menge der rationalen Zahlen abzählbar unendlich ist, führte als erster Georg Cantor mit dem sogenannten ersten Cantorschen Diagonalverfahren.
Eine Menge M heisst (höchstens) abzählbar ('countable') falls sie endlich ist oder abzählbar unendlich.
Überabzählbar unendlich: Schon CANTOR entdeckte, dass es im Bereich der unendlichen Mengen Unterschiede bzgl. der Abzählbarkeit gibt. So konnte CANTOR in einem Brief vom 7.Dezember 1873 einem Freund einen Beweis mitteilen, dass die Menge der reellen Zahlen Rel nicht-abzählbar ist, da sie mächtiger ist als die Menge der natürlichen Zahlen; die Menge der rellen Zahlen Rel wird als überabzählbar unendlich bezeichnet. Für den Beweis der Nichtabzählbarkeit der rellen Zahlen genügt es, einen Abschnitt der reellen Zahlen zwischen zwei beliebigen Zahlen [0,1] zu betrachten und zu verabreden, dass alle reellen Zahlen in diesem Intervall als unendliche Dezimalbrüche darzustellen sind. Indirekt angenommen, es gäbe zu diesen Zahlen eine Abzählung, dann könnte man diese Zahlen so anordnen, dass man jeder dieser Zahlen eindeutig eine natürliche Zahl zuordnen könnte. Welche Anordnung man aber auch immer wählen mag, aufgrund der Anordnung generiert man eine relle Zahl, die nicht in der Abzählung vorkommt. Damit ist die Nichtabzählbarkeit bewiesen.
Unter anderem kann man dann auch beweisen, dass jede Teilmenge von Rel von gleicher Kardinalität ist wie Rel insgesamt.
Satz: Die Menge aller Wörter A* über einem Alphabet A ist abzählbar. Der Beweis ordnet alle Wörter einmal der Länge nach an, und innerhalb der Länge lexikographisch. Dann kann man jedem element eine natürliche Zahl zuordnen.
Satz: Jede Teilmenge M' einer abzählbaren Menge M ist abzählbar. Für den Fall, dass M endlich ist, ist der Nachweis trivial. Ist M nicht endlich, dann gibt es zu M eine surjektive Abbildung f: Nat ---> N. Für die abzählbarkeit von M' benötigt man eine Funktion f': Nat ---> M'. Da M' ene Teilmenge von M ist und M = rn(f) gilt M' C rn(f); dann ist f' = f |\ M'.
Satz: Da für jede Sprache L zu einem Alphabet A gilt, L C A*, folgt aus den beiden vorausgehenden Sätzen, dass jede Sprache L über dem Alphabet A abzählbar ist.
Aufzählbar (rekursive aufzählbar, semientscheidbar): eine Menge M ist aufzählbar, falls es eine surjektive Funktion f: Nat ---> M gibt, und f ist eine turingberechenbare Funktion.
Aufzählung von M: ist die Menge M aufzählbar und ist f die turingberechenbare Funktion zu M, dann ist die Folge <f(0), f(1), ... > eine Aufzählung von M
Satz: Jede endliche Menge ist aufzählbar. Sei M eine endliche Menge. Eine Turingmaschine m bildet eine Folge von Zahlen '|', '||', ... solange, bis alle Elemente der Menge M abgearbeitet sind.
Satz: Die Menge aller Wörter A* über einem Alphabet A ist aufzählbar. Eine Turingmaschine m bildet eine Folge von Worten aus A nach der Länge und lexikographisch geordnet.
Satz: Jede aufzählbare Menge ist auch abzählbar
Bilden sie ein Team von 5 Mitgliedern
Erstellung Sie gemeinsam einen Text mit Namen und Matr.Nr. der AutorenInnen. Abgabe einer Kopie des Textes an den Dozenten vor Beginn der Übung.
Präsentation der Lösung als Team vor der gesamten Gruppe. Präsentationszeit (abhängig von der Gesamtzahl der Teams) 3-5 Min.
Was unterscheidet biologische Systeme, die mit natürlicher Sprache kommunizieren von den Systemen der Informatik, die Sprache verarbeiten?
Welches sind die Stufen der Sprachverarbeitung in einem Computer, wenn man vom Quellcode einer Programmiersprache oberhalb der Assemblersprachen beginnt?
Was ist der Unterschied zwischen abzählbar unendlich und überabzählbar unendlich?
Was ist der Unterschied zwischen abzählbar und aufzählbar?
Entwerfen sie einen Algorithmus, der die Menge der natürlichen Zahlen in Binärdarstellung aufzählt.