1. Einführung

In der ersten Sitzung wurde, ausgehend von den Grundlagenfragen der modernen Mathematik im Ausgang des 19.Jh und zu Beginn des 20.Jh, verdeutlicht, dass dem Begriff des effektiven Verfahrens eine zentrale Bedeutung zukommt, will man 'klar' entscheiden, ob eine formale Theorie T widerspruchsfrei und vollständig ist.

Zu Beginn gab es drei Formalismen, die als Präzisierungen des Begriffs 'effektives Verfahren' akzeptiert wurden: die allgemein rekursiven Funktionen von Herbrand und Gödel, der Lambda-Kalkül von Church und die Turingmaschine von Alan Matthew Turing.

Im weiteren Verlauf konnte nicht nur die Äquivalenz dieser drei Präzisierungen nachgewiessen werden, sondern es wurden im Laufe der Zeit eine Reihe weiterer Formalismen gefunden, für die ebenfalls eine Äquivalenz nachgewiessen werden konnte.

Die bekanntesten Formalismen lassen sich auf drei Grundtypen zurückführen: auf den Begriff der Funktion, auf den Begriff des Automaten sowie auf den Begriff der Grammatik. Alle diese drei Konzepte kann man dazu benutzen, um Sprachen zu charakterisieren, entweder dadurch, dass man sagt, welche sprachlichen Ausdrücke akzeptiert/ erkannt werden oder welche generiert/ erzeugt werden können (für einen ersten Überblick zu Automaten, Sprachen und Grammatiken siehe hier

Während die Logik und Metamathematik an diesen Präzisierungen des Begriffs des effektiven Verfahrens vorwiegend bis ausschliesslich nur interessiert waren, um damit grundlagentheoretische Sachverhalte entscheiden zu können, gewannen diese neuen Präzisierungen der Berechenbarkeit in dem sich darauf aufbauenden Gebiet der (theoretischen) Informatik ein neues Eigenleben. Man entdeckte, dass sich mit diesen neuen Konzepten nicht nur neuartige Maschinen -nämlich elektronische Rechenmaschinen, Computer, Roboter usw. (siehe die Vorlesung Rechnerarchitektur)- bauen liessen, sondern man konnte damit auch eine Reihe von praktischen Aufgaben auf neue Weise lösen.

Ein Hauptziel dieser Lehrveranstaltung ist es, die wichtigsten Automaten, die dazu äquivalenten Grammatiken sowie die damit behandelbaren Sprachen kennenzulernen. Zusätzlich sollen Fragen der Komplexität behandelt werden. Ansatzweise sollen auch Brücken geschlagen werden zu biologischen Strukturen wie Nervenzellen und Nervensystemen, die die prominentesten Repräsentanten für biologische Strukturen der Informationsverarbeitung darstellen.

Um dieses Ziel zu erreichen wird in einem ersten Schritt heute das Konzept der Turingmaschine an einem praktischen Beispiel und in einer Formalisierung vorgestellt. Daran anknüpfend wird erläutert, in welchem Sinne eine Turingmaschine sowohl eine Funktion wie auch eine Grammtik simulieren kann.

START

2. Informelle Darstellung einer Turingmaschine

Wir beginnen die detaillierteren Überlegungen mit der Turingmaschine, dem mächtigsten Automaten, der bislang als Präzisierung des Begriffs eines effektiven Verfahrens identifiziert werden konnte.

Dieser geht zurück auf Alan Matthew Turing (1912 - 1954). Wir geben hier zunächst eine informelle Beschreibung und ein Beispiel (wer mehr Beispiele und mehr Informationsmaterial zum Thema Turingmaschine sucht, kann im Internet schnell fündig werden; das WWW ist dicht bevölkert mit allerlei Arten von Turingmaschinen, oft sogar online verfügbar; eine einfache TM in der Spache C findet sich hier).

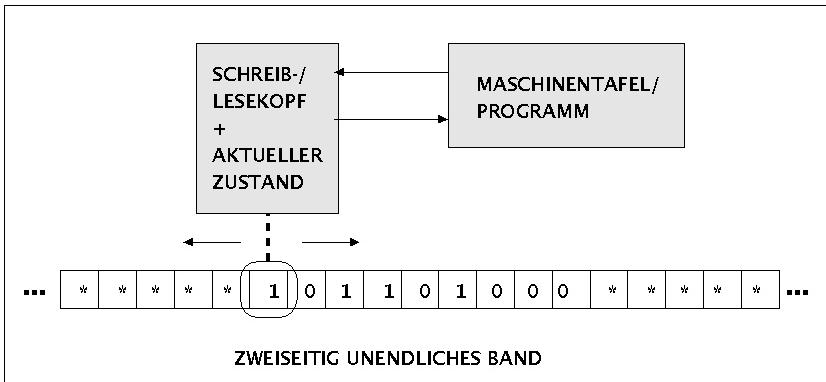
Deterministische 1-Band Turingmaschine

Wir wählen hier die Form der deterministischen Turingmaschine (DTM) mit einem Band.. Wie später gezeigt wird, sind andere Formen von Turingmaschinen (1/2-Band, mehrere Bänder, universelle Turingmaschine, nichtdeterministische Turingmaschine usw. nicht stärker als eine DTM).

Intuitiv besteht eine Turingmaschine aus einem nach beiden Seiten offenen Band ('tape'), das gleichmässig in rechteckige Felder ('squares') unterteilt ist. Zu Beginn einer Rechnung ist das Band leer bis auf eine endliche Menge von Symbolen I aus einem endlichen Alphabet A, die nacheinander auf das Band geschrieben sind, pro Feld ein Symbol. Alle anderen Felder enthalten das leere Zeichen '§', das nicht zum Alphabet A gehört: das Bandalphabet G = A + {§} (In der Literatur gibt es eine Vielzahl von Konventionen zur Bezeichnung des leeren Feldes {'b', 'B', 'kleines Epsilon', 'leeres Quadrat, 'Unterstrich mit Winkeln nach oben', '*', lambda usw.}. Das Alphabet A ist nicht leer. Zu Beginn der Rechnung steht der Schreib-Lese-Kopf genau über dem ersten Feld der Inschrift I. Die Turingmaschine befindet sich im Start-Zustand q₀. Die Menge aller Zustände Q ist endlich. Neben dem Startzustand q₀ enthält sie noch eine endliche Menge von Endzuständen ('final states') F = {q_f.1, ...,q_f.k } mit k > 1 und, falls man will, auch noch Fehlerzustände (error states') E = {q_e.1, ...,q_e.s } mit s > 0. . Die Aktionen einer DTM sind in der Maschinentafel, dem 'Programm' der Turingmaschine, festgelegt. Eine Maschinentafel besteht aus einer endlichen nichtleeren Menge von Übergangsregeln D, wobei eine einzelne Übergangsregel d_i die Form hat:

Eine andere häufige Schreibweise ist auch:

Eine einzelne Übergangsregel ist wie folgt zu lesen:

1. q_i: wenn der aktuelle Zustand q_i ist

2. v_j: und das Zeichen, das aktuell vom Schreib-Lesekopf gelesen wird, v_j ist,

3. q'_i: dann soll der nächste Zustand q'_i sein,

4. v'_j: und als Zeichen soll auf das aktuelle Feld das Zeichen v'_j geschreieben werden

5. h_i: und der Schreib-Lesekopf soll in Richtung h_i bewegt werden.

v_j, v'_j sind aus G = A u {§} und
h_i ist aus {'L', 'R', 'S'}; es bedeutet 'L' := auf dem Band ein Feld nach 'links', 'R' := auf dem Band ein Feld nach 'rechts', 'S' := Stop, keine Bewegung mehr. Ein Zustand q_i als erstes Element einer Übergangsregel, bei dem als letztes Element ein Stop-Symbol 'S' steht, heisst ein zeichenbedingter Endzustand. Davon zu unterscheiden sind jene zustandsbedingte Endzustände, die die Maschine stoppen unabhängig davon, welches Symbol gelesen wird und welche Richtung im letzten Element einer Übergangsregel angegeben ist.

Beginnend mit dem Startzustand q₀ auf dem ersten Zeichen einer Inschrift I wird eine DTM also einzelne Aktionen anhand der Menge der Übergangsregeln in der Maschinentafel ausführen. Grundsätzlich sind nun drei Fälle denkbar:

1. Eine DTM mit Argument I gerät in eine Endlosschleife

2. Eine DTM mit Argument I gerät nicht in eine Endlosschleife und hat nach n-vielen Aktionen gestoppt

3. Eine DTM mit Argument I gerät nicht in eine Endlosschleife aber hat nach n-vielen Aktionen noch nicht gestoppt

Tritt Fall (2) ein, dann soll die Konvention gelten, dass die DTM die ursprüngliche Eingabe I gelöscht hat und der Schreib-Lesekopf am Ende wieder auf dem ersten Zeichen des Ergebnisses steht; das Ergebnis kann leer sein.

START

3. Eine Turingmaschine, die subtrahiert

Bevor wir die Turingmaschine ganz formalisieren und wir weitere Eigenschaften betrachten, sei hier eine konkrete Turingmaschine für eine bestimmtes Problem gegeben (siehe auch die hervorragende Seite zur Turingmaschine der Universität Wuppertal).

Das nachstehende Programm vollführt eine Subtraktion mit ganzen Zahlen x,y: x-y. Dabei werden folgende Fälle berücksichtigt:

1. Keine Eingabe:= das Band ist leer, entspricht einer 0

2. '_b_':= nur ein Minuszeichen, entspricht 0-0, ergibt 0

3. 'a ...ab' := x-0, ergibt x

4. 'ba ...a' := 0-x, ergibt 0

5. 'a...aba...a' := x-y mit x=y, ergibt 0

6. 'a...aba...a' := x-y mit x >y, ergibt z >0

7. 'a...aba...a' := x-y mit x <y, ergibt 0

#---------------------------------------
# TM-Programm 'subtract'
# AUTOR: G.DOEBEN-HENISCH Oct-4 2002
# BEFEHLSFORMAT: <Akt.Zustand, Lesezeichen, Folge-Zustand, Schreibzeichen, Bewegung>
#---------------------------------------

#---------------------------------------
# TESTFAELLE
#
# FALL (0)
# 0
# Leeres Band
#
# FALL (i)
# 0-0 = 0
# '_b_'
#
# FALL (ii)
# x-0 = x
# 'a ... ab'
#
# FALL (iii)
# 0-x = 0
# 'ba...a'
#
# FALL (iv)
# x-y = 0 (mit x=y)
#
# FALL (v)
# a-y = z (mit x>y, z > 0)
# a_1 ... a_kba_1 ... a_L (L < K)
#
# FALL (vi)
# x-y = 0 (mit y >x)
# a_1 ... a_kba_1 ... a_L (L <= K)
#
#
#---------------------------------------

# ALPHABET = {a,b}
# BANDALPHABET = ALPHABET + Leerzeichen
# BEGINN PROGRAMM
# ERSTE ZEILE

ab 0123456789ABEF ab 0 EF

# FALL (0)

0 E S
0a1aR
0b7 R

# FALL (ii) - (vi)\(iii)

1a1aR
1b2bR
1 F S

# FALL  (ii) - (vi))\(iii)

2a4aR
2 3 L
2bFbS

# FALL (ii)

3a3aL
3b3 L
3 E L

# FALL (iv) - (vi)

4a4aR
4bFbS
4 5 L

# FALL  (iv) - (vi)

5a6 L
5bFbS
5 F S

# FALL  (iv) - (vi)

6a6aL
6b8bL
6 F R

# FALL (i) UND (iii)

7a7 R
7 E S
7bFbS

# FALL  (iv) - (vi)

8 9 R
8aAaL
8bFbS

# FALL (vi)

9a9 R
9b9 R
9 E S


# FALL (iv) oder (v)

AaAaL
AbFbS
A B R

# FALL (iv) oder (v)

Ba1 R
BbFbS
B F S


# (E) Ende

EaEaS
EbEbS
E E S

# (F) Fehler

FaFaS
FbFbS
F F S

 

Unter Benutzung des einfachen TM-Simulators von Andreas Jung (vormals Universität Rostock) ergibt sich folgende Abarbeitung bei der Eingabe des Argumentes 'aaaba' (:= 3-1):

Wort ueber {ab } eingeben: aaaba
================================================================|
aaaba
0
========================== ENTER, Anzahl Schritte oder '.' =====>
aaaba
 1
========================== ENTER, Anzahl Schritte oder '.' =====>
aaaba
  1
========================== ENTER, Anzahl Schritte oder '.' =====>
aaaba
   1
========================== ENTER, Anzahl Schritte oder '.' =====>
aaaba
    2
========================== ENTER, Anzahl Schritte oder '.' =====>
aaaba
     4
========================== ENTER, Anzahl Schritte oder '.' =====>
aaaba
    5
========================== ENTER, Anzahl Schritte oder '.' =====>
aaab
   6
========================== ENTER, Anzahl Schritte oder '.' =====>
aaab
  8
========================== ENTER, Anzahl Schritte oder '.' =====>
aaab
 A
========================== ENTER, Anzahl Schritte oder '.' =====>
aaab
A
========================== ENTER, Anzahl Schritte oder '.' =====>
 aaab
A
========================== ENTER, Anzahl Schritte oder '.' =====>
 aaab
 B
========================== ENTER, Anzahl Schritte oder '.' =====>
  aab
  1
========================== ENTER, Anzahl Schritte oder '.' =====>
  aab
   1
========================== ENTER, Anzahl Schritte oder '.' =====>
  aab
    1
========================== ENTER, Anzahl Schritte oder '.' =====>
  aab
     2
========================== ENTER, Anzahl Schritte oder '.' =====>
  aab
    3
========================== ENTER, Anzahl Schritte oder '.' =====>
  aa
   3
========================== ENTER, Anzahl Schritte oder '.' =====>
  aa
  3
========================== ENTER, Anzahl Schritte oder '.' =====>
  aa
 3
========================== ENTER, Anzahl Schritte oder '.' =====>
  aa
E
========================== ENTER, Anzahl Schritte oder '.' =====>
  aa
E
Turingmaschine akzeptiert.
================================================================|
 

Die Simulation liefert das korekte Ergebnis 'aa' := 2 und stoppt im Endzustand 'E' (Zustände werden in diesem Simulator hexadezimal kodiert; der Simulator 'verkraftet' auch nicht mehr als 16 Zustände...).

Damit der TM-Simulator von Andreas Jung die Programmdatei verarbeiten kann, muss man die Kommentarzeilen entfernen. Dies kann man mit dem Shell-Befehl 'egrep' und der Option '-v' erreichen; man leitet die Ausgabe des Befehls dann in eine eigene Datei:

 gerd@goedel:~/WEB-MATERIAL/fh/I-THINF/TH-THINF/VL2> egrep -v '#' subtract.tm >subtr.tm

Dann kann man das Programm mit Namen 'turing.linux' im Verzeichnis 'http://www.fbmnd.fh-frankfurt.de/~doeben/I-THINF/TH-THINF/VL2' wie folgt aufrufen:

gerd@goedel:~/WEB-MATERIAL/fh/I-THINF/TH-THINF/VL2> ./turing.linux subtr.tm
Turingmaschinen-Simulator - (C) 1996 by DL9AAI
==============================================

Eingabealphabet: {ab}
Zustandsmenge  : {0123456789ABEF}
Bandalphabet   : {ab }
Startzustand   : 0
Endzustaende   : {EF}
Produktion    0: 0  |-> E S
Produktion    1: 0a |-> 1aR
Produktion    2: 0b |-> 7 R
Produktion    3: 1a |-> 1aR
Produktion    4: 1b |-> 2bR
Produktion    5: 1  |-> F S
Produktion    6: 2a |-> 4aR
Produktion    7: 2  |-> 3 L
Produktion    8: 2b |-> FbS
Produktion    9: 3a |-> 3aL
Produktion   10: 3b |-> 3 L
Produktion   11: 3  |-> E L
Produktion   12: 4a |-> 4aR
Produktion   13: 4b |-> FbS
Produktion   14: 4  |-> 5 L
Produktion   15: 5a |-> 6 L
Produktion   16: 5b |-> FbS
Produktion   17: 5  |-> F S
Produktion   18: 6a |-> 6aL
Produktion   19: 6b |-> 8bL
Produktion   20: 6  |-> F R
Produktion   21: 7a |-> 7 R
Produktion   22: 7  |-> E S
Produktion   23: 7b |-> FbS
Produktion   24: 8  |-> 9 R
Produktion   25: 8a |-> AaL
Produktion   26: 8b |-> FbS
Produktion   27: 9a |-> 9 R
Produktion   28: 9b |-> 9 R
Produktion   29: 9  |-> E S
Produktion   30: Aa |-> AaL
Produktion   31: Ab |-> FbS
Produktion   32: A  |-> B R
Produktion   33: Ba |-> 1 R
Produktion   34: Bb |-> FbS
Produktion   35: B  |-> F S
Produktion   36: Ea |-> EaS
Produktion   37: Eb |-> EbS
Produktion   38: E  |-> E S
Produktion   39: Fa |-> FaS
Produktion   40: Fb |-> FbS
Produktion   41: F  |-> F S

(1) TM auf ein Wort ansetzen
(2) TM auf eine Konfiguration ansetzen
(3) L(T) aufzaehlen
(4) TM auf alle Woerter ansetzen
(0) Programm beenden

Ihre Wahl: 1

START

4. Das Programm einer Turingmaschine als Zustands-Graph

Turingmaschinenprogramme lassen sich auf verschiedene Weisen hinschreiben. Oben liegt eine Schreibweise vor, die sich nahe an der formalen Definition von Übergängen (Produktionen, 'productions') orientiert.

Eine andere Variante stellt eine Übergangstabelle ('transition table') dar. Ein Teil einer solchen Übergangstabelle ist nachstehend angedeutet. In einer Übergangstabelle stehen z.B. in der linken Spalte die Indizes aller Zustände und in der oberen Zeile stehen die möglichen Zeichenvorkommnisse auf dem Band. An den Kreuzungspunkten von Zustandsnummern und Inputzeichen stehen dann die auszuführenden Aktionen, z.B.:

Für die Darstellung einer Turingmaschinentabelle in einem Computer ist dies sicher sehr praktisch; für die Verdeutlichung der Zusammenhänge aus der Sicht eines menschlichen Benutzers eher nicht. Für diese Zwecke gibt es aber auch die Möglichkeit, die Zustände zu visualisieren, als Knoten in einem Netzwerk. Siehe dazu die nachfolgende Tabelle als Übersetzung des vorausgehenden Subtraktionsprogrammes in ein Netzwerk von Zuständen:

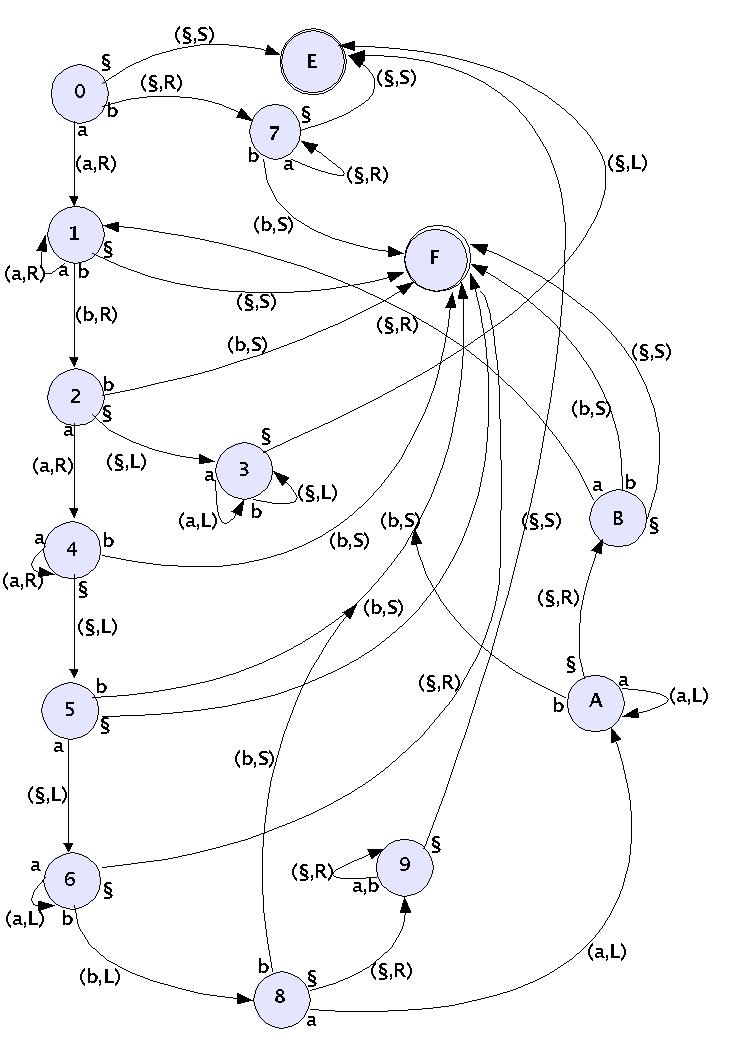
TM für Subtraktion ganzer Zahlen

Ein Zustand wird durch einen Kreis mit der Zustandsnummer repräsentiert. Für jedes Zeichen, das ein Zustand von einem Band lesen kann, gibt es einen eigenen Ausgang, der als Pfeil dargestellt wird. Am Usprung des Pfeils steht der Name des Bandzeichens, das in diesem Zustand gelesen werden kann (im Beispiel sind dies die Zeichen 'a', 'b' und '§'). Etwa in der Mitte des Pfeiles steht dann jenes Zeichen, das geschrieben werden soll, und die Richtung, in die sich der Kopf bewegen soll. An der Spitze des Pfeiles befindet sich dann der Zustand, in den bei Aktivierung dieses Pfeils übergegangen werden soll. Wie man sieht, kann ein Zustand auch in sich selbst übergehen (Für die genaue Definition eines Zustandes siehe weiter unten).

Anmerkung: bei der Darstellung einer Turingmaschine als Zustandsgraphen kann sich eine Assoziation mit den Nervenzellen eines biologischen Nervensystems aufdrängen. Versucht man, eine etsprechende Abbildung zwischen den Zuständen einer Turingmaschine und den Nervenzellen eines Nervensystems herzustellen, dann fallen auf den ersten Blick sofort Unterschiede auf:

1. In einer Turingmaschine kann immer nur ein Zustand aktiv sein; in einem Nervensystem sind aber alle Nervenzellen gleichzeitig aktiv, d.h. an jeder Nervenzelle können simultan Ereignisse auftreten ('Zeichen gelesen werden') und auf diese wird simultan eine Antwort generiert.

2. Ferner ist zu beachten, dass jede Nervenzelle mehr als einen Eingang haben kann (bis 70.000 und mehr!). Diese Eingänge können partiell auch 'beschrieben' werden. Von daher muss man für jede Nervenzelle ein Band fordern, was bedeuten würde, dass man entweder das ganze Gehirn in soviel Bänder zerlegt denken muss, wie es Nervenzellen gibt oder aber, dass es k-viele Bänder gibt, in deren Abschnitten simultan mehr als eine Nervenzelle zugreifen kann.

3. Schliesslich ist noch festzuhalten, dass lebende Nervensysteme sich selbst, d.h. ihre Struktur, bis zu einem gewissen Grade ereignisgetrieben 'umbauen' können; sie können auf diese Weise in bestimmtem Umfang ihr Verhalten ändern.

Im weiteren Verlauf der vorlesung soll auch überlegt werden, ob ein biologisches Nervensystem dadurch qualitativ mehr kann als eine Turingmaschine oder ob diese Unterschiede nur marginal sind.

START

5. Formalisierung einer Turingmaschine

Damit kann man nun folgende formalisierte Darstellung einer deterministischen Turingmaschine (DTM) geben:

mit

1. Q:= endliche nichtleere Menge von Zuständen

2. E := Menge der Endzustände; E C Q & E != 0

3. A:= endliches Alphabet; |A| > 0

4. G = A u {§}; das endliche Bandalphabet

5. § := das leere Zeichen

6. q₀ := der Anfangszustand; q₀ in Q

7. M = {'L', 'R', 'S'}; endliche Menge von Richtungsaktionen ('links', 'rechts', 'stop')

8. P ist das Programm der Turingmaschine t und es gilt P_t: Q_t-E_t x G_t ---> Q_t x G_t x M_t

9. PRules_t C P_t; Die Produktionsregeln PRules sind eine Teilmenge des Turingmaschinen Programms P_t

10. Production_t(p) gdw p in PRules_t; p ist eine Produktion (Production), wenn p Element der Produktionsregeln; statt von 'Produktion' spricht man auch oft von 'Übergangsregel'

11. p in PRules_t ==> p = <s_i,a,s_j,b,m > mit actual_state_t (p) = s_i

12. States_t = {s | s C PRules_t & (A:x,x')(x,x' in s ==> actual_state_t(x) = actual_state_t(x') }

13. k ist eine Konfiguration einer Turingmaschine m: CONFIGURATION(k,m) gdw m ist eine deterministische Turingmaschine & k ist eine Zeichenkette 'aqb' mit a,b aus G_m* und q aus Q_m. Auf dem Band befindet sich die Inschrift I = ab, eingerahmt von Blanks, und der Schreiblesekopf im Zustand q steht auf dem ersten Zeichen von b. Folgende Fälle sind hier zu unterscheiden:

    1. q ist der Startzustand q₀ und a ist leer; dies nennen wir eine Startkonfiguration ('START_CONFIGURATION') und b die Eingabe der Turingmaschine;

    
    
    2. q ist ein Endzustand und a ist wiederum leer (zum Ende steht immer nur das Ergebnis auf dem Band), also q_endb; dies nennen wir auch eine Endkonfiguration ('END_CONFIGURATION') und b das Ergebnis;

    
    
    3. q ist weder Start- noch Endzustand.

    
    

14. Die Menge der Konfigurationen ('configurations') einer Turingmaschine m: configurations(m) = { k | CONFIGURATION(k,m) }




15. Direkte Nachfolgekonfiguration einer Turingmaschine m: eine 'direkte Nachfolgekonfiguration' von aqb ist die Zeichenkette a'q'b', wenn a'q'b' aus aqb durch Anwendung einer Übergangsregel d_i entstanden ist. Man schreibt:
    
    

    aqb |--_m a'q'b'
    
    

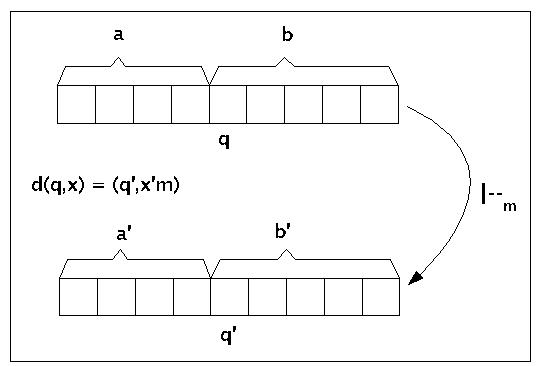
    Direkte Ableitung einer TM-Konfiguration

    
    

    Die neue Konfiguration unterscheidet sich von der vorhergehenden Konfiguration maximal durch eine neue Position des Schreib-Lesekopfes und möglicherweise durch eine Veränderung der Inschrift.




16. P ist ein Protokoll ('protocol') mit der Länge n von der Turingmaschine m für die Eingabe x : PROTOCOL(P,m,x,n) gdw P ist ein Tupel der Länge n & rn(P) C configurations(m) & (A:i)( i in dm(P) ==> k_i |-- k_i+1 mit i < n )




17. k' ist die Nachfolgekonfiguration von k bei einer Turingmaschine m oder k' ist ableitbar von k mit einer Turingmaschine m: ABL(k',k,m) gdw (E:P,n)( PROTOCOL(P,m,k,n) & END_CONFIGURATION(k',m) & k' = P_n. Statt ABL(k',k,m) schreibt man auch:
    
    

    k |*--_m k'




18. n ist die Länge ('length') einer Ableitung einer Turingmaschine m für die Eingabe k: k |*--_m k' ==> lenth(k,k',m) = n gdw (E:P) PROTOCOL(P,m,k,n)




19. Der INPUT x einer Turingmaschine m: INPUT(x,m) gdw TM(m) & '§q₀x' ist eine Startkonfiguration von m




20. Rechenzeit: die Rechenzeit einer DTM ist die Zahl der Zustandsübergänge, bis die TM, angesetzt auf die Eingabe k mit dem Ergebnis k' stoppt. Da jeder endlichen Berechnung eine Ableitung korrespondiert, kann man auch sagen, die Rechenzeit entspricht der Länge der Ableitung von k' aus k unter m.




21. Die Eingabe x wird von einer Turingmaschine m akzeptiert ('accepted'): ACCEPT(x,m) gdw DTM(m) & §q₀x |*-- §q'y & q' in E und 'y' steht für 'YES'




22. Die Eingabe x wird von einer Turingmaschine m nicht akzeptiert ('rejected'): REJECT(x,m) gdw DTM(m) & §q₀x |*-- §q'n & q' in E'n' steht für 'NOT'




23. Die von einer Turingmaschine m erkannte Sprache L: L(m) = { x | TM(m) & ACCEPT(x,m) }




24. Simulation: Ein Automat M' simuliert einen Automat M gdw für jedes Argument w mit M(w) = w' gilt M'(w) = w'. Damit ist vereinbar, dass der Platz- und/oder Zeitbedarf von M' grösser oder kleiner ist als von M (so gilt z.B., dass eine Registermaschine (s.u.) sich von einer der Varianten der Turingmaschine im Zeitverbrauch maximal um einen polynomialen Faktorunterscheidet).

Im Rahmen der Komplexitätstheorie (s.u.) wird die deterministische Turingmaschine (DTM) benutzt, um die Komplexitätsklasse P zu definieren. Zur Definition der Komplexitätsklasse NP benötigt man eine andere Variante der Turingmaschine, nämlich eine nichtdeterministische Turingmaschine (NDTM). Nichtdeterministische Turingmachinen zeichnen sich dadurch aus, dass sie in jedem Zustand nicht nur genau eine Fortsetzung kennen, sondern u.U. mehr als eine. Man kann dies entweder so realisieren, dass man die Übergangsfunktion entsprechend abändert oder aber, und das ist die Variante die hier benutzt werden wird, man ergänzt eine DTM um ein 'Schätzmodul' ('guessing module').

START

6. Übungsaufgabe

START