|
|
RECHNERARCHITEKTUR WS 0203 - Vorlesung mit Übung
|
In der heutigen Vorlesung soll der Überblick über die sogenannten Programmierbaren Logischen Schaltungen (PLDs, engl. 'Programmable Logical Devices') ausgeweitet werden. Diese Schaltungen spielen in der Anwendung eine immer grössere Rolle. Speziell werden dann sequentielle Automaten betrachtet, die man mit solchen PLDs realisieren kann. Zum Verständnis der PLDs sei nochmals hingewiessen auf das Konzept der aussagenlogischen Normalformen, die als theoretische Konzepte dem Aufbau der PLDs zugrunde liegen.
Die Verwendung der Begriffe im Umkreis programmierbarer logischer Bausteine (PLDs) ist in der Literatur nicht einheitlich. Für die folgende Darstellung beziehe ich mich in der Terminologie auf [NÜHRMANN 1998:3732ff], da dieser sich sehr eng an die Terminologie anlehnt, die in der Industrie üblich ist.
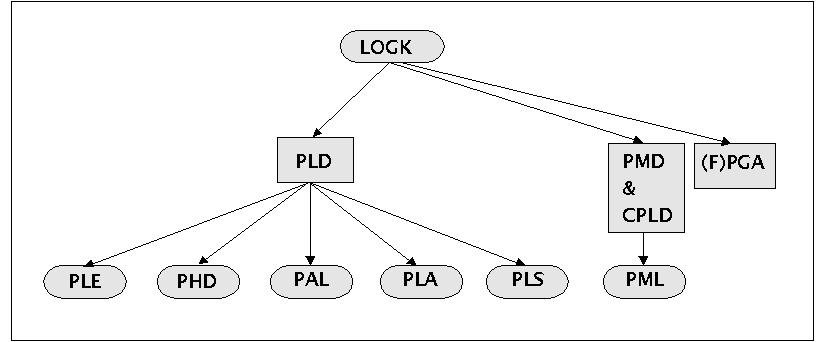
PLD Stammbaum nach NÜHRMANN
LOGIK: Obergebgriff für Logikbausteine
PLD: Programmierbare Logikbausteine (engl. 'Programmable Logic Devices')
PMD & CPLD: Programmierbarer Macro-Baustein (engl. 'Programmable Macro Device'). Sammelbegriff für neue PLDs mit hoher Packungsdichte, welche sich nicht den PGAs noch den Clustered PLDs zuordnen lassen.
(F)PGA:Programmierbare Gate Arrays (engl. 'Field Programmable Gate Arrays'). Anwenderprogrammierbares Gate Array mit einer sehr grossen Anzahl von frei verbindbaren Basiselementen. Neben den 'flüchtigen' reprogrammierbaren Versionen (auf RAM-Basis) gibt es auch nichtflüchtige OTP-Versionen mit 'Antifuse'-Verbindungstechnologie (z.B. amorphes Silizium)
PLE: Programmierbare Logikelemente (engl. 'Programmable Logic Elements'). Bezeichnung für Speicherbausteine, z.B. PROMS.
PHD: Herstellerbezeichnung für programmierbare Adressdekoder (engl. 'Programmable High-Speed Decoder')
PAL: Programmierbare (AND)-Array Logik (engl. 'Programmable (AND)-Array Logic'. *PAL* ist auch ein Warenzeichen. PLD mit programierbaren UND-Gatter nd festen ODER-Gattern.
PLA: Programmierbare Logik Arrays (engl. 'Programmable Logic Arrays'). Diese Bausteine umfassen frei programmierbare UND und ODER-Gatter mit wählbarer Ausgangspolarität.
PLS: Programmierbare Logik Sequencer (engl. 'Programmable Logic Sequencer') oder Zustandsmaschine (engl. 'state machine'). Universell programmierbare Zustandsmaschinen-Bauelemente mit Array Aufbau gemaess PLA.
PML Programmierbare Macro Logic (engl. 'Programmable Macro Logic'). Herstellerbezeichnung für eine PMD-Architektur hoher funktionsdichte. Statt AND- und OR-Gattern werden rückgekoppelte NAND-Gattern mit bis zu 256 Eingängen verwendet.
GAL Generische (AND-)Array Logik (engl. 'Generic (AND-)Array Logic').*GAL* ist auch ein Warenzeichen. Universelle PALs mit pogrammierbaren ausgangsfunktionen (kombinatorisch oder sequenteiell) durch *OMC*. OMC := Output Macro Cell: Konfigurierbare Output-Macro-Celle zur Nachbildung aller typischen PAL-Ausgangsstrukturen duch Programmierung einer Konfigurationszelle
Die prinzipielle Architektur von PLDs wird im folgenden Schaubild gezeigt.
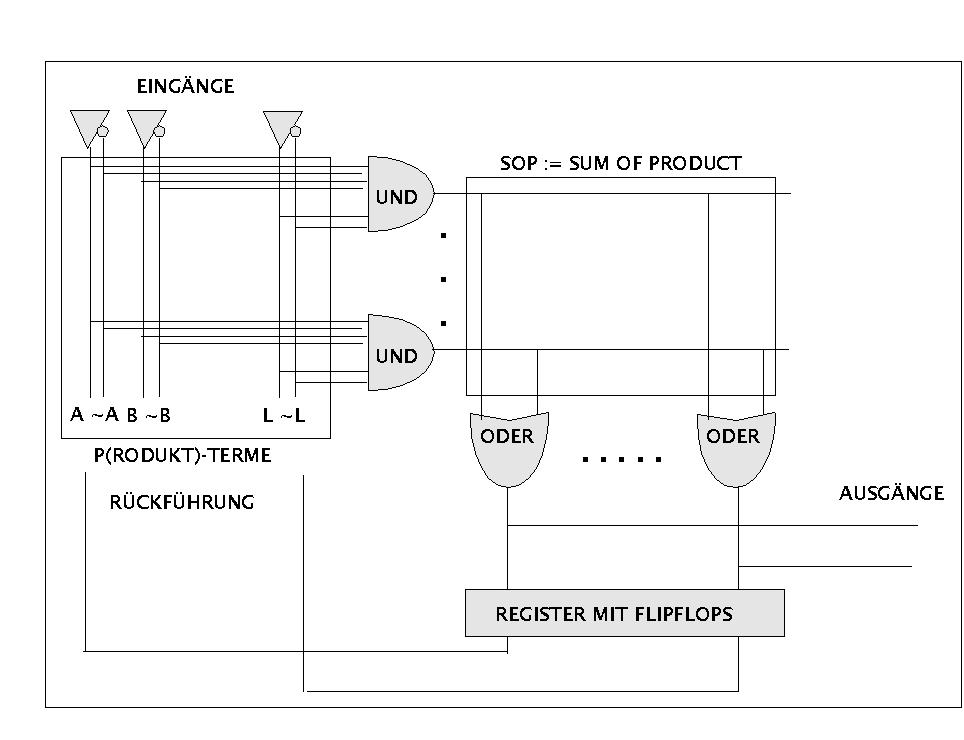
Zur allgemeinen Struktur von PLDs
Eingänge samt ihren Negationen werden über eine Matrix einer Serie von UND-Gattern so zugeführt, dass jedes UND-Gatter mit jedem Eingang verbunden werden kann. Die konkrete Verbindung ist entweder fest vorgegeben oder frei programmierbar (alle, ausser PLE). Die Gesamtheit der UND-Gattern formen mit ihren Eingängen die sogenannten Produkt-Terme (s.u.). Die Ausgänge der UND-Gatter werden wiederum über eine Matrix einer Serie von ODER-Gattern zugeführt. Auch hier kann jedes ODER-Gatter prinzipiell mit jedem Ausgang verknüpft werden. Je nach Baustein sind diese Verbindungen fest verdrahtet oder sie sind frei programmierbar (PLE, PLA, PLS, evtl PLM). Die Gesamtheit der ODER-Gatter mit ihren Eingängen formen die Summe der Produkte (engl. 'SOP := Sum of Products'). Einige Bausteine haben zusätzliche Flipflops als Haltezustände an den Ausgängen -die dann ein Register bilden-, die über eine Rückkoppelung wieder als Eingänge in das System zurückgeführt werden. Fest verdrahtete Flipflops finden sich bei PAL und PML, frei programmierbare bei PLS (evtl. PML). Zusätzlich können weitere Macros auftreten (nicht im Bild), und zwar bei PAL, PLS und PML.
Aus der Sicht boolscher Funktionen stellt die UND-ODER-Architektur von PLDs eine maximal allgemeine Struktur dar. Dies liegt darin begründet, dass sich mit dieser Struktur (nur durch die konkrete Anzahl beschränkte) beliebige disjunktive Normalformen realisieren lassen, also mit drei Eingängen A, B und C z.B. (A & ~B & C) + (~A & ~B & ~C). Wie aus der Theorie der boolschen Funktionen bekannt, kann man jeden boolschen Ausdruck in eine äquivalente (konjunktive oder) disjunktive Normalform umformen. Dies bedeutet in diesem Kontext, dass man mit dieser UND-ODER-Gatter Struktur jede boolsche Funktion realisieren kann. Bei einer grossen Zahl von UND-Gattern macht es dann Sinn, 'Untergruppen' von UND-Gattern zu bilden, die dann unterschiedliche ODER-Gatter ansteuern. Man hat dann mehrere boolsche Funktionen simultan auf dem Chip.
Jene Bausteine (speziell PLS), die zusätzlich über frei programmierbare Flipflops verfügen, bieten die Möglichkeit, mittels der Haltezustände der Flipflops 'Zustände' zu repräsentieren und durch Rückführung auf die Eingänge der Schaltung 'zu erinnern'. Dies ermöglicht die technische Realisierung sogenannter sequentieller Automaten (oder auch endliche automaten, engl. 'finite state automaton').
Ein sequentieller Automat ist ein endlicher Automat (engl. 'finite state automaton (FSA)' oder 'finite state machine (FSM)'), der sich von einer Turingmaschine nur dadurch unterscheidet, dass er keine Möglichkeit hat, das Verhalten des Lese-Schreib-Kopfes selbständig zu beeinflussen. Im Prinzip kann man sich das Verhalten eines endlichen Automaten so vorstellen (siehe Bild), dass das Band in zwei Hälften geteilt ist: irgendwo gibt es ein leeres Feld '§'; links davon steht eine Inschrift, die den Input für den Automaten bildet und der Lesekopf steht auf den ersten k-vielen Feldern des Inputs; rechts von dem leeren Feld steht der Schreibkopf, der zugleich m-viele Felder abdecken kann. Der Lesekopf kann sich bei jeder Aktion nur k-viele Felder nach links bewegen und der Schreibkopf m-viele Felder nach rechts. Alles, was der Schreibkopf nach rechts hin schreibt, ist der Output des Automaten.
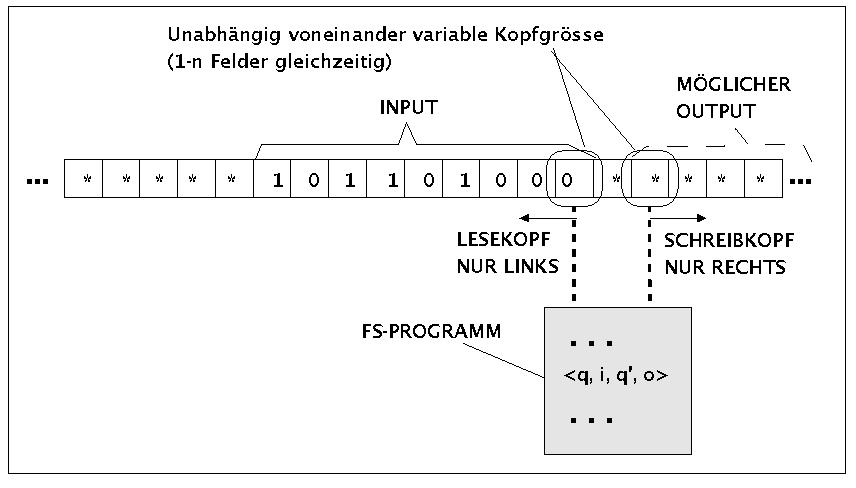
Die 'Idee' eines sequentiellen Automaten = endlicher Automat
Das Programm eines endlichen Autmaten ähnelt dem einer Turingmaschine, nur fehlen hier die Richtungsangaben für den Lese-Schreib-Kopf. In der folgenden formalisierung kann man die Ähnlichkeit mit der turingmaschine sofort erkennen. Sämtliche begriffe sind übertragbar; man muss nur einige Besonderheiten des endlichen Automaten übertragen, die sich aus der fehlenden 'Eigenbewegung' ergeben.
FSM(t) gdw t = < < Q, E, I, O, {§}, {q0 } >, < P > >
mit
Q:= endliche nichtleere Menge von Zuständen
E := Menge der Endzustände; E C Q & E != 0
I:= endliches Eingabe-Alphabet; |I| > 0
O:= endliches Ausgabe-Alphabet; kann leer sein
B = I u {§}; das endliche Bandalphabet
§ := das leere Zeichen
q0 := der Anfangszustand; q0 in Q
P ist das Programm des endlichen Automaten t und es gilt
P: Q -E x G --->
Q x O
Speziell beim endlichen Automaten interessiert auch die folgende Aufspaltung von P in zwei Teilfunktionen F und
G:
P = F u G
mit
F: Q -E x G ---> Q
G: Q -E x G ---> O
Die Funktion F berechnet zu einem aktuellen Zustand q und zu einem aktuellen Input i den Nachfolgezustand q'. Entsprechend die
Funktion G den neuen Output o.
PRules C P; Die Produktionsregeln PRules sind eine Teilmenge des Programms P
Production(p) gdw p in PRules; p ist eine Produktion (Production), wenn p Element der Produktionsregeln ist; statt von 'Produktion' spricht man auch oft von 'Übergangsregel'
p in PRules ==> p = <si,a,sj,b> mit actual_state(p) = si
States = {s | s C PRules & (A:x,x')(x,x' in s ==> actual_state(x) = actual_state(x') }
k ist eine Konfiguration einer endlichen Maschine m: CONFIGURATION(k,m) gdw m ist ein endlicher Automat & k ist eine Zeichenkette 'aqb§g' mit a,b aus I* und g aus O* und q aus Q. 'aqb' repräsentiert den Input mit der aktuellen Position des Lesekopfes und Zustandes q unter dem ersten Zeichen rechts von b sowie dem aktuellen Output g mit dem Schreibkopf rechts vom letzten Zeichen von g. Folgende Fälle sind hier zu unterscheiden:
q ist der Startzustand q0 und die Konfiguration hat die Form 'aq§' mit dem Lesekopf unter dem ersten Zeichen rechts von a und dem Schreibkopf rechts vom ersten Blank rechts von a.Dies nennen wir eine Startkonfiguration ('START_CONFIGURATION') und a die Eingabe der Turingmaschine;
q ist ein Endzustand und und die Konfiguration hat die Form 'qab§g' mit dem Lesekopf links von dem ersten Zeichen von a und dem Schreibkopf rechts vom letzten Zeichen von g, wobei g leer sein kann. Dies nennen wir auch eine Endkonfiguration ('END_CONFIGURATION') und g das Ergebnis;
q ist weder Start- noch Endzustand.
Die Menge der Konfigurationen ('configurations') eines endlichen Automaten m: configurations(m) = { k | CONFIGURATION(k,m) }
Direkte
Nachfolgekonfiguration eines endlichen Automaten m: eine 'direkte Nachfolgekonfiguration' von aqb§g ist die
Zeichenkette a'q'b'§g', wenn a'q'b'§g' aus aqb§g durch Anwendung einer Übergangsregel di
entstanden ist. Man schreibt:
Die neue Konfiguration unterscheidet sich von der vorhergehenden Konfiguration maximal durch eine neue Position des Lesekopfes und möglicherweise durch eine Veränderung des des Schreibkopfes mit Veränderung des Outputs
P ist ein Protokoll ('protocol') mit der Länge n von dem endlichen Automaten m für die Eingabe x : PROTOCOL(P,m,x,n) gdw P ist ein Tupel der Länge n & rn(P) C configurations(m) & (A:i)( i in dm(P) ==> ki |-- ki+1 mit i < n )
k' ist die Nachfolgekonfiguration von k bei einem endlichen Automaten m oder k' ist ableitbar von k mit einem
endlichen Automaten m: ABL(k',k,m) gdw (E:P,n)( PROTOCOL(P,m,k,n) & END_CONFIGURATION(k',m) & k' = Pn. Statt
ABL(k',k,m) schreibt man auch:
n ist die Länge ('length') einer Ableitung eines endlichen Automaten m für die Eingabe k: k |*--m k' ==> lenth(k,k',m) = n gdw (E:P) PROTOCOL(P,m,k,n)
Der INPUT x eines endlichen Automaten m: INPUT(x,m) gdw FSM(m) & '§aq0§' ist eine Startkonfiguration von m
Rechenzeit: die Rechenzeit eines endlichen automaten FSA ist die Zahl der Zustandsübergänge, bis der FSA, angesetzt auf die Eingabe k mit dem Ergebnis k' stoppt. Da jeder endlichen Berechnung eine Ableitung korrespondiert, kann man auch sagen, die Rechenzeit entspricht der Länge der Ableitung von k' aus k unter m.
Die Eingabe x wird von einem endlichen Automaten m akzeptiert ('accepted'): ACCEPT(x,m) gdw FSM(m) & §xq0§ |*-- §qex§g & qe in E und 'g' steht für 'YES'
Die Eingabe x wird von einem endlichen Automaten m nicht akzeptiert ('rejected'): REJECT(x,m) gdw FSM(m) & §xq0§ |*-- §qex§g & qe in E und 'g' steht für 'NO'
Die von einem endlichen Automaten m erkannte Sprache L: L(m) = { x | FSM(m) & ACCEPT(x,m) }
Analog zum Fall des Turingmaschinenprogramms kann man auch das Programm eines endlichen Automaten dirtekt in ein Zustandsdiagramm übertragen. An den Übergangspfeilen zwischen zwei Zustandskreisen fehlt gegenüber dem Fall der Turingmaschine nur die Angabe der Richtung der Lese-Schreib-Köpfe, da diese festliegt.
Nach so viel Theorie hier ein Beispiel. Das folgende Beispiel eines sequentiellen Automaten, der als Volladdierer arbeitet, ist dem Buch [MÄRTIN et al 2002:105ff] entnommen. Das nachfolgende Bild zeigt einen Zustandsgraphen des sequentiellen Automaten für den einsatz als Volladdierer ohne Endzustände.
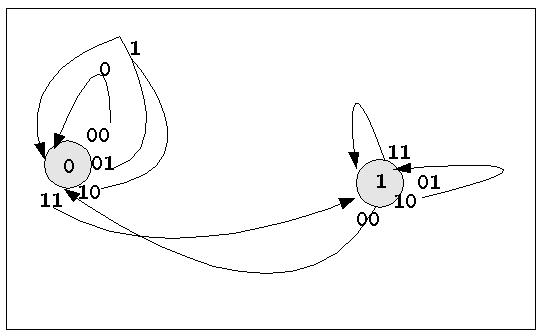
Zustandsgraph des Sequentiellen Automaten für Volladdition
Angenommen wird eine Situation, in der dem Automat zwei Binärzahlen übergeben werden, und er addiert diese Binärzahlen bitweise. Im nachfolgenden Bild sind es die beiden Zahlen A = 11001 und B=1101. Diese Eingabe erscheint auf dem Band des endlichen Automaten als eine Folge von 2-Bit-Worten. Das Ergebnis jeder Addition wird dann als Summe S von links nach rechts auf das Band geschrieben.
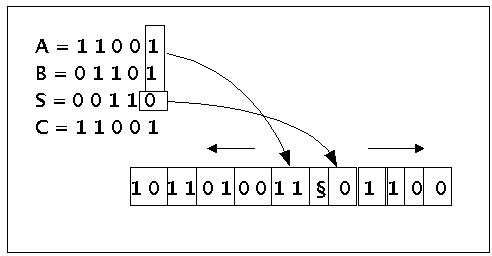
Beispielzahlen des Sequentiellen Automaten für Volladdition
Um jetzt diesen Zustandsgraphen in eine physikalische Schaltung umsetzen zu können, muss man zunächst die Funktionen F und G als Wertetabellen definieren. Dies geschieht direkt, indem man den Zustandsgraphen entsprechend in eine Tabelle umschreibt. Beispiel: wenn der Automat im Zustand Q=0 von der Zahl A eine 0 bekommt und von der Zahl B eine 0, dann ist der Folgezustand F(0,0,0) = 0 und die berechnete Summe G(0,0,0) = 0. usf.
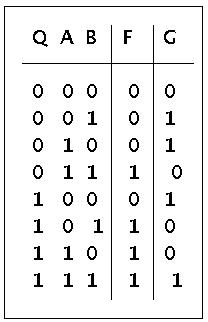
Funktionstabelle für F und G des Sequentiellen Automaten für Volladdition
Als nächstes müssen aufgrund dieser Wertetabellen für F und G boolsche Funktionen gefunden werden, die diesen Tabellen entsprechen. Folgende boolsche Funktionen sind möglich:
F = (Q & (B + A)) + (B & A) G = ((A XOR B) & ~Q) + (~(A XOR B) & Q)
Für diese boolschen Funktionen lässt sich eine konkrete Schaltung angeben, die die geforderte Aufgabe erfüllt:
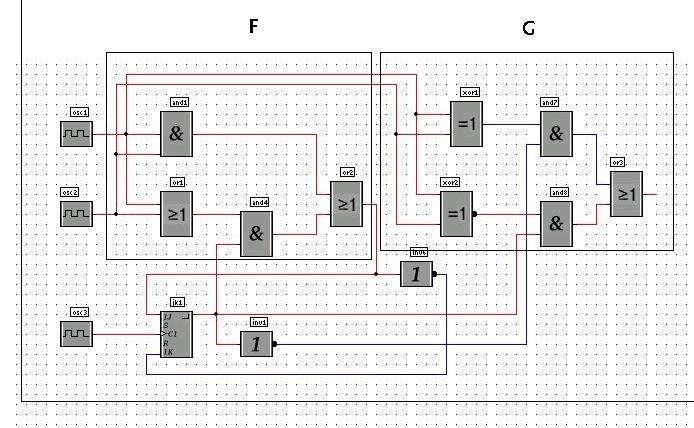
Sequentieller Automat für Volladdition
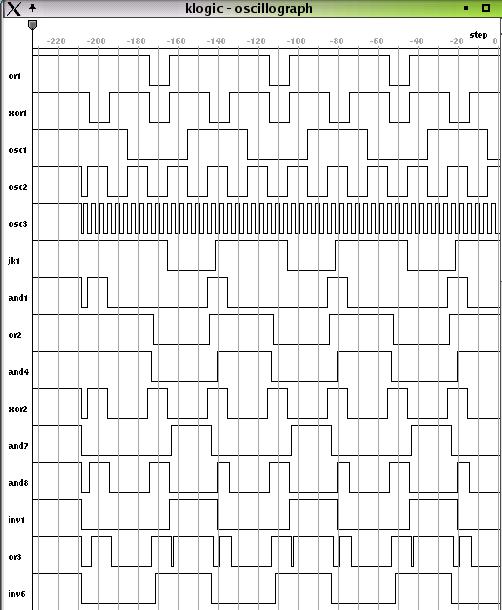
Oszillogramm des Sequentiellen Automaten für Volladdition
Die angegebenen boolschen Funktionen sind nicht in disjunktiver Normalform, da dies mehr Gatter erfordern würde.
Bilden sie ein Team von 5 Mitgliedern
Erstellung Sie gemeinsam einen Texte mit Namen und Matr.Nr. der AutorenInnen. Abgabe einer Kopie des Textes an den Dozenten vor Beginn der Übung.
Präsentation der Lösung als Team vor der gesamten Gruppe. Präsentationszeit (abhängig von der Gesamtzahl der Teams) 3-5 Min.
Versuchen Sie in dem Text Antworten auf folgende Aufgaben zu formulieren:
Verwandeln Sie den Ausdruck ~(((A + B) & ~B) + (C & B)) in eine disjunktive Normalform
Beschreiben Sie kurz die wichtigsten Eigenschaften von PHDs, PLEs, PALs, PLAs, PLSs, PMLs
Beschreiben sie die Struktur eines sequentiellen Automaten
Geben Sie ein Beispiel für einen sequentiellen Automaten mit einem Zustandsgraphen
Geben Sie ein Beispiel für die Berechnung des Folgezustands und des neuen Outputs eines endlichen Automaten.
Übersetzen Sie die logische Beschreibung eines endlichen Automaten in eine Schaltung.
Formen Sie die beiden Funktionen F und G des Volladdierers um in eine disjunktive Normalform und zeigen Sie, wie solch eine Schaltung aussehen würde.
Im vorausgehenden Beispiel mit dem Volladdierer wurden keine Endzustände benutzt. Beschreiben sie das Konzept eines endlichen Automaten als Volladdierer, der mit Endzzustnden arbeitet.