|
|
RECHNERARCHITEKTUR WS 0203 - Vorlesung mit Übung |
In der erstren Vorlesung wurde ein Zusammenhang aufgezeigt zwischen den Programmen und Algorithmen der täglichen Praxis und den notwendigen 'Akteuren', die solche Programme abarbeiten müssen. Akteure können Menschen sein oder geeignete Automaten. Als Repräsentant der Automaten wurde informell das Konzept einer Turingmaschine vorgestellt. Es wurde dann gefragt, wie man von diesem logischen Konzept eines Automaten zu einer physikalisch realisierten Maschine kommen kann, die die Eigenschaften eines solchen Automaten besitzt. Am Gang dr Technikentwicklung wurde verdeutlicht, wie die 'Zustände' eines Automaten sich durch technische Vorrichtungen immer besser realisieren lassen. Schliesslich wurde am Beispiel der modernen Transistoren gezeigt, wie sich damit Maschinenzustände als schaltbare logische Zustände realisieren lassen. Eine Querbeziehung zu biologischen Strukturen der Informationsverarbeitung (Neuron, Nervengewebe) wurde angedeutet.
In der heutigen Vorlesung wird es darum gehen, das Verständnis physikalisch realisierter Schaltlogik am Beispiel der modernen Transistortechnik weiter zu vertiefen. Nach einer kurzen Übersicht über die physikalischen Kennwerte einiger wichtiger Schaltungsfamilien wird das Konzept der Schaltalgebra (Boolschen Logik) eingeführt, es werden logische Zusammenhänge zwischen unterschiedlichen Schaltungen aufgezeigt, es werden Schaltungsbeispiele vorgestellt und es wird der Einfluss des Zeitfaktors in realen Schaltungen thematisiert.
In der letzten Vorlesung ist am Beispiel eines (pnp-)Tranistors als Schalter die Grundidee vermittelt worden, wie man mit einem Transistor einen 'Schalter' realisieren kann, der in dem speziellen Fall sogar noch das Signal invertierte. Ein als 'low' bezeichnetes Eingangssignal (an der Basis) wurde zu einem als 'high' bezeichneten Ausgangssignal am Kollektor, und umgekehrt.
Um die weiteren Überlegungen mit logischen Gattern zu verstehen, seien hier einige Grundbegriffe noch geklärt.
Zunächst muss festgelegt werden, welche physikalischen Werte den logischen Bezeichnungen 'high' bzw. 'low' (oder auch 'true' versus 'false' oder '1' versus '0') entsprechen sollen. in der sogenannten positiven Logik wird die Bezeichnung high dem Wert '+5V' (oder auch '+3.5V') zugeordnet und die Bezeichnung low dem Wert 0V. In der sogenannten negativen Logik ist dies genau umgekehrt.
Um Signalstörungen zu minimieren, wurden bestimmte Signalpegel vereinbart, so dass das H-Signal in einem vereinbarten Störabstand zum L-Signal liegt. Bei standard CMOS-Bausteinen liegt der verbotene Bereich z.B. zwischen +1.5V und +3.5V.
Ferner ist aufgrund physikalischer Gegebenheiten davon auszugehen, dass der Übergang von einem L-Zustand in einen H-Zustand eine gewisse Zeit benötigt. Diese Signalanstiegszeit ta wird gemessen zwischen 10% der Signalspannung und zwischen 90%. Entsprechend gibt es eine Signalabfallzeit tf sowie die eigentliche Signaldauer td.
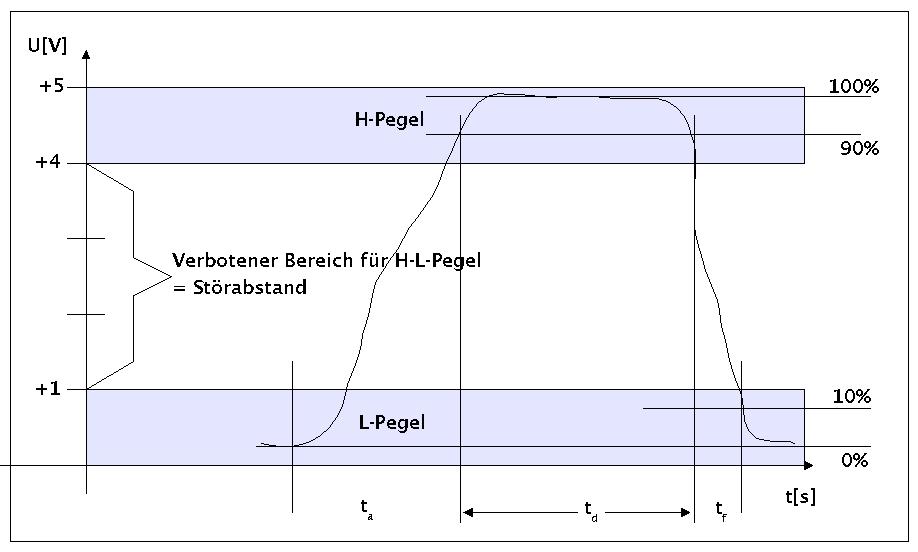
Logik-Signalpegel und Signalzeiten
Empfängt eine digitale Schaltstufe ein Signal, dann benötigt die Verarbeitung des Signals grundsätzlich auch Zeit, d.h. das Signal am Ausgang der Schaltstufe ist um eine gewisse Zeit verzögert. Diese Impulsverzögerungszeit td (d:= delay) wird einmal gemessen zwischen den Zeitpunkten, an denen die ansteigenden Flanken des Eingangssignals und des Ausgangssignals 50% ihrer maximalen Höhe erreicht haben (= td1) oder an jenen Zeitpunkten, an denen die abfallenden Flanken des Eingangs und des Ausgangssignals 50% ihrer maximalen Höhe erreicht haben (= td2).
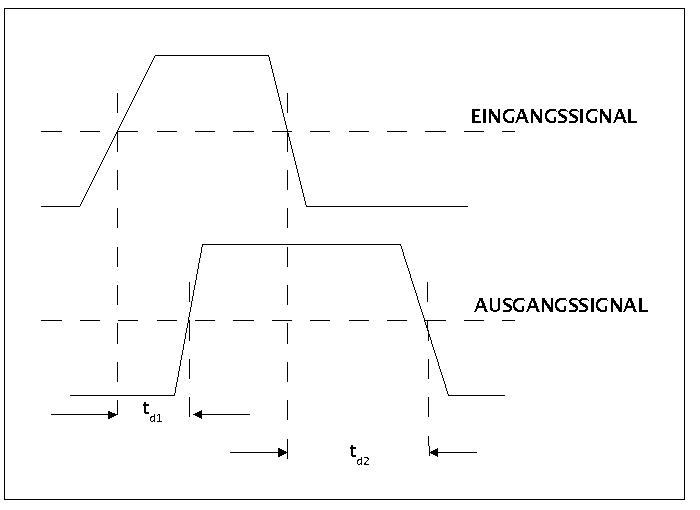
Signalverzögerung durch Gatterlaufzeiten
Eine andere wichtige Kenngrösse ist noch der Fan-out; dies ist die Anzahl der Eingänge von nachfolgenden Schaltstufen, die an einen Ausgang angeschlossen werden können. Der Fan-out liegt in der Regel mindestens bei 10, bei einer Reihe von Schaltkreisfamilien aber auch über 100.
Unbenutzte Eingänge von Schaltkreisen müssen grundsätzlich an die Betriebsspannung oder an Masse gelegt werden (oftmals über einen Schutzwiderstand).
Die wichtigsten Schaltkreisfamilien sind in unipolarer Technik die CMOS-Familie (mit verschiedenen Untergruppen) sowie in bipolarer Technik die TTL-Familie (mit sehr vielen Untergruppen) sowie die ECL-Familie. Für Details sei auf die entsprechende Literatur verwiessen.
Nachdem nun die Grundbegriffe für physikalische logische Schaltungen bereitgestellt sind, sollen jetzt jene logischen Funktionen kurz erläutert werden, die bei der Realisierung von logischen Schaltungen wichtig sind.
Ausgangspunkt ist die Tatsache, dass sich mit Gattern physikalisch Schaltungen realisieren lassen, die mit den Eingängen x1, ..., xn eine Funktion fi realisieren, deren Wert am Ausgang y erscheint. Nach Vereinbarungen können die Eingänge nur die Werte H (high) oder L (low) annehmen, entsprechend der Ausgang y. Danach hat man mit n-vielen Eingängen 2n-viele unterschiedliche Belegungen der Eingänge, denen man einen Wert für y zuordnen muss. Im Prinzip kann man dies über einfache Tabellen -mittels einer sogenannten Wahrheitswert-Tabelle- realisieren.
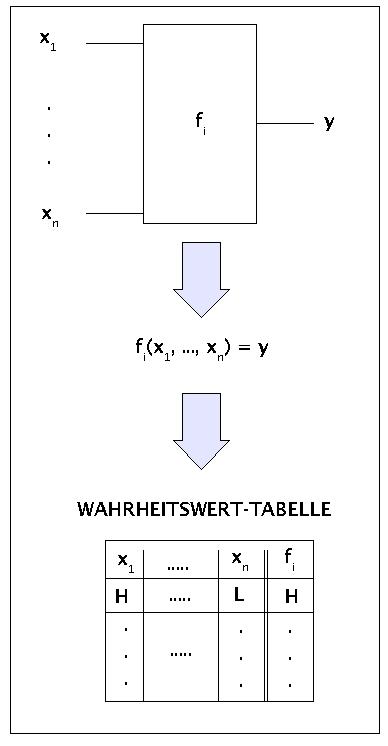
Beziehung zwischen Schaltfunktion und Wahrheitswerttabelle
Eine Wahrheitswert-Tabelle enthält für jeden Eingang eine Spalte und für jede Zeile der Tabelle, die einer möglichen Belegung aller Eingänge entspricht, legt man einen Funktionswert y fest.
x ist eine BOOLSCHE_LOGIK (BL): BL(x) iff x = < < BA, BV,BOOL>, BF > mit
BA ist die Menge der Boolschen Ausdrücke, BV ist die Menge der Boolschen Variablen, BOOL = {H,L}) und BF ist die Menge der Boolschen Funktionen, und es gilt:
Für jedes b in BF gilt: b ist eine Funktion und b in pow(BOOLn x BOOL)
Die Menge BV ist eine Teilmenge der Menge BA der Boolschen Ausdrücke
Wenn b in BF und x in BVn, dann ist b(x) auch ein Boolscher Ausdruck.
Nur was nach (i) und (ii) gebildet wurde, ist ein Boolscher Ausdruck.
Historisch war es der englische Mathematiker G.BOOLe, der 1854 solche Ausdrücke in seinem 'Treatise on the Laws of Human Thouht' systematisch untersucht hatte. Deswegen nennt man solch Ausdrücke auch 'Boolsche Ausdrücke'. Boolsche Ausdrücke haben eine direkte Beziehung zur Aussagenlogik (dier hier nicht weiter behandelt wird; siehe dazu die Vorlesung über Mathematik); im Falle der Aussagenlogik identifiziert man die Boolschen Ausdrücke mit aussagenlogischen Ausdrücken und die Boolschen Funktionen sind aussagenlogische Junktoren. Ferner kann man diese Sachverhalte auch mit den Ausdrucksmitteln eines mathematischen Verbandes analysieren.
In einer konkreten Boolschen Logik BL* muss man u.a. festlegen, welche konkreten Boolschen Funktionen gelten sollen. Fünf konkrete Boolsche Logiken BL1, ..., BL5 sind historisch und systematisch von Interesse.
In der Boolschen Logik BL1 sollen folgende drei Funktionen gelten:
f1 (Negation, '~'): f1(H) = L und f1(L) = H
f2 (AND, KONJUNKTION, UND, '&'): f2(H,H) = H, f2(L,H) = L, f2(H,L) = L, f2(L,L) = L
f3 (OR, DISJUNKTION, ODER, '+'): f3(L,L) = L, f3(H,H) = H, f3(H,L) = H,f3(L,H) = H
Schreibweisen: Statt 'f2(x,y)' kann man auch schreiben 'x & y' oder 'xy'. Entsprechend statt 'f3(x,y)' kann man auch schreiben 'x+y'. Statt 'f1(x) schreibt man auch '~x' oder 'x' mit einem Schrägstrich über dem x (in HTML noch nicht darstellbar). Treten alle Funktionen in einem Ausdruck auf, dann gelten die Prioritäten '~ > & > +'.
Im zuvor zitierten Werk von G.BOOL konnte BOOL den Satz beweisen, dass sich alle n-stelligen Boolschen Funktionen auf eine Kombination aus den drei Funktionen BF1 = {f1,f2,f3} zurückführen lassen. Dies bedeutet, dass die Menge BF1 logisch vollständig ist.
Da die folgenden Gleichungen gelten:
kann man die Logik BL1 noch vereinfachen zu den Logiken BL2 oder BL3:
In der Boolschen Logik BL2 sollen folgende zwei Funktionen gelten:
f1 (Negation, '~'): f1(H) = L und f1(L) = H
f2 (AND, KONJUNKTION, UND, '&'): f2(H,H) = H, sonst f2() = L
In der Boolschen Logik BL3 sollen folgende zwei Funktionen gelten:
f1 (Negation, '~'): f1(H) = L und f1(L) = H
f3 (OR, DISJUNKTION, ODER, '+'): f3(L,L) = L, sonst f3() = H
Anmerkung: Wir behalten in BL2 und BL3 die Nummerierung der Boolschen Funktionen mit f2 bzw. f2 aus dem vorausgehenden Beispiel bei.
Aus der Geschichte der Aussagenlogik ist bekannt, dass man die Anzahl der Funktoren bis auf einen verringern kann. Eine Variante geht zurück auf den russisch gebürtigen amerikanischen Mathematiker H.M.Sheffer (1883 - 1964), der 1913 bewiessen hat, dass man mit einem 'Negatdisjunktor' ''|' := ~(x & y)' (=NAND)(der sogenannte Sheffersche Strich) alle anderen Boolschen Funktoren herleiten kann.
In der Boolschen Logik BL4 (Sheffersche Logik)soll folgende Funktion gelten:
f4 (NAND, SHEFFERSCHER STRICH,NEGIERTES UND; '|'): f4(L,L) = H, sonst f3() = L
Historisch soll aber Ch.S.PEIRCE schon lange vor SHEFFER entdeckt haben, dass man eine Aussagenlogik mit nur einem Junktor realisieren kann. Der Peircesche Junktor ist dual zu Sheffers Strich: '\|/ := ~(x + y)' (NOR).
In der Boolschen Logik BL5 (Peircesche Logik) soll folgende Funktion gelten:
f5 (NOR, PEIRCESCHER OPERATOR, NEGIERTES ODER; '\|/'): f5(L,L) = H, sonst f3() = L
Wie schon erwähnt, kann man die Boolsche Logik auch mit den Mitteln eines mathematischen Verbandes analysieren, in dem die Distributivgesetze gelten, insbesondere gilt 'xy + xz = x(y + z)'. Ferner zeigt sich, dass AND und OR dual zueinander sind; man kann Formeln mit AND in Formeln mit OR umwandeln, indem man die Wahrheitswerte invertiert:
|
GESETZ |
AND-Form |
OR-FORM |
|---|---|---|
|
Identitätsgesetz |
1A = A |
0 + A = A |
|
Nullgesetz |
0A = 0 |
1 + A = 1 |
|
Idempotenzgesetz |
AA = A |
A + A = A |
|
Inversionsgesetz |
A & ~A = 0 |
A + ~A = 1 |
|
Kommutativgesetz |
AB = BA |
A + B = B + A |
|
Assoziativgesetz |
(AB)C = A(BC) |
(A + B) + C = A + (B + C) |
|
Distributivgesetz |
A + BC = (A + B)(A + C) |
A(B + C) = AB + AC |
|
Absorptionsgesetz |
A(A + B) = A |
A + AB = A |
|
De Morgansche Gleichungen |
~(AB) = ~A + ~B |
~A + ~B = ~(AB) |
|
De Morgansche Gleichungen |
~A & ~B = ~(A + B) |
~(A + B) = ~A & ~B |
Für die spätere Anwendung in komplexen logischen Schaltungen -sogenannten 'Programmierbaren Logikbausteinen (siehe dort)- ist es hilfreich, sich auch mit den sogenannten aussagenlogischen Normalformen vertraut zu machen. Insbesondere benutzt man die Konjunktive Normalform (KNF) oder die Disjunktive Normalform (DNF)
Ein Ausdruck ist in der Konjunktive Normalform (KNF) wenn er nur die Boolschen Funktionen '~', '&' und '+' enthält und es gilt, dass im Klammerbereich der Negation '~' keine andere boolsche Funktion mehr auftritt (auch kein zweites Negationszeichen '~') und wenn im Klammerbereich von jedem Disjunktionszeichen '+' kein Undzeichen '&' auftritt. Man hätte also Ausdrücke der Form E1 & ... & Ek und jedes Ei wäre von der Form X1 + ... + Xm mit Xj eine Boolsche Variable 'A' oder deren Negation '~A'.
Ein Ausdruck ist in der Disjunktiven Normalform (DNF) wenn er nur die Boolschen Funktionen '~', '&' und '+' enthält und es gilt, dass im Klammerbereich der Negation '~' keine andere boolsche Funktion mehr auftritt (auch kein zweites Negationszeichen '~') und wenn im Klammerbereich von jedem Konjunktionszeichen '&' kein Oderzeichen '+' auftritt. Man hätte also Ausdrücke der Form E1 + ... + Ek und jedes Ei wäre von der Form X1 & ... & Xm mit Xj eine Boolsche Variable 'A' oder deren Negation '~A'.
Man kann beweisen, dass sich jeder boolsche Ausdruck äquivalent in eine der beiden Normalformen umformen lässt.
Eine mögliche Umformungsvorschrift für Disjunktive Normalformen ist die folgende:
Gegeben sei ein Ausdruck, der nur die Funktionen '~', '&' und '+' enthält.
Das Negationszeichen wird solange 'nach innen' geschoben, bis jedes Negationszeichen nur noch eine einzelne Aussagenvariable bindet. Man benutzt dazu die Äquivalenzen: '~(A & B) gdw ~A + ~B)' und '~(A + B) gdw ~A & ~B' und '~~A gdw A'.
Es muss jetzt das Funktionszeichen '&' so verschoben werden, dass im Klammerbereich von '&' kein Disjunktionszeichen '+' mehr auftritt. Dazu benutzt man die Äquivalenzen: 'A & (B + C) gdw (A & B)+(A & C)' sowie '(A + B) & C gdw (A & C)+(B & C)'
Beispiel:
~( ( (A + B) & ~B ) + (C & B) )
Negation nach innen~((A + B) & ~B) & ~(C & B)
Negation nach innen(~(A + B) + ~~B) & (~C + ~B)
Negation nach innen(( ~A & ~B) + B) & (~C + ~B)
Konjunktion schieben( ~A & ~B)& (~C + ~B) + (B & (~C + ~B)
Konjunktion schieben( ~A & ~B & ~C) + ( ~A & ~B) + (B & ~C) + (B & ~B)
Die formale Symmetrie der beiden Normalformen ist augenfällig und man spricht hier von dualen Formen. Dabei ist unter dem zu einem Ausdruck A* dualen Ausdruck derjenige Ausdruck B* zu verstehen, der aus A* dadurch entsteht, dass die Zeichen der Boolschen Funktionen '+' und '&' gegeneinander ausgetauscht werden. Zum Beispiel gehört zum Ausdruck
~((A & B) + ~C)
der duale Ausdruck:
~((A + B) & ~C)
Es lässt sich folgender Dualitäts-Satz beweisen (siehe dazu auch [HILBERT/ ACKERMANN 1972:19f]): "Ist A* eine Aussageform, die sich die sich nur mit Hilfe von '~', '+' und '&' aufbaut, so erhalten wir eine zu '~A*' äquivalente Aussageform, indem wir von A* zur dualen Aussageform übergehen, und darin jede Aussagevariable, die nicht unmittelbar negiert vorkommt, durch die negierte Aussagenvariable und jede negierte Aussagevariable, durch die einfache ersetzten"
So gehört also zum Ausdruck
~((A & B) + ~C)
der duale Ausdruck:
~((A + B) & ~C)
und es gilt dann die Äquivalenz:
~~((A & B) + ~C) gdw ~((~A + ~B) & C)
Es wird jetzt anhand von einfachen Boolschen Funktionen gezeigt, wie diese zu realisieren sind:
A + B & C
(A + B)(A + C)
A(B + C)
AB + AC
A(A + B)
~(AB)
~(A + B)
~(~A & ~B)
~(A & ~B)
Bilden sie ein Team von 5 Mitgliedern
Erstellung Sie gemeinsam einen Texte mit Namen und Matr.Nr. der AutorenInnen. Abgabe einer Kopie des Textes an den Dozenten vor Beginn der Übung.
Präsentation der Lösung als Team vor der gesamten Gruppe. Präsentationszeit (abhängig von der Gesamtzahl der Teams) 3-5 Min.
Versuchen Sie in dem Text Antworten auf folgende Aufgaben zu formulieren:
Entwickeln Sie wenigstens ein Beispiel, in dem eine Schaltung mit 5 Gattern vorkommt, die dann durch äquivalente Schaltungen mit weniger Gattern ersetzt wird. Geben Sie die zugehörigen boolschen Funktionen sowohl in Formelschreibweise an wie auch in Diagrammschreibweise .
Ein bekannter Junktor ist auch die ausagenlogische Implikation (Zeichen: '=>'), bekannt auch als 'Wenn ... dann
...', mit (A => B) = (~A + B) bzw. ~(A & ~B). 'A => B' gesprochen: Wenn A dann B. Formen Sie folgende
umgangssprachlichen Ausdruck unter Verwendung des Operators '=>' in einen boolschen Ausdruck um:
"Wenn kein Feuer
ausbricht, dann kann Peter zu Hause bleiben, dann hat die Feuerwehr Feierabend."
Übersetzen Sie diesen Ausdruck mit dem
Operator '=>' in einen boolschen Ausdruck ohne den Operator '=>' um. Geben Sie dazu auch eine Schaltung an.
Es sei angenommen, dass die Gatter, die Sie in ihren vorausgehenden Schaltungen verwenden, eine Gatterlaufzeit von 2 ns [Nanosekunden] haben während die Signallaufzeit auf den normalen Leitungen mit 0 ns angenommen wird. Stellen Sie fest, ob durch diese Gatterlaufzeiten die Logik ihrer Schaltungen eventuell gestört wird.