From the preceding introduction we can try to abstract a formal structure which represents - hopefully - all the key properties which are necessary to describe the behavior of self-organizing systems as generally as possible in a way that all the interesting details of concrete adaptive biological systems can be included if needed. This structure is intended as framework for the following more elaborated formalizations of genetic algorithms without and with a phenotype (cf. figure 4.1):
Figure 4.1:
Genetic Loop of Evolutionary Framework of Engineered Intelligent Systems
|
![\includegraphics[width=5.0in]{EvolutionaryFrameworkModel1.eps}](img150.png) |
- Environment: All systems
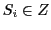 are presupposed to be located in an environment
are presupposed to be located in an environment 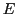 which can change. These changes can be mapped onto a time-line
which can change. These changes can be mapped onto a time-line 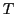 .
.
- Systems: Every system
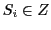 is an input-output system with a system function
is an input-output system with a system function
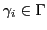 mapping input
mapping input
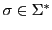 into output
into output
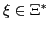 as
as
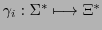 . Every system
. Every system 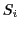 also possesses at least one blueprint ('genotype')
also possesses at least one blueprint ('genotype')
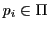 of it's structure, which can be used for the formation of new blueprints.
of it's structure, which can be used for the formation of new blueprints.
- Life-Time: A living system
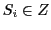 has a finite duration characterized by a start time
has a finite duration characterized by a start time 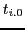 ('birth') and an end time
('birth') and an end time 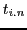 ('death'). The life-time of a living system is therefore given by the pair
('death'). The life-time of a living system is therefore given by the pair
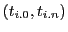 .
.
- Mating-Function: From a certain point of time during their lifetime
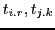 two living systems
two living systems
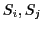 can produce a new blueprint ('genotype')
can produce a new blueprint ('genotype')
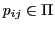 of a new system using their built-in blueprints
of a new system using their built-in blueprints
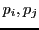 by applying a mating function
by applying a mating function
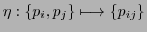 . Every new blueprint ('genotype')
. Every new blueprint ('genotype') 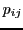 is assumed to be in a storage unit
is assumed to be in a storage unit
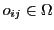 from which it can be delivered to built up a new system4.1
from which it can be delivered to built up a new system4.1
- Growth-Function, Phenotype: The growth-function
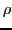 can take a blueprint
can take a blueprint 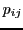 from a storage unit
from a storage unit 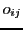 and can built up a new system ('gphenotype')
and can built up a new system ('gphenotype')
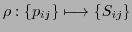 . The time to grow is an initial part of the life-time of a system represented as
. The time to grow is an initial part of the life-time of a system represented as
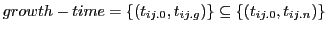 with
with
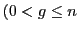 ). During the growth-time of a system the system
). During the growth-time of a system the system 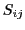 is assumed to begin functioning as far as the system-function
is assumed to begin functioning as far as the system-function
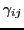 can do anything.4.2
can do anything.4.2
- Learning-Capacity: The system-function
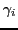 of a living system
of a living system 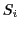 is assumed to be adaptive, i.e. it is assumed that this function can learn. Learning is defined with regard to the observable behavior of the system: If the behavior of a system
is assumed to be adaptive, i.e. it is assumed that this function can learn. Learning is defined with regard to the observable behavior of the system: If the behavior of a system 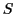 after some point of time
after some point of time 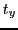 is better than before some point of time
is better than before some point of time 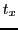 (with
(with 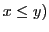 then the system
then the system 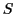 is classified as having improved and this is assumed to be the result of some learning based on internal changes of the system-function
is classified as having improved and this is assumed to be the result of some learning based on internal changes of the system-function 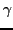 . The usage of the term 'better' presupposes the availability of an operational criterion which can be applied to the observable behavior and which can be measured in an objective way. Example: the measurable time to find food in a certain environment is becoming 'shorter' after time
. The usage of the term 'better' presupposes the availability of an operational criterion which can be applied to the observable behavior and which can be measured in an objective way. Example: the measurable time to find food in a certain environment is becoming 'shorter' after time 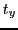 than 'before'
than 'before' 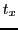 .
.
Gerd Doeben-Henisch
2013-01-14