Update of Outgoing Weights

$$W_{J}(t+1) = W_{J}(t) + \eta2 * A_{j} * E_{o}$$ (8.11)

$$E_{o} = O_{d} - O_{c}$$ (8.12)

$$O_{c} = \langle A_{o.1}, \cdots , A_{o.k}\rangle$$ (8.13)

$$A_{n} = 1 - D_{I.j}$$ (8.14)

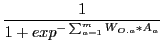$$A_{o} = \frac{1}{1+exp^{-\sum_{a=1}^{m} W_{O.a}*A_{a}}}$$ (8.15)

The weight vector $W_{J}$ at $t+1$ is the result of the summation of the weight vector $W_{J}$ at $t$ and the product of the learning constant $\eta2$ with the activation value of the evolving neuron $j$ and the error vector $E_{o}$. The calculated output vector $O_{c}$ contains all the output activations $A_{o.i}$. The output activation is in the cited papers of Watts and Kasabov not clearly defined. We are using here a sigmoid function which takes as exponent the sum of the product of the weight vector of all weights connected to an output neuron $o$ from $m-many$ connected evolving neurons, where each sending neuron has the activity $A_{a}$. Additionally one has to use some threshold if the gvalues of $O_{d}$ are all binary.

A more detailed description of the SECoS as well as discussion of its properties can be found in the application examples below.