Matrizen

Die Menge $MTX$ der Matrizen ist ganz allgemein eine strukturierte Menge über der Menge $V \times Nat \times Nat$, also

$$MTX \subseteq V \times Nat \times Nat$$ (8.32)

mit $V$ als einer Menge von Werten ('values') und der Menge der natürlichen Zahlen $Nat$ als Indexmenge. Sei $\textbf{M} \in MTX$ dann gilt für jedes Element $m_{i.j} \in \textbf{M}$ daß das erste Element $i$ ein Index aus einem Anfangsabschnitt der natürlichen Zahlen ist, der eine Zeile ('row') repräsentiert und daß das zweite Element $j$ ebenfalls ein Index aus einem Anfangsabschnitt der natürlichen Zahlen ist, der eine Spalte ('column') repräsentiert. Sei $m = \mid\{i \mid m_{i.j} \in \textbf{M} \}\mid$ die Anzahl der Zeilen der Matrix M und $n = \mid\{j \mid m_{i.j} \in \textbf{M}\}\mid$ die Anzahl der Spalten, dann spricht man bei der Matrix M auch von einer $m\times n$-Matrix.

Matrizen werden meistens mit großen Buchstaben benannt. Im Beispiel mit den M-, N- und P-Matrizen stellt M eine Matrix mit 3 Spalten und 2 Zeilen vor, also eine $2 \times 3$-Matrix, N eine $3 \times$-Diagonal-Matrix und P eine $3 \times$-Symmetrische-Matrix. Eine Diagonal-Matrix, die nur aus 1-en besteht, nennt man eine Identitäts-Matrix.

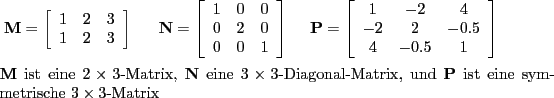
Addition mit Skalar: Wenn ein Skalar $a \in \Re$ zu einer Matrix M mit Werten aus $\Re$ addiert werden soll, dann liegt der Fall vor:

$$\textbf{U} = a + \textbf{M}$$ (8.33)

$$\forall u_{i.j}\in \textbf{U},\forall m_{i.j} \in \textbf{M} : u_{i.j} = a + m_{i.j}$$ (8.34)

$$\begin{eqnarray*} \left[\begin{array}{ccc} 4 & 5 & 6\\ 7 & 8 & 9 \end{array}\ri... ...eft[\begin{array}{ccc} 1 & 2 & 3\\ 4 & 5 & 6 \end{array}\right] \end{eqnarray*}$$

Subtraktion mit Skalar: Wenn ein Skalar $a \in \Re$ von einer Matrix M mit Werten aus $\Re$ subtrahiert werden soll, dann liegt der Fall vor:

$$\textbf{U} = \textbf{M} - a$$ (8.35)

$$\forall u_{i.j}\in \textbf{U},\forall m_{i.j} \in \textbf{M} : u_{i.j} = m_{i.j} - a$$ (8.36)

$$\begin{eqnarray*} \left[\begin{array}{ccc} 1 & 2 & 3\\ 4 & 5 & 6 \end{array}\ri... ...\begin{array}{ccc} 4 & 5 & 6\\ 7 & 8 & 9 \end{array}\right] - 3 \end{eqnarray*}$$

Multiplikation mit Skalar: Wenn ein Skalar a mit einer Matrix M multipliziert werden soll, dann liegt der Fall vor:

$$\textbf{U} = a\cdot\textbf{M}$$ (8.37)

$$\forall u_{i.j}\in \textbf{U},\forall m_{i.j} \in \textbf{M} : u_{i.j} = a * m_{i.j}$$ (8.38)

$$\begin{eqnarray*} \left[\begin{array}{ccc} 3 & 6 & 9\\ 12 & 15 & 18 \end{array... ...eft[\begin{array}{ccc} 1 & 2 & 3\\ 4 & 5 & 6 \end{array}\right] \end{eqnarray*}$$

Addition zweier Matrizen: Wenn eine Matrix M mit einer Matrix N addiert werden soll, dann liegt der Fall vor:

$$\textbf{U} = \textbf{M}+\textbf{N}$$ (8.39)

$$\forall u_{i.j}\in \textbf{U},\forall m_{i.j} \in \textbf{M},\forall n_{i.j} \in \textbf{N} : u_{i.j} = m_{i.j} + n_{i.j}$$ (8.40)

$$\begin{eqnarray*} \left[\begin{array}{ccc} 2 & 3 & 4\\ 6 & 7 & 8 \end{array}\ri... ...eft[\begin{array}{ccc} 1 & 1 & 1\\ 2 & 2 & 2 \end{array}\right] \end{eqnarray*}$$

Subtraktion zweier Matrizen: Wenn eine Matrix N von einer Matrix M subtrahiert werden soll, dann liegt der Fall vor:

$$\textbf{U} = \textbf{M}-\textbf{N}$$ (8.41)

$$\forall u_{i.j}\in \textbf{U},\forall m_{i.j} \in \textbf{M},\forall n_{i.j} \in \textbf{N} : u_{i.j} = m_{i.j} - n_{i.j}$$ (8.42)

$$\begin{eqnarray*} \left[\begin{array}{ccc} 1 & 2 & 3\\ 4 & 5 & 6 \end{array}\ri... ...eft[\begin{array}{ccc} 1 & 1 & 1\\ 2 & 2 & 2 \end{array}\right] \end{eqnarray*}$$

Elementweise Multiplikation zweier Matrizen (Hadamard Produkt): Wenn eine Matrix M mit einer Matrix N elementweise multipliziert -Zeichen $.*$- werden soll, dann liegt der Fall vor:

$$\textbf{U} = \textbf{M} .* \textbf{N}$$ (8.43)

$$\forall u_{i.j}\in \textbf{U},\forall m_{i.j} \in \textbf{M},\forall n_{i.j} \in \textbf{N} : u_{i.j} = m_{i.j} * n_{i.j}$$ (8.44)

$$\begin{eqnarray*} \left[\begin{array}{ccc} 2 & 4 & 6\\ 8 & 10 & 12 \end{array}\... ...eft[\begin{array}{ccc} 2 & 2 & 2\\ 2 & 2 & 2 \end{array}\right] \end{eqnarray*}$$

Multiplikation eines Vektors mit einer Matrix (Inneres Produkt): Wenn ein Vektor v mit einer Matrix M als inneres Produkt multipliziert -Zeichen $*_{ip}$- werden soll, dann wird ein neuer Vektor u erzeugt:

$$\textbf{u} = \textbf{v} *_{ip} \textbf{M}$$ (8.45)

$$\forall i \in length(v),\forall j \in col(M): u_{j} = \sum_{i}^{length(v)} v_{i} * m_{i.j}$$ (8.46)

$$\begin{eqnarray*} \left[\begin{array}{ccc} 18 & 23 & 28 \end{array}\right] & = &... ...ray}{ccc} 1 & 2 & 3\\ 4 & 6 & 8\\ 3 & 3 & 3 \end{array}\right] \end{eqnarray*}$$