Next: Matrizen Up: Mathematischer Anhang Previous: Mathematischer Anhang Contents
Vektor: Ein Vektor ist ein Element aus einem n-fachen kartesischen Produkt
Addition von zwei Vektoren: Zwei Vektoren v,v' gleicher Länge lassen sich wie folgt addieren:
Subtraktion von zwei Vektoren: Zwei Vektoren v,v' gleicher Länge lassen sich wie folgt subtrahieren:
Multiplikation mit Skalar: Ein Vektor v läßt sch mit einem Skalar ![]() multiplizieren:
multiplizieren:
Kollineare Vektoren: Zwei Vektoren v,v' gleicher Länge sind kollinear zueinander, wenn ![]() und es gilt:
und es gilt:
Linear erzeugbare Vektoren: Ein Vektor v gilt als linear erzeugbar aus den Vektoren
![]() wenn es gleichviele Skalare
wenn es gleichviele Skalare
![]() gibt, so daß gilt:
gibt, so daß gilt:
Linear unabhängige Vektoren: Eine Menge von Vektoren
![]() gilt als linear unabhängig wenn keiner der Vektoren
gilt als linear unabhängig wenn keiner der Vektoren
![]() aus den anderen Vektoren linear erzeugbar ist.
aus den anderen Vektoren linear erzeugbar ist.
n-dimensionaler Vektorraum: n-linear unabhängige Vektoren spannen einen n-dimensionalen Vektorraum auf. Die n linear unabhängigen Vektoren werden auch die Basis dieses Vektorraumes genannt.
Satz: In einem n-dimensionalen Vektorraum kann es nicht mehr als n-viele linear unabhängige Vektoren geben.
Satz: Seien die Vektoren
![]() die n-dimensionale Basis eines Vektorraumes mit
die n-dimensionale Basis eines Vektorraumes mit
![]() , dann gilt, daß jeder andere Vektor v dieses Raumes sich als eine Linearkombination über den Einheitsvektoren darstellen läßt, also
, dann gilt, daß jeder andere Vektor v dieses Raumes sich als eine Linearkombination über den Einheitsvektoren darstellen läßt, also
Inneres Vektorprodukt (auch Skalarprodukt) Das innere Produkt -Zeichen ![]() oder
oder ![]() oder
oder ![]() - von zwei Vektoren v,w ist die Summe der Produkte der Einzelkomponenten, also
- von zwei Vektoren v,w ist die Summe der Produkte der Einzelkomponenten, also
Basisvektoren Die einzelnen Werte eines Vektors repräsentieren Skalare, die mit dem jeweiligen Basisvektor ![]() multipliziert werden, also
multipliziert werden, also
![]() und
und
![]() gilt:
gilt:
Länge -oder Norm- eines Vektors: Mit Vektor v gilt:
![\fbox{
\parbox{4.5in}{
v=[1 2]\\
norm(v) = 2.236068
}}](img443.png)
Einheitsvektor: Will man alle Werte auf den Wertebereich [0,1] normieren, dann sprich man von einem Einheitsvektor angezeigt durch ein aufgesetztes Caret, wie z.B. ![]() . Der normalisierte Vektor oder versor
. Der normalisierte Vektor oder versor ![]() eines von Null verschiedenen Vektors u ist der Einheitsvektor, der mit u kodirektional ist.
eines von Null verschiedenen Vektors u ist der Einheitsvektor, der mit u kodirektional ist.
| (8.13) |
wobei
![]() die Norm oder Länge von u genannt wird. Die Begriffe normalisierter Vektor und Einheitsvektor werden of synonym gebraucht.
die Norm oder Länge von u genannt wird. Die Begriffe normalisierter Vektor und Einheitsvektor werden of synonym gebraucht.
![\fbox{
\parbox{4.5in}{
v=[1 2]\\
norm(v) = 2.236068\\
$\hat{v}$=$\frac{v}{norm(v)}$\\
$\hat{v}$ = [0.4472136 0.8944272]
}}](img449.png)
Anmerkung: Will man die relativen Abstände erhalten, muß man allerdings alle Vektoren auf eine einzige Norm beziehen, sinnvollerweise auf die größte Norm aller beteiligten Werte.
-->INP
INP =
1. 2.
1. 3.
2. 2.
2. 3.
4. 4.
4. 5.
5. 4.
5. 5.
6. 1.
6. 2.
7. 1.
7. 2.
INP3=doNormU(INP)
INP3 =
0.1373606 0.2747211
0.1373606 0.4120817
0.2747211 0.2747211
0.2747211 0.4120817
0.5494423 0.5494423
0.5494423 0.6868028
0.6868028 0.5494423
0.6868028 0.6868028
0.8241634 0.1373606
0.8241634 0.2747211
0.9615239 0.1373606
0.9615239 0.2747211
function [INP3]=doNormU(INP)
[r,c] = size(INP)
Maxnorm=0
INP3=[]
//Looping through the input to find maximal norm
for i=1:r
v=[INP(i,1) INP(i,2)]
if norm(v) > Maxnorm then Maxnorm=norm(v)
end
end
//Looping through the input to normalize uniformly
for i=1:r
v=[INP(i,1) INP(i,2)]
v=v/Maxnorm
INP3(i,1)=v(1)
INP3(i,2)=v(2)
end
endfunction
![\includegraphics[width=2.5in]{inp_normal_inp3_normalized_2.5inch.eps}](img450.png) |
Satz: Mit Vektoren v, v', Skalar ![]() , und Null '0' gilt:
, und Null '0' gilt:
Winkel zwischen Vektoren Mit Vektoren v,w und Winkel ![]() kann man definieren (Winkel im Bogenmaß
kann man definieren (Winkel im Bogenmaß ![]() :
:

Orthogonale Vektoren: Wenn ein Vektor v senkrecht (orthogonal) auf einem anderen Vektor w steht, soll dies geschrieben werden:
Satz: Zwei Vektoren v, w sind orthogonal zueinander, wenn ihr Skalarprodukt gleich Null '0' ist
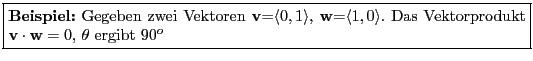
Satz: Orthohonalität impliziert Lineare Unabhängigkeit, nicht umgekehrt.
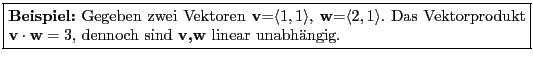
Projektion von v auf l im Winkel ![]() : Wenn ein Vektor v im Winkel
: Wenn ein Vektor v im Winkel ![]() zu einer Geraden l steht, dann fällt der projizierte Abschnitt x von v auf l um so größer (kleiner) aus, umso kleiner (größer) der Winkel
zu einer Geraden l steht, dann fällt der projizierte Abschnitt x von v auf l um so größer (kleiner) aus, umso kleiner (größer) der Winkel ![]() ist:
ist:

Gerd Doeben-Henisch 2013-01-17