|
|
I-TI04 Theoretische Informatik WS04
|
In dieser VL werden auf der Basis der Formalisierung der Turingmaschine und der wichtigsten Grundbegriffe der formalen Sprachen einige weitere wichtige Begriffe eingeführt: akzeptierte Sprache, Entscheidungsverfahren und entscheidbare Sprache
STARTVoraussetzung für die folgenden Begriffe ist der Begriff der turingberechenbaren Funktion. In einer vorausgehenden Vorlesung wurde schon definiert, was es heisst, dass eine Konfiguration k' aus einer Konfiguration k mit einer Turingmaschine m ableitbar ist. Man kann dafür schreiben:
k |--*m k'
Sei z.B. k = q0w eine Startkonfiguration und k' = aqevb eine Endkonfiguration mit der Konvention a,w ∈ G*, v ∈ (G\{§})*, qe ∈ E und b = ε oder b = §x mit x ∈ G*. Dann würde dies bedeuten, dass die Turingmaschine m beginnend mit dem Inputwort w nach endlich vielen Schritten in einem Endzustand qe anhält, wobei links von der aktuellen Position mit a irgendeine Zeichenkombination stehen kann, ab der aktuellen Position nach rechts ein Ergebniswort v ohne Leerzeichen und hinter dem Ergebniswort v entweder nichts oder ein Blank § gefolgt von einem Wort x.
Man kann diesen Sachverhalt auch so darstellen, dass man sagt, dass die Turingmaschine m eine Abbildung f vornimmt von A* nach (G\{§})*, also:
fm: A* --> (G\{§})*
Insofern die Funktion fm für jeden Wert aus A* nach endlich vielen Schritten einen eindeutigen Wert aus (G\{§})* liefert, soll sie eine totale Funktion heissen. Liefert die Funktion fm nicht nach endlich vielen Schritten für alle Werte aus A* einen eindeutigen Wert aus (G\{§})*, dann soll die Funktion fm eine partielle Funktion heissen. In diesem undefinierten Fall schreibt man auch fm(w) = ⊥ mit w ∈ A*.
Nach diesen Vorarbeiten kann man folgendes definieren:
Seien A und B zwei Alphabete und sei f eine partielle Funktion mit
f: A* --> B*
Die Fuktion f heisse genau dann turingberechenbar, wenn es eine Turingmaschine m mit dem Eingabealphabet A gibt, einem Bandalphabet G, dem leeren Zeichen §, sodass B C G\{§}, w ∈ A* und
f(w) = fm(w).
Nachdem nun die Turingmaschine eingeführt worden ist und mit ihr der Begriff der turingberechenbaren Funktion kann man die Turingmaschine nun benutzen, um Entscheidungsverfahren zu etablieren bzw. um überhaupt dem Begriff der Entscheidbarkeit eine Präzision zu verleihen.
Das nachfolgende Schaubild gibt die allgemeine Problemstellung wieder.
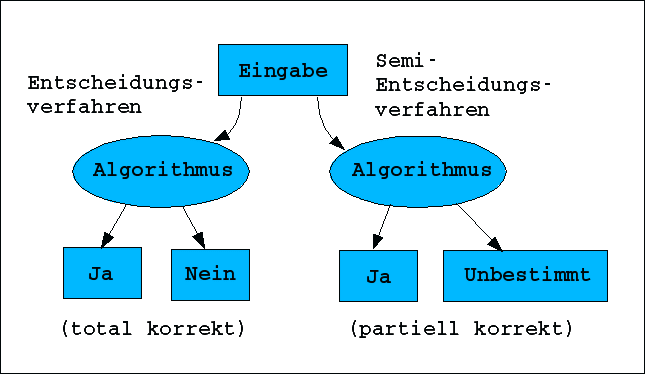
Entscheidungsverfahren
Ein Entscheidungsverfahren liegt vor, wenn es ein allgemeines Verfahren, also einen Algorithmus, gibt, der bei Eingabe eines Problems nach endlich vielen Schritten entweder mit "JA" antwortet oder mit "Nein". Antwortet das Verfahren immer nur in den Ja-Fällen umfassend und korrekt, nicht aber in den Nein-Fällen, dann spricht man von einem Semientscheidungsverfahren.
Um diesen Sachverhalt zu beschreiben wurde auch der Begriff der charakteristischen Funktion geprägt. Sei L C A* eine Sprache, in der sich das zu entscheidende Problem ausdrücken lässt. Dann soll χL die totale charakteristische Funktion sein mit:
χL: A* --> {0,1}
χL(w) = 1, falls w ∈ L
χL(w) = 0, falls w ∉ L
Entsprechend für den Fall einer partiellen charakteristische Funktion mit:
χL: A* --> {⊥,1}
χL(w) = 1, falls w ∈ L
χL(w) = ⊥, sonst
Folgende Sätze lassen sich dann --auch unter Rückgriff auf die Definitionen aus VL3 (akzeptierte Sprache, verworfene Sprache, entscheidbare Sprache, semientscheidbare Sprache usw.) beweisen:
Sei L C A* und ¬L = A*\L, dann gilt:
L ist entscheidbar gdw die totale charakteristische Funktion χL turingberechenbar ist.
L ist semientscheidbar gdw die partielle charakteristische Funktion χL turingberechenbar ist.
L ist entscheidbar gdw ¬L ist entscheidbar
L und ¬L ist semientscheidbar gdw L ist entscheidbar
| BEWEIS ZU |
| ---> |
A1: SDEC(L,A,m) & SDEC(¬L,A,m) |
| <--- |
A1:DEC(L,A,m) |
Aufzählbar (rekursive aufzählbar, semientscheidbar): eine Menge M ist aufzählbar, falls es eine surjektive Funktion f: Nat ---> M gibt, und f ist eine turingberechenbare Funktion.
Aufzählung von M: ist die Menge M aufzählbar und ist f die turingberechenbare Funktion zu M, dann ist die Folge <f(0), f(1), ... > eine Aufzählung von M
Satz: Jede endliche Menge ist aufzählbar. Sei M eine endliche Menge. Eine Turingmaschine m bildet eine Folge von Zahlen '|', '||', ... solange, bis alle Elemente der Menge M abgearbeitet sind.
Satz: Die Menge aller Wörter A* über einem Alphabet A ist aufzählbar. Eine Turingmaschine m bildet eine Folge von Worten aus A nach der Länge und lexikographisch geordnet.
Satz: Jede aufzählbare Menge ist auch abzählbar
Wie erklären Sie den Ausdruck k |--*m k' ?
Definieren Sie eine kleine Turingmaschine und geben ein Beispiel für eine Ableitung.
Was unterscheidet totale von partiellen Funktionen. Finden sie Beispiele für beide Typen von Funktionen.
Was ist eine turingberechenbare Funktion? Geben Sie ein Beispiel an.
Was ist der Unterschied zwischen einem Entscheidungsverfahren und einem Semientscheidungsverfahren? Geben Sie jeweils ein Beispiel für ein Problem, das entscheidbar ist und ein solches, das nur semientscheidbar ist.
Was ist die charakteristische Funktion? Geben Sie ein Beispiel.
Was heisst es, dass eine Sprache L durch eine Turingmaschine entscheidbar ist?
Geben Sie das beispiel einer Sprache, die durch eine Turingmaschine nicht entscheidbar ist.
Was bedeutet es, dass eine Menge aufzählbar ist?
Ist die Menge aller Wörter A* über einem Alphabet A aufzählbar? Falls ja: warum, falls nein: warum nicht.