|
|
I-TI04 Theoretische Informatik WS04
|
In der vorausgehenden Vorlesung wurden informell anhand von konkreten Modellen drei Automatentypen eingeführt (Turingmaschine, Kellerautomat, Endlicher Automat). In dieser Vorlesung soll nun eine Formalisierung dier informellen Konzepte erarbeitet werden.
STARTIm Rahmen des Softwareengineerings [SWE] werden allgemeine Prozessmodelle vorgestellt, wie Informatiker Problemstellungen aus der realen Welt in formale Modelle übersetzen und diese dann implementieren. Die dort verwendeten formalen Modelle sind vielfach sehr spezielle Modelle, z.B. Modellierungen mit den Mitteln, die der UML-Standard bietet. An dieser Stelle werden wir den Vorgang der Formalisierung etwas grundssätzlicher betrachten.
Ausgangspunkt ist nochmals die Situation aus der letzten Vorlesung, in der skizzenhaft gezeigt wurde, wie ein bestimmter Wirklichkeitsausschnitt -im Bild schon idealisiert-- in das Modell eines Automaten übersetzt wird und dieses Modell dann weiter in einen realen Mikrocomputer (siehe Bild).
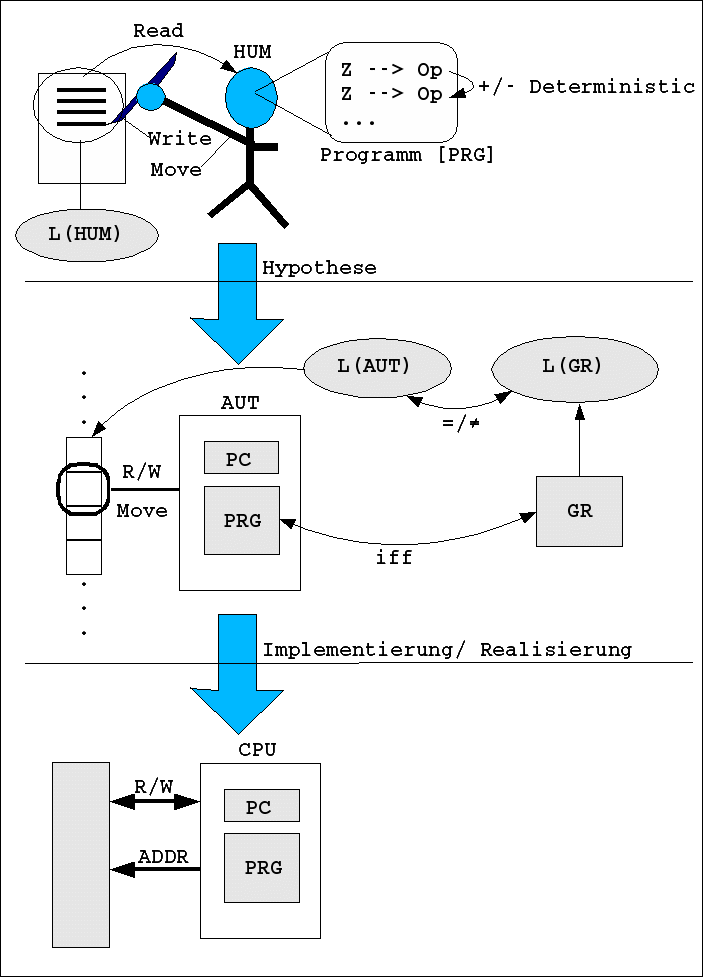
Realität -> Modell -> Maschine
Dieser Übersetzungsprozess sei hier nochmals explizit in den Rahmen der wissenschaftlichen Modellierung gestellt (siehe Schaubild):
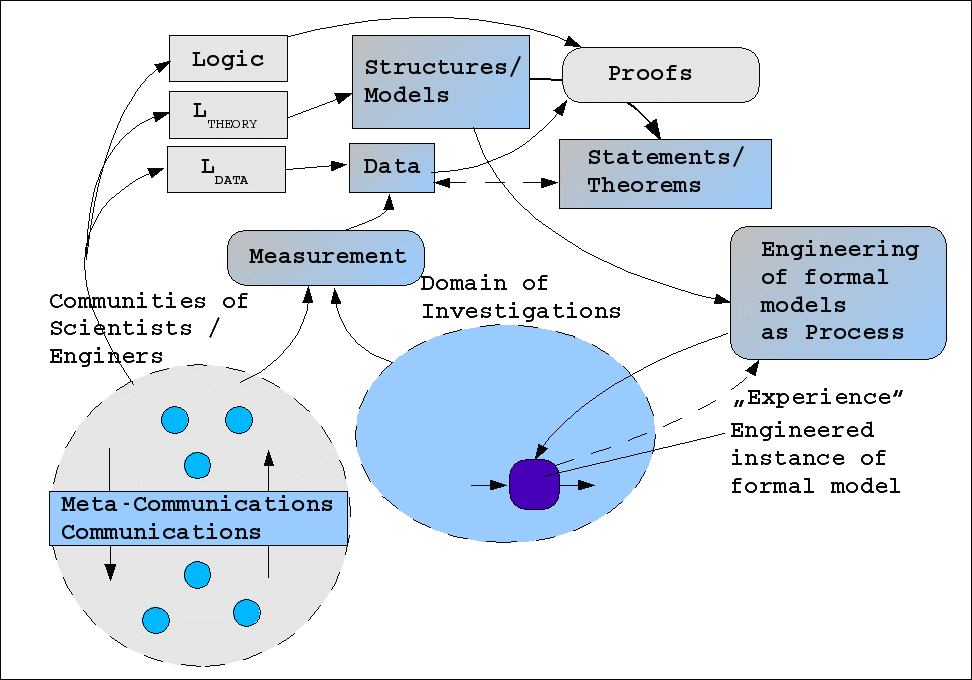
Formalisierung als Wissenschaft
In unserem Fall ist der Untersuchungsgegenstand ein Mensch, der eine Tätigkeit ausübt, die wir intuitiv als endlichen Prozess empfinden, d.h. von dem wir annehmen, dass er nach endlich vielen Schritten immer mit einem bestimmten Ergebnis endet.
Um diesen Gegenstand zu beschreiben, benötigen wir keine speziellen Messverfahren, nur unsere normale Beobachtung.
In einem ersten Schritt hatten wir ein graphisches Modell erstellt, das mit natürlicher Sprache kommentiert wurde.
In einem zweiten Schritt werden wir jetzt dieses graphische Modell in eine formale Darstellung übersetzen. Dazu werden wir die mengentheoretische Sprache benutzen. Als Zielformat für unsere formale Darstellung werden wir eine Strukturtheorie wählen, wie sie sich in der modernen Mathematik und Wissenschaftstheorie eingebürgert hat. Im Prinzip bildet man den darzustellenden Sachverhalt ab in Mengen von Objekten, Relationen über diesen Mengen sowie Axiome, die die Beziehungen der Mengen und Relationen untereinander weiter fixieren.
STARTIn der ersten Formalisierung soll eine deterministischen Turingmaschine (DTM) mit einem Band formalisiert werden.
Intuitiv besteht eine Turingmaschine aus einem nach beiden Seiten offenen Band ('tape'), das gleichmässig in rechteckige
Felder ('squares') unterteilt ist. Zu Beginn einer Rechnung ist das Band leer bis auf eine endliche Menge von Symbolen I aus
einem endlichen Alphabet A, die nacheinander auf das Band geschrieben sind, pro Feld ein Symbol. Alle anderen Felder
enthalten das leere Zeichen '§', das nicht zum Alphabet A gehört, also A cut {§} = 0 (In der Literatur gibt es eine Vielzahl von
Konventionen zur Bezeichnung des leeren Feldes {'b', 'B', 'kleines Epsilon', 'leeres Quadrat, 'Unterstrich mit Winkeln nach
oben', '*'}. Das Alphabet A ist nicht leer. Zu Beginn der Rechnung steht der Schreib-Lese-Kopf genau über dem ersten Feld
der Inschrift I. Die Turingmaschine befindet sich im Start-Zustand q0. Die Menge aller Zustände Q ist endlich. Neben dem Startzustand q0 enthält sie noch eine endliche Menge von Endzuständen E = {qe.1, ...,qe.k } mit k > 1. Die Aktionen einer DTM sind in der Maschinentafel, dem 'Programm' der Turingmaschine,
festgelegt. Eine Maschinentafel besteht aus einer endlichen nichtleeren Menge von Übergangsregeln P, wobei eine einzelne
Übergangsregel di die Form hat:
q: wenn der aktuelle Zustand q ist
a: und das Zeichen, das aktuell vom Schreib-Lesekopf gelesen wird, a ist,
b: dann soll auf das aktuelle Feld das Zeichen b geschrieben werden
m: der Schreib-Lesekopf soll dann in Richtung m bewegt werden.
q': und der nächste Zustand soll q' sein.
a,b sind aus G = A u {§} und
m ist aus {'L', 'R', 'S'}; es bedeutet 'L' := auf dem Band ein Feld nach 'links', 'R' := auf dem Band ein Feld nach
'rechts', 'S' := Stop, keine Bewegung mehr. Ein Zustand q als erstes Element einer Übergangsregel, bei dem als
Bewegung ein Stop-Symbol 'S' steht, heisst ein Stopzustand. Dieser sollte in der Maschinentafel von einem Endzustand gefolgt werden. Ein Enzustand it ein Zustand in der die Maschine stoppt unabhängig davon, welches Symbol gelesen wird und welche Richtung angegeben ist.
Beginnend mit dem Startzustand q0 auf dem ersten Zeichen einer Inschrift I wird eine DTM also einzelne Aktionen anhand der Menge der Übergangsregeln in der Maschinentafel ausführen. Grundsätzlich sind nun drei Fälle denkbar:
Eine DTM mit Argument I stoppt nach n-vielen Aktionen.
Eine DTM mit Argument I hat nach n-vielen Aktionen noch nicht gestoppt
Eine DTM mit Argument I gerät in eine Endlosschleife
Tritt Fall (1) ein, dann soll die Konvention gelten, dass die DTM die ursprüngliche Eingabe I gelöscht hat und der Schreib-Lesekopf am Ende auf dem ersten Zeichen des Ergebnisses steht; das Ergebnis kann leer sein.
Damit kann man nun folgende formalisierte Darstellung einer deterministischen Turingmaschine (DTM) geben:
DTM(m) gdw m = < < Q, A, G, {§}, {q0 }, E >, < P >>
mit
Q:= endliche nichtleere Menge von Zuständen
A:= endliches nichtleeres Alphabet
G = A u {§}; das endliche Bandalphabet
§ := das Leerzeichen
q0 := der Anfangszustand; q0 in Q
E := Menge der nichtleeren Endzustände; E C Q
M = {'L', 'R', 'S'}; endliche Menge von Richtungsaktionen ('links', 'rechts', 'stop')
P := endliche Menge von Übergangsfunktionen; das Programm, die Maschinentafel. Es gilt:
P C Q x G x G x M x Q und es gilt: P: Q x G ---> G x M x Q
k ist eine Konfiguration einer Turingmaschine m: CONFIGURATION(k,m) gdw m ist eine determinstische Turingmaschine & k ist eine Zeichenkette mit k = 'aqb' mit a,b aus G*m und q aus Qm. Auf dem Band befindet sich die Inschrift I = ab, eingerahmt von Blanks, und der Schreiblesekopf im Zustand q steht auf dem ersten Zeichen von b. Folgende Fälle sind hier zu unterscheiden:
q ist der Startzustand q0 und a ist leer; dies nennen wir eine Startkonfiguration ('START_CONFIGURATION') und b die Eingabe (bzw. den Input) der Turingmaschine;
q ist ein Endzustand qend und a ist wiederum leer (zum Ende steht immer nur das Ergebnis auf dem Band). Dies nennen wir eine Endkonfiguration ('END_CONFIGURATION') und b ist das Ergebnis (bzw. der Output) der Turingmaschine m;
q ist weder Start- noch Endzustand, d.h. q ist weder q0 noch qend.
Die Menge der Konfigurationen ('configurations') einer Turingmaschine m: configurations(m) = { k | CONFIGURATION(k,m) }
Der INPUT (bzw. die EINGABE) x einer Turingmaschine m: INPUT(x,m) gdw TM(m) & '§q0x' ist eine Startkonfiguration von m
Direkte Nachfolgekonfiguration einer Turingmaschine m: eine 'direkte Nachfolgekonfiguration' von aqb ist die Zeichenkette a'q'b', wenn a'q'b' aus aqb durch Anwendung einer Übergangsregel di entstanden ist. Man schreibt:
PROT ist ein Protokoll ('protocol') mit der Länge n von der Turingmaschine m für die Eingabe x : PROTOCOL(PROT,m,x,n) gdw PROT ist ein Tupel der Länge n & rn(PROT) C configurations(m) & (A:i)( i in dm(PROT) ==> ki |-- ki+1 mit i < n )
k' ist die Nachfolgekonfiguration von k bei einer Turingmaschine m oder k' ist ableitbar von k mit einer Turingmaschine m: ABL(k',k,m) gdw (E:PROT,n)( PROTOCOL(PROT,m,k,n) & END_CONFIGURATION(k',m) & k' = PROTn. Statt ABL(k',k,m)
schreibt man auch:
n ist die Länge ('length') einer Ableitung einer Turingmaschine m für die Eingabe k: k |--*m k' ==> lenth(k,k',m) = n gdw (E:P) PROTOCOL(P,m,k,n)
Rechenzeit: die Rechenzeit einer DTM ist die Zahl der Zustandsübergänge, bis die TM, angesetzt auf die Eingabe k mit dem Ergebnis k' stoppt. Da jeder endlichen Berechnung eine Ableitung korrespondiert, kann man auch sagen, die Rechenzeit entspricht der Länge der Ableitung von k' aus k unter m.
Die Eingabe x aus der Sprache L über dem Alphabet A ∪ {Y} wird von einer Turingmaschine m akzeptiert ('accepted'):
ACCEPT(x,L,A,m) gdw DTM(m) & x ∈ L & L C A* & (E:q',b)( §q0x |--*m §q'b & b = 'Y§' & q' in E)
/* Die Ausgabe von 'Y' für YES ist hilfreich, wenn man ein Entscheidungsverfahren bauen will */
Die von einer Turingmaschine m akzeptierte Sprache L über dem Alphabet A [L(A,m)]:
L(A,m) = { x | TM(m) & x ∈ L & ACCEPT(x,L,A,m) }
Die Eingabe x aus der Sprache L über dem Alphabet A ∪ {N} wird von einer Turingmaschine m verworfen ('rejected'):
REJECT(x,L,A,m) gdw DTM(m) & x ∉ L & L C A* & (E:q',b)( §q0x |--*m §q'b & b = 'N§' & q' in E)
/* Die Ausgabe von 'N' für NO ist hilfreich, wenn man ein Entscheidungsverfahren bauen will */
Die von einer Turingmaschine m verworfene Sprache L über dem Alphabet A [¬L(A,m)]:
¬L(A,m) = { x | TM(m) & x ∉ L & REJECT(x,L,A,m) }
L ist eine von einer Turingmaschine m entscheidbare Sprache L über dem Alphabet A [DEC(L,A,m)] gdw
¬L = A*\L & L = L(A,m) & ¬L = ¬L(A,m)
Sprache L über dem Alphabet A ist durch eine Turingmaschine m unentscheidbar [UNDEC(L,A,m)] gdw ¬DEC(L,A,m)
L ist eine von einer Turingmaschine m semientscheidbare Sprache L über dem Alphabet A [SDEC(L,A,m)] gdw
L = L(A,m)
Simulation: Ein Automat M' simuliert einen Automat M gdw für jedes Argument w mit M(w) = w' gilt M'(w) = w'. Damit ist vereinbar, dass der Platz- und/oder Zeitbedarf von M' grösser oder kleiner ist als von M.
Das Programm parity.tm als Eingabe für den Simulator von Christoph Jung. Dabei enthält die erste Zeile Metadaten, die nicht zum Programm gehören. Das Format dieser Datei ist <q,a,q',b,m>.
| parity.tm |
|---|
01_ 01 ab 0 E 000_R 011_R 0_E0S 101_R 110_R 1_E1S |
gerd@kant:~/public_html/fh/I-TI04/VL/VL3> ./turing parity.tm
Turingmaschinen-Simulator - (C) 1996 by DL9AAI (Andreas Jung)
=============================================================
Eingabealphabet: {01_}
Zustandsmenge : {01}
Bandalphabet : {ab }
Startzustand : 0
Endzustaende : {E}
Produktion 0: 00 |-> 0_R
Produktion 1: 01 |-> 1_R
Produktion 2: 0_ |-> E0S
Produktion 3: 10 |-> 1_R
Produktion 4: 11 |-> 0_R
Produktion 5: 1_ |-> E1S
(1) TM auf ein Wort ansetzen
(2) TM auf eine Konfiguration ansetzen
(3) L(T) aufzaehlen
(4) TM auf alle Woerter ansetzen
(0) Programm beenden
Ihre Wahl: 1
Wort ueber {01_ } eingeben: 01101_
================================================================|
01101_
0
========================== ENTER, Anzahl Schritte oder '.' =====>
_1101_
0
========================== ENTER, Anzahl Schritte oder '.' =====>
__101_
1
========================== ENTER, Anzahl Schritte oder '.' =====>
___01_
0
========================== ENTER, Anzahl Schritte oder '.' =====>
____1_
0
========================== ENTER, Anzahl Schritte oder '.' =====>
______
1
========================== ENTER, Anzahl Schritte oder '.' =====>
_____1
E
Turingmaschine akzeptiert.
================================================================|
(1) TM auf ein Wort ansetzen
(2) TM auf eine Konfiguration ansetzen
(3) L(T) aufzaehlen
(4) TM auf alle Woerter ansetzen
(0) Programm beenden
Ihre Wahl:
START Noch zu schreiben ....