|
|
I-THINF WS 0203 - Vorlesung mit Übung
|
Das Ziel der heutigen Vorlesung ist die Beweisführung, dass die Menge der regulären Sprachen LREG, die von regulären Grammatiken (Chomsky Hierarchie Typ3) definiert werden, identisch ist, mit der Menge der Sprachen LDFA, die von einem deterministischen endlichen Automaten DFA erkannt wird. Ferner wird gezeigt, dass die Sprachen LNFA, die von einem nichtdeterministischen Automaten NFA erkannt werden können, die gleichen sind, wie die Sprachen LDFA. Bevor diese Beweise geführt werden, werden zunächst Beispiele für alle beteiligten Begriffe gegeben.
Es wird jetzt das Beispiel einer regulären Grammatik g4 im Format einer rechtslinearen Grammatik gegeben, die die folgende Sprache definiert: L(g4,3) = {anne, anke, abzug, ablage}
FG(g4,3) mit g4 = < <Vg4,Tg4,Sg4 > Pg4>
mit
Vg4 = {S, X, Y, Z, G, H, M, V}
Tg4 = {a, b, e, g, k, l, n, u, z}
Pg4 = {(S,aX), (X,bY),(X,nZ),(Y,zV),(Y,lW),(V,uM),(W,aG),(G,gH),(Z,nG),(Z,kG),(M,g),(H,e)}
Vereinbarungsgemäss kann man statt (S,aX) auch schreiben S ---> aX und statt '(X,bY),(X,nZ)' kann man auch schreiben X --> bY | nZ.
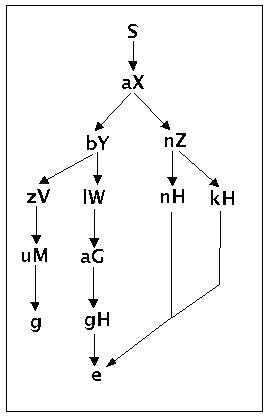
Syntaxbaum zur Grammatik g4
Laut Definition ist ein Wort w dann in der Sprache L(g4,3) wenn w in g4 ableitbar ist, also Sg4 *=>g4 w, und g4 ist eine formale Grammatik vom Typ3, also FG(g4,3). Man müsste also zeigen, dass die Worte {anne, anke, abzug, ablage} alle ableitbar sind und auch nur genau diese.
Eine Möglichkeit, dies zu tun besteht darin, dass man bezogen auf den Syntaxbaum ein allgemeines Verfahren (Algorithmus) definiert, das diesen Baum systematisch absucht. Ein Verfahren wäre das folgende (informelle Beschreibung):
Beginne bei dem Wurzelknoten S
Markiere letzten Knoten und gehe zum nächsten. Wenn es Alternativen gibt, wähle den am weitesten links liegenden Knoten.
Ist der Pfad zu Ende ohne ein terminales Element, dann Fehlermeldung
Andernfalls gebe den Pfad aus.
Backtracking: suche rückwärts den nächsten noch nicht markierten Pfad
Falls es keinen mehr gibt: Ende
Andernfalls setze fort bei 2
Wenn dieses Verfahren keine Fehlermeldung produziert, dann generiert es die Menge aller möglichen Pfade. Hier ein Beispiel für Ableitungen nach diesem Verfahren:
S (S ---> aX)
aX (X ---> bY)
abY (Y ---> zV)
abzV (V ---> uM)
abzuM (M ---> g)
abzug
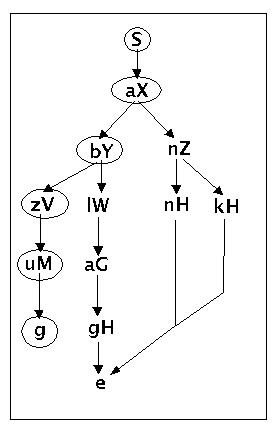
Syntaxbaum zur Grammatik g4 nach erster Ableitung
Ein Pfad im Syntaxbaum ist jetzt markiert. Mittels Backtracking wird jetzt rückwärts nach einer möglichen Fortsetzung gesucht. Diese ist hinter dem Knoten 'bY' gegeben. Es wird also hier eine zweite Ableitung versucht:
S (S ---> aX)
aX (X ---> bY)
abY (Y ---> lW)
ablW (W ---> aG)
ablaG (G ---> gH)
ablagH (H ---> e)
ablage
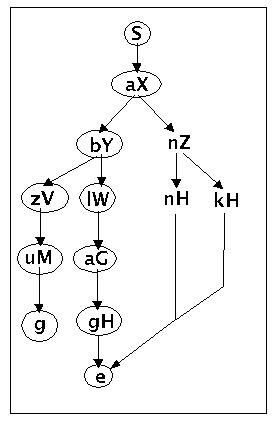
Syntaxbaum zur Grammatik g4 nach zweiter Ableitung
Entsprechend leitet man die beiden restlichen Worte 'anne' und 'anke' ab. Das Verfahren stoppt an dieser Stelle, da alle Knoten markiert sind. Auserdem wurde keine Fehlermeldung ausgegeben. Also wurden genau die Worte erzeugt, die die Sprache definieren. Damit wäre nun ein Beispiel für eine reguläre Grammatik und der durch sie definierten Sprache gegeben. Im nächsten Beispiel wird gezeigt, wie ein endlicher deterministischer Automat eine solche reguläre Sprache erkennen kann.
Man überzeuge sich an diesem Beispiel auch davon, dass die Verwendung einer linkslinearen statt einer rechtslinearen Form am Ergebnis nichts ändern würde.
Zunächst wird an einem konkreten Beispiel informell gezeigt, wie man, ausgehend von einer regulären Grammatik, einen deterministischen endlichen Automaten konstruieren kann, der genau diese Sprache erkennt. Anschliessend ird dies in allgemeiner Form bewiesen.
Den Ausgangspunkt für die Konstruktion eines konkreten deterministischen endlichen Automaten a4 auf der Basis der Grammatik g4 bilden die folgenden Annahmen:
Jede Regel (u,w) in Pg4 mit der Form A ---> a mit A in Vg4 & a in Tg4 wird übersetzt < A,a,q> in Pa4 mit q in Ea4
Jede Regel (u,w) in Pg4 mit der Form A ---> aB mit A,B in Vg4 & a in Tg4 wird übersetzt < A,a,B> in Pa4
Qa4 = Vg4
q0 = Sg4
Ea4 ist die Menge aller q in < A,a,q>, die aus A ---> a hervorgegangen sind. Es soll '1' den akzeptierenden Endzustand bezeichnen, also 1 in E
Mit diesen Annahmen kann man jetzt die Grammatik g4 direkt in einen Automaten a4 übersetzen, nämlich:
a4 = < <Qa4, Ta4, {q0}, Ea4 > Pa4> mit
<S,a,X>
<X,n,Z>
<X,b,Y>
<Y,lW>
<Y,z,V>
<W,a,G>
<G,g,H>
<H,e,1>
<V,u,M>
<M,e,1>
<Z,n,H>
<Z,k,H>
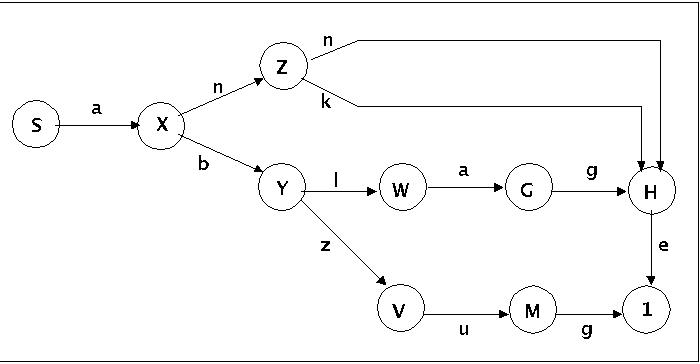
Zustandsgraph des DFA a4
Ob der Automat die Sprache L(g4,3) = {anne, anke, abzug, ablage} erkennt oder nicht, kann man informell am Zustandsgraphen überprüfen, indem man ein Wort x aus L(g4,3) nimmt, z.B. x = anne. Da es ausgehend von S eine Ereigniskette 'a', 'n', 'n' und 'e' entlang der Zustände S, X, Z,H gibt, die im Endzustand E endet, gilt, dass der Automat das Wort x=anne erkennt.
Mithilfe des Ableitungsbegriffs von a4 kann man dies auch ganz formal durchspielen. Wegen
x in T(a4) gdw x in {w | w in Ta4* & Pa4'(q0,w) in Ea4 }
gilt also, das x=anne genau dann ein Wort von T(a4) ist, wenn w ein Wort über dem terminalen Alphabet Ta4 von a4 ist und die Anwendung von Pa4' auf w einen Zustand ergibt, der ein Endzustand ist. Konkret, da q0 = S, gilt (für die Definition von P'() siehe VL8):
P'(S,anne)
P'(P(S,a),nne)
P'(X,nne)
P'(P(X,n),ne)
P'(Z,ne)
P'(P(Z,n)e)
P'(H,e)
P'(P(H,e),§)
P'(1,§)
1
Man sieht, dass es eine Ableitung gibt, die im Zustand 1 endet, wobei 1 ein Endzustand ist. Statt dies jetzt für alle Einzelfälle durchzuspielen, beweisen wir jetzt einen allgemeinen Satz.
Wir wollen jetzt ganz allgemein beweisen, dass jede reguläre Sprache durch einen deterministischen Automaten erkannt wird. Formal sieht der Satz folgendermassen aus:
(A:l,g)( l = L(g,3) ==> (E:a)( DFA(a) & l = T(a) ))
Für alle l, die einer durch eine formale Grammatik g vom Typ 3 ableitbare Sprache entsprechen, gibt es einen deterministischen endlichen Automaten a und l entspricht der durch a erkennbaren Sprache T(a).
Angenommen also, wir haben ein l = L(g,3)
Dann gilt, dass ein x in l gdw wenn x in L(g,3)
Dann gilt, dass ein x in L(g,3) gdw ABL(x,Sg,g) & FG(g,3)
Dann gibt es ein g = < <Vg,Tg,Sg > Pg>
Ausgehend von g kann man dann ein a' definieren, das die folgenden Eigenschaften hat:
a' = < <Qa', Ta', {q0}, Ea' > Pa'> mit
Qa' = Vg
Ta' = Tg
q0 = Sg
Pa' wird aus Pg dadurch gebildet, dass man für alle (u,w) in Pg setzt:
wenn w = a (a in Tg), dann < u,w,e> in Pa' mit e in Ea'
wenn w = aB (a in Tg, B in Vg), dann < u,w,B> in Pa'
Aus ABL(x,Sg,g) folgt, dass es eine endliche Ableitung der folgenden Art gibt, wobei wir annehmen x=a1a2...an-1an
Sg
a1V1
a1a2V2
...
a1a2...an-1Vn-1
a1a2...an-1an
Dies bedeutet, ausgehend vom Startsymbol Sg wird durch Anwendung von Regeln aus g eine endliche Ableitung erzeugt, an deren Ende die Zeichenkette x steht.
Aus a' folgt, dass man zu jeder solchen Ableitung auch eine Ableitung mittels Pa' sowie mittels Pa'' erzeugen kann. Sei x=a1a2...an-1an wie oben, dann gilt:
P'(q0,a1a2...an-1an)
P'(P(q0,a1),a2...an-1an)
P'(q1,a2...an-1an)
P'(P(q1,a2),...an-1an)
P'(q2,a3...an-1an)
...
P'(P(qn-1,an),§)
P'(qn,§)
qn
Da jede Regel von Pg nach Pa' abgebildet wurde, gibt es, beginnend mit q0, Regeln, die sich auf q0 und dann auf die Folgezustände anwenden lassen. Denn, entweder handelt es sich um eine Regel aus A ---> aB, dann führt P(A,a) in den Folgezustand B, oder aber es handelt sich um eine Regel aus A ---> a, dann gilt, dass P(A,a) auf einen Folgezustand e führt, der aus den Endzuständen Ea' stammt. Der Fall P'(qn-1,an) beschreibt genau dieses, denn hinter an kommt kein weiteres Zeichen; dies entspriicht der Regel Vn-1 ---> an, d.h. P'(P(qn-1,an),§) erzeugt einen Folgezustand qn, der zu Ea' gehört,
also wurde die Eingabe x erkannt, .
d.h. w in L(g,3) ==> x in T(a')
Da man jede Ableitung, die zu T(a') führt, auch in eine Ableitung umformen kann, die zu L(g,3) führt, folgt weiter:
x in T(a') ==> x in L(g,3)
also L(g,3) = T(a')
also l = T(a')
also (E:a)( DFA(a) & l = T(a) )
also l= L(g,3) ==> (E:a)( DFA(a) & l = T(a) )
also (A:l,g)( l= L(g,3) ==> (E:a)( DFA(a) & l = T(a) ))
Wie man aus dem vorausgehenden Beweis sieht, kann man auch noch einen viel kompakteren Satz beweisen, nämlich dass jede durch eine formale Grammatik g vom Typ3 erzeugbare Sprache eine Teilmenge der Sprachen ist, die von einem deterministischen Automaten a erkannt werden. Ausführlich:
(A:g,a)( L(g,3) C T(a) )
Anders geschrieben: (A:x)( x in L(g',3) ==> x in T(a') )
Angenommen also: x' in L(g',3)
Dann: x' in L(g',3) gdw ABL(x',Sg,g) & FG(g',3)
Analog zum vorausgehenden Beweis kann man dann aufgrund der Existenz einer formalen Grammatik g' einen deterministischen endlichen Automaten a' definieren.
Aus der Existenz von a' ergibt sich dann eine Ableitung mit P'a für x'
also x' in T(a')
dann x' in L(g',3) ==> x' in T(a')
dann (A:x)( x in L(g',3) ==> x in T(a') )
dann L(g',3) C T(a')
dann (A:g,a)( L(g,3) C T(a) )
Jetzt sollte auch schon klar sein, wie man die Umkehrung des vorausgehenden Satzes beweisen kann, nämlich dass jede von einem deterministischen Automaten a erkannte Sprache auch eine reguläre Sprache ist, formal:
(A:a,g)( T(a)C L(g,3))
Anders geschrieben: (A:x)( x in T(a') ==> x in L(g',3) )
Angenommen also: x' in T(a')
Dann: x' in Ta'* & DFA(a') & P'a'(q0,x') in Ea'
Auf der Basis von DFA(a') kann man dann eine formale Grammatik g' definieren.
Aus der Existenz von g' folgt dann die Existenz einer Ableitung ABL(x',Sg',g')
Also: x' in L(g',3)
Also: x' in T(a') ==> x' in L(g',3)
Also: (A:x)( x in T(a') ==> x in L(g',3) )
Also: T(a')C L(g',3)
Also: (A:a,g)( T(a)C L(g,3) )
Aus den beiden vorausgehenden Sätzen ergibt sich jetzt der Satz, dass die Menge der durch einen deterministischen Automaten erkennbaren sprachen identisch ist mit der Menge der durch eine reguläre Grammatik erzeugbarenb Sprachen, 'direkt':
(A:a,g)( T(a)= L(g,3) )
Es wird jetzt das Beispiel einer regulären Grammatik g5 im Format einer rechtslinearen Grammatik gegeben, die die gleiche Sprache wie die Grammatik g4 definiert: L(g5,3) = {anne, anke, abzug, ablage}. Trotzdem unterscheidet sich die Grammatik g5 von der Grammatik g4 durch die benutzten Regeln:
FG(g5,3) mit g5 = < <Vg5,Tg5,Sg5 > Pg5>
mit
Vg5 = {S, X1, X2, Y1, Y2, Z1, Z2, G, H, M, V}
Tg5 = {a, b, e, g, k, l, n, u, z}
Pg5 = {(S,aX1),(S,aX2),(X1,bY1),(X1,bY2),(X2,nZ1 ),(X2,nZ2), (Ysub>1,zV),(Y2,lW),(V,uM), (W,aG),(G,gH),(Z1,nG),(Z2,kG),(M,g),(H,e)}
Man sieht, dass durch die Änderung der Produktionsregeln von g5 zusätzliche Alternativen entstehen.
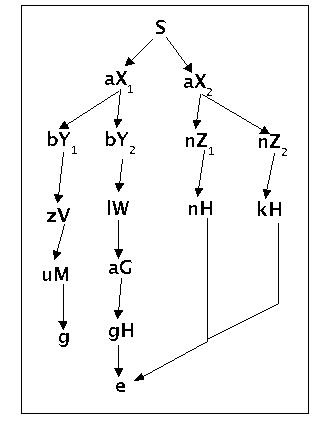
Syntaxbaum zur Grammatik g5
Für die Ableitung (bzw. Erzeugung) von Worten mit der Grammatik g5 gelten die gleichen Regeln wie oben im Fall der Grammatik g4. Das Hauptaugenmerk liegt in diesem Fall darauf, aus der Grammatik g5 einen nichtdeterministischen endlichen Automaten a5 zu konstruieren.
Jede Regel (u,w) in Pg5 mit der Form A ---> a mit A in Vg5 & a in Tg5 wird übersetzt < A,a,{q}> in Pa5 mit q in Ea5
Jede Regel (u,w) in Pg4 mit der Form A ---> aB1 | ... | aBn mit A,Bi in Vg5 & a in Tg5 wird übersetzt < A,a,{B1, ..., Bn}> in Pa5
Qa5 = Vg5
Sa5 = Sg5 /* a5 hat eine Menge von Anfangszuständen ! */
Ea5 ist die Menge aller q in < A,a,{q}>, die aus A ---> a hervorgegangen sind. Es soll '1' den akzeptierenden Endzustand bezeichnen, also 1 in E
Mit diesen Annahmen kann man jetzt die Grammatik g5 direkt in einen Automaten a5 übersetzen, nämlich:
a5 = < <Qa5, Ta5, Sa5, Ea5 > Pa5> mit
Pa5 = {
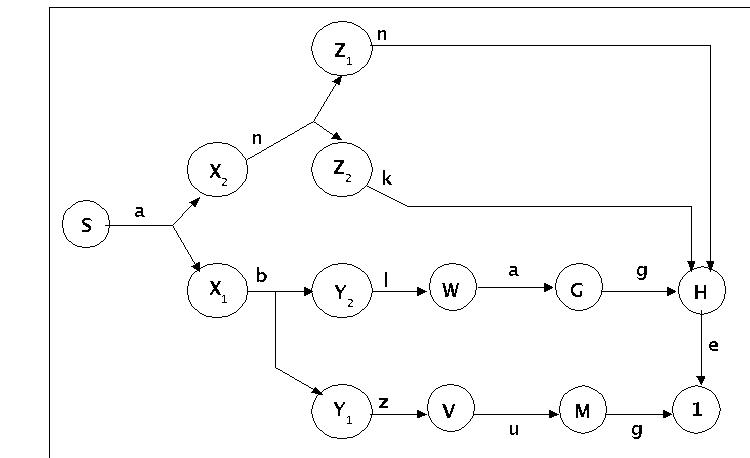
Zustandsgraph zum NFA a5 auf Basis der Grammatik g5
Ob der Automat die Sprache L(g5,3) = {anne, anke, abzug, ablage} erkennt oder nicht, kann, analog wie im obigen Beispiel mit dem endlichen Automaten a4, wieder informell am Zustandsgraphen überprüfen, indem man ein Wort x aus L(g5,3) nimmt, z.B. x = anne. Da es ausgehend von S eine Ereigniskette 'a', 'n', 'n' und 'e' entlang der Zustände S, X2, Z1,H gibt, die im Endzustand 1 endet, gilt, dass der Automat das Wort x=anne erkennt.
Mithilfe des Ableitungsbegriffs von a5 kann man dies auch ganz formal durchspielen. Wegen
x in T(a5) gdw x in {w | w in Ta5* & Pa5'(Sa5,w) cut Ea5 != 0 }
gilt also, das x=anne genau dann ein Wort von T(a5) ist, wenn w ein Wort über dem terminalen Alphabet Ta5 von a5 ist und die Anwendung von Pa5' auf w eine Menge von Zuständen ergibt, von denen mindestens einer ein Endzustand ist. Konkret, da Sa5 = S, gilt (für die Definition von P'() siehe VL8):
P'({S},anne)
P'({P(S,a)},nne)
P'({X1,X2 },nne)
P'({P(X1,n), P(X2,n) },ne)
P'({Z1, Z2 },ne)
P'({P(Z1,n), P(Z2,n) },e)
P'({H},e)
P'({P(H,e)},§)
P'({1},§)
1
1 in Ea5
Man sieht, dass es eine Ableitung gibt, die in einem Zustand 1 endet, wobei 1 ein Endzustand ist. .
Werden in der Übung gegeben.