|
|
I-THINF WS 0203 - Vorlesung mit Übung
|
Die bisherigen Vorlesungen haben im Prinzip zwei Konzepte eingeführt: einerseits das Konzept des Automaten (am Beispiel der Turingmaschine und des endlichen Automaten) sowie das Konzept der formalen Grammatik FG(g) und der durch eine formale Grammatik bestimmten Sprache L(g).
Wie es schon in der letzten Vorlesung anklang, kommt es zu einer 'Interaktion' zwischen Automat und Grammatik dort, wo es darum geht, zu erkennen, ob eine bestimmte Zeichenkette w Element einer Sprache L(g) ist, d.h. dass w ein Wort über dem terminalen Alphabet T* von g ist und dasss w aus dem Startsymbol von g ableitbar ist (SG |*--g w).
Im allgemeinen Fall geht es also darum, ob es einen Automaten gibt, der als Input eine Zeichenkette w bekommt und der in der Lage sein muss, zu entscheiden, ob w in L(g).
Aufgrund der vorausgehenden allgemeinen Ergebnisse wissen wir, dass nur Spachen von Typ 1-3 der Chomsky-Hierarchie entscheidbar sind. Wir werden von daher unsere Untersuchungen auf diese Sprachen beschränken. Konkret werden wir mit den 'schwächsten' Sprachen beginnen, den sogenannten rekursiven Sprachen, also jenen, die durch Typ3-Grammatiken definiert werden.
Die nächste Aufgabenstellung besteht daher darin, zu zeigen, welche Automaten man benötigt, um die regulären Sprachen (LREG) zu erkennen. Man weiss mittlerweile, dass es die deterministischen endlichen Automaten ('deterministic finite automata' (DFA)) sind, die hinreichen, um jede reguläre Sprache zu erkennen, d.h. die durch DFAs erkennbare Sprachen (LDFA) sind identisch mit den regulären Sprache LREG, die durch reguläre Grammatiken FG(g,3) definiert werden. Ferner konnte man mittlerweile zeigen, dass auch die nichtdeterministischen endlichen Automaten ('non-deterministic finite automata (NFA)) nur genau die regulären Sprachen erkennen, d.h. die durch NFAs erkannten Sprachen (LNFA) sind identisch mit den LDFAs.
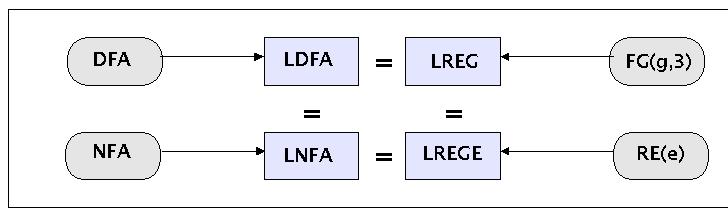
Beweisplan
Es wurden bis heute noch zahlreiche andere Ergebnisse bewiesen; wir beschränken uns auf diese zentralen Resultate. Ferner werden wir versuchen, zu verstehen, wie man, ausgehend von einer regulären Sprache L, den dazu passenden endlichen Automaten a bauen kann, um die Sprache L zu erkennen.
Leider, wie so oft, ist der Begriff des endlichen Automaten nicht so eindeutig, wie man es gerne hätte. Abhängig von unterschiedlichen Problemlösungskontexten wurden unterschiedliche Varianten von endlichen Automaten definiert. Daher soll hier zu Beginn ein kurzer Überblick über die wichtigsten Spielarten endlicher Automaten gegeben werden, bevor die Thematik in Richtung Erkennbarkeit von regulären Sprachen weiter entwickelt wird (siehe zu solch einem Überblick den Artikel von [YU 1997]).
Wir werden den Überblick so aufbauen, dass wir die Definition eines endlichen automaten aus den vorausgehenden Vorlesungen als Ausgangspunkt nehmen, und alle anderen Definitionen darauf beziehen. Auf diese Weise bekommt man eine ganz gute 'Taxonomie' aufgrund struktureller Vereinfachungen bzw. Verkomplizierungen.
Wir bezeichnen den von uns eingeführten endlichen Automaten in diesem Zusammenhang einfach mal als den Prototypen einer endlichen Maschine ('finite state machine' (FSM)), die dadurch gewonnen wurde, dass man aus der Definition der deterministischen Turingmaschine die Bewegung entfernte.
FSM(t) gdw t = < < Q, E, Ti, To, {§}, {q0 } >, < P > >
mit
Q:= endliche nichtleere Menge von Zuständen
E := Menge der Endzustände; E C Q & E != 0
Ti:= endliches Eingabe-Alphabet; |Ti| > 0
To:= endliches Ausgabe-Alphabet; kann leer sein
B = Ti u {§}; das endliche Bandalphabet
§ := das leere Zeichen
q0 := der Anfangszustand; q0 in Q
P ist das Programm des endlichen Automaten t und es gilt
P: (Q -E) x B --->
Q x To
MEALY(t) hat die Programmfunktion PMEALY: Q x B ---> Q x To ([YU 1997:66])
MOORE(t) hat die Programmfunktion PMOORE: Q x B --->
Q x To mit der Zerlegung PMOORE = FMOORE u GMOORE der Art:
FMOORE: Q x B ---> Q
GMOORE: Q ---> To
GENERALIZED_SEQUENTIAL_MACHINE(t) hat die Programmfunktion PGSM: Q x B ---> Q x To* ([YU 1997:67])
FINITE_TRANSDUCER(t) hat die Programmfunktion PFT: Q x Ti* ---> Q x To* ([YU 1997:67])
NON-DETERMINISTIC_FINITE_AUTOMATON(t) hat die Programmfunktion PNFA: Q x B ---> 2Q ([YU 1997:49ff])
DETERMINISTIC_FINITE_AUTOMATON(t) hat die Programmfunktion PDFA: Q x B ---> Q ([YU 1997:45ff])
ALTERNATING_FINITE_AUTOMATON(t) hat die Programmfunktion PAFA: Ti x BQ ---> B, wobei B ein 2-elementige Algebra ist mit <{0,1}, +, &, ¬,0,1 > ([YU 1997:54ff])
In dieser Aufstellung sieht man sofort die strukturelle Ähnlichkeit all dieser endlichen Automaten, aber auch die jeweiligen minimalen Abweichungen. Auf den ersten Blick sehr unterschiedlichen sind die alternierenden Automaten (AFAs); für eine effiziente Implementierung von endlichen Automaten erscheinen sie sehr interessant; vorläufig werden wir aber nicht auf dies Thema eingehen.
Für die weiteren Überlegungen beschränken wir uns zunächst auf die Varianten DFA und NFA. Beide Varianten endlicher Automaten erzeugen keinen expliziten Output. Sie werden nur, gesteuert durch die jeweilige Eingabe, durch unterschiedliche Folgen von Zuständen 'getrieben', die, im Erfolgsfall, in sogenannte Endzustände münden.
Um die Menge LDFA jener Sprachen definieren zu können, die durch einen DFA erkannt werden können, benötigen wir zusätzlich ein Konzept der Erkennbarkeit eines Inputwortes w durch einen deterministischen Automaten a (siehe zum Folgenden [SCHÖNING 2001:27ff]).
DFA(a) gdw a = < < Q, E, Ti, {q0 } >, P >
mit
Q:= endliche nichtleere Menge von Zuständen
E := Menge der Endzustände; E C Q & E != 0
Ti:= endliches Eingabe-Alphabet; |Ti| > 0
B = Ti u {§}; das endliche Bandalphabet
q0 := der Anfangszustand; q0 in Q
P ist das Programm des endlichen Automaten a und es gilt
P: Q x B --->
Q
Seien (q,z) in Q x B, dann gilt P(q,z) = q' mit q' als dem eindeutigen Nachfolgerzustand von q bei z.
Zusätzlich wird folgende Funktion P' definiert mit P': Q x Ti* ---> Q
P'(q,§) = q
P'(q,ax) = P'(P(q,a),x) (mit a in T und x in T*)
Mit Hilfe der Funktionen P' und P kann man nun jede Eingabe w entweder zu einem Zustand zurückverfolgen, der in E ist oder nicht. Damit kann man definieren:
(A:a)(T(a) = { x | x in T* & DFA(a) & P'a(q0,x) in Ea })
T(a) bezeichnet also die Menge der Ausdrücke, die der deterministische Automat a erkennen kann. Dann kann man weiter eine Konstante LDFA definieren:
LDFA = { L | (A:a)( L = T(a) )}
Analog zum DFA müssen wir nun, um die Menge LNFA jener Sprachen definieren zu können, die durch einen NFA erkannt werden können, zusätzlich ein Konzept der Erkennbarkeit eines Inputwortes w durch einen nicht-deterministischen Automaten a einführen (siehe zum Folgenden [SCHÖNING 2001:30ff]).
NFA(a) gdw a = < < Q, E, Ti, S >, P >
mit
Q:= endliche nichtleere Menge von Zuständen
E := Menge der Endzustände; E C Q & E != 0
Ti:= endliches Eingabe-Alphabet; |Ti| > 0
B = Ti u {§}; das endliche Bandalphabet
S := Menge von Anfangszuständen; S C Q
P ist das Programm des endlichen Automaten a und es gilt
P: Q x B --->
2Q
Seien (q,z) in Q x Ti, dann gilt P(q,z) = Q' mit Q' als Menge von Nachfolgerzuständen von q bei z.
Zusätzlich wird folgende Funktion P' definiert mit P': 2Q x Ti* ---> 2Q
P'(Q',§) = Q' (mit Q' C Q)
P'(Q',ax) = U(q in Q')( P'(P(q,a),x) ) (mit a in T und x in T*)
Mit Hilfe der Funktionen P' und P kann man nun jede Eingabe w entweder zu einer Menge von Zuständen Q' zurückverfolgen, von denen wenigstens einer in E ist oder nicht. Damit kann man definieren:
(A:a)(TN(a) = { x | x in T* & NFA(a) & P'a(S,x) cut Ea != 0)})
TN(a) bezeichnet also die Menge der Ausdrücke, die der nicht-deterministische Automat a erkennen kann. Dann kann man weiter eine Konstante LNFA definieren:
LNFA = { L | (A:a)( L = TN(a) )}
Werden in der Übung gegeben.