|
|
I-THINF WS 0203 - Vorlesung mit Übung
|
Im Anschluss an die grundlegenden Begriffe Abzählbarkeit, (rekursive) Aufzählbarkeit sowie Entscheidbarkeit (bzw. Rekursivität) wurde in der letzten Vorlesung der Begriff der formalen Grammtik eingeführt. Dieser Begriff muss nun noch durch einige grundlegende Begriffe wie Ableitbarkeit und der durch die Grammatik G definierten Sprache L(G) ergänzt werden. Dann kann man die Chomsky Hierarchie definieren. Ausgehend von der Chomsky Hierarchie werden dann konkrete Untersuchungen zu den einzelnen Sprachtypen 'reguläre Sprachen' sowie 'kontextfreie Sprachen' mitsamt den zugehörigen Automatentypen 'endlicher Automat' sowie 'Kellerautomat' angestellt.
Betrachten wir das Beispiel einer einfachen formalen Grammatik g1. Es soll gelten:
FG(g1) und g1 = < <Vg1,Tg1,{Sg1} >, Pg1> mit den Werten:
Vg1 = {E,T,F},
Tg1 = {(,),a,+,*},
Sg1 = E
Pg1 = {(E,T), (E,E + T), (T,F),(T,T * F),(F,a),(F,(E))}
Statt (E,T) kann man vereinbarungsgemäss auch schreiben E --> T, und entsprechend für die anderen Regeln.
Man muss jetzt festlegen, was es heisst, dass man mit den Produktions-Regeln einer formalen Grammatik ein zulässiges Wort der Grammatik erzeugt bzw. ableitet.
y ist in g direkt ableitbar aus x; DABL(y,x,g) [x =>g y bzw. x |-g y] gdw
(E:a,b,k,k')( (a,b) in Pg & x = kak' & y = kbk' & k,k',b in (Vg u Tg)* )
y ist in g ableitbar aus x; ABL(y,x,g) [x *=>g y bzw. x |*-g y]
gdw
(E:f)( SEQ(f) & (f:Nat ---> (Vg u Tg)* & A:i,j)( i,j in dm(f) & j =i+1 =>
DABL(fj,fi,g) & x = f0 & y =flen(f)-1 ))
'SEQ(f)' heisst, dass f eine Folge ist (siehe mengentheoretische
Grundbegriffe) und x ist das erste Element der Folge und y ist das letzte Element der Folge. Da der Index einer Folge mit Nat
ab 0 läuft, hat das letzte Element einer Folge f den Index len(f)-1 = |dom(f)|-1.
L ist die durch g erzeugbare Sprache [L(g)] = { w | FG(g) & ABL(w,Sg,g) }
Die durch die Grammatik g bestimmte Sprache besteht also aus allen Worten w, die sich aus dem Startelement Sg der
Grammatik g ableiten lassen.
Grammatik g ist äquivalent zu Grammtik g' AEQUIVALENT(g,g')] gdw FG(g) & FG(g') & L(g) = L(g')
Beispiele von Ableitungen mit der vorausgehenden Beispielsgrammatik wären die folgenden:
Satz: E *=>g1 a
Beweis:
E (Startsymbol)
T (mit E --> T)
F (mit T --> F)
a (mit F --> a)
Satz: E *=>g1 a * a + a
Beweis:
E (Startsymbol)
E + T (mit E --> E+T)
T + T (mit E --> T)
T*F + T (mit T --> T*F)
F*F + F (mit T --> T 2x anwenden)
a*a + a (mit F --> a 3x anwenden)
Anhand der Definition von Bäumen kann man eine direkte Zuordnung herstellen zwischen formalen Grammatiken einerseits und Bäumen andererseits. Dies kann man in einem Algorithmus fassen:
Gegeben ist eine formale Grammatik g mit < <Vg,Tg,{Sg} >, Pg>
Gesucht ist ein gerichteter Graph g' mit < <Eg', {rg'} >, Kg'>< < mit den Werten Eg' = Vg u Tg und rg' = Sg . Dies bedeutet, die Variablen Vg und terminalen Symbole Tg von g werden in die Menge der Ecken Eg' von g' abgebildet; dabei wird das Startsymbol Sg mit dem Wurzelknoten rg' von g' identifiziert. Schliesslich werden die Produktionsregeln Pg in die Menge der Kanten Kg' abgebildet.
Man kann dann auf der Basis der Kanten Kg' dadurch einen Baum konstruieren, dass man, beginnend mit dem Wurzelknoten rg', alle Nachfolger der Wurzel über Pfeile mit der Wurzel verbindet, dann alle Nachfolger der Nachfolger usw.
Wie sich gezeigt hat, ist die oben eingeführte Definition einer formalen Grammatik in ihrer Allgemeinheit so stark, dass sie für solche Anwendungen, in denen in endlichen Zeitintervallen Entscheidungen getroffen werden müssen, solche Entscheidungen entweder garnicht möglich sind oder aber nur mit einem unakzeptablen Zeitaufwand. Dies hat dazu geführt, dass man auch schwächere Formen von formalen Grammatiken untersucht hat, also solche Grammatiken, deren Sprachen sich mittels Automaten in vertretbaren Zeiten 'erkennen' lassen.
Die Formulierung vertretbarer Zeitaufwand ist in diesem Zusammenhang mehrfach ambivalent:
Anwendungskontext: bei klassischer Briefpost erwartet man Antworten in Zeiträumen von einigen Tagen; bei email möglicherweise in Stunden oder Minuten; beim Bremsen im Auto erwartet man 'sofort' eine Reaktion usw.
Hardware: je nach verfügbarer Hardware kann der gleiche Berechnungsprozess Stunden, Minuten oder Sekunden dauern oder gar noch weniger Zeit beanspruchen.
Rekursiv/ Entscheidbar: das Problem ist grundsätzlich entscheidbar, auch wenn es, wie im Fall der Typ-2-Sprachen (s.u.) möglicherweise in der Praxis nicht nutzbar ist.
Im vorliegenden Kontext ist der Fall der entscheidbaren Sprachen von grösstem Interesse. Die folgende auf Noam CHOMSKY zurückgehende Klassifizierung hat sich eingebürgert:
g ist eine formale Grammatik vom Typ 0 [FG(g,0)] (Phrasenstrukturgrammatik, 'Phrase Structure Grammar' [PSG]) gdw FG(g)
g ist eine formale Grammatik vom Typ 1 [FG(g,1)](Kontextsensitive Grammatik, 'Contextsensitive Grammar' [CSG]) gdw
FG(g) & (A:u,w)( (u,w) in Pg =>
(E:a,b,X,p)([u = aXb & w = apb & X in Vg &
( [a,b in (Vg u Tg)* & p
in ( Vg u Tg)+ ] + [ a,b in ((Vg
u Tg) - {Sg})* & p in (Vg u Tg -
{Sg})*] ))
Der entscheidende Punkt ist, dass die Ersetzung von X durch p nur bei Vorliegen des
Kontextes 'a_b' erlaubt ist. Ferner darf p nicht leer sein; Falls man p=§ zulässt, dann darf das Startsymbol S nicht
mehr auf der rechten Seite einer Produktion auftreten.
g ist eine formale Grammatik vom Typ 2 [FG(g,2)](Kontextfreie Grammatik, 'Contextfree Grammar' [CFG]) gdw
FG(g) & (A:u,w)( (u,w) in Pg => u in Vg )
g ist eine formale Grammatik vom Typ 3 [FG(g,3)](Reguläre Grammatik, 'Regular Grammar')gdw
FG(g,2) & RECHTSLINEAR(g) + LINKSLINEAR(g))
g ist eine rechtslineare formale Grammatik vom Typ 3 [RLFG(g,3)] gdw
FG(g,3) & (A:u,w)( (u,w) in Pg =>
(E:a,B)(B in Vg & a in Tg & [w=a + w=aB] ))
g ist eine linkslineare formale Grammatik vom Typ 3 [LLFG(g,3)] gdw
FG(g,3) & (A:u,w)( (u,w) in Pg =>
(E:a,B)(B in Vg & a in Tg & [w=a + w=Ba] ))
L ist die durch eine formale Grammatik vom Typ i erzeugte Sprache [L(g,i)] gdw
Satz: L(g,3) C L(g,2) C L(g,1) C L(g,0)
Ein Beispiel für eine kontextsensitive Grammatik ist die Grammatik g2:
FG(g2,1) und g2 = < <Vg2,Tg2,{Sg2} >, Pg2> mit den Werten:
Vg2 = {S,B,C},
Tg2 = {a,b,c},
Sg2 = S
Pg2 = {(S,aSBC), (S,aBC), (CB,BC),(aB,ab),(bB,bb),(bC,bc), (cC,cc)}
Ein Beispiel für eine kontextfreie Grammatik war die vorausgehende Grammatik g1.
Zwei Beispiele für reguläre Grammatiken sind die Grammatiken g3 und g4
FG(g3,3) und g3 = < <Vg3,Tg3,{Sg3} >, Pg3> mit den Werten:
Vg3 = {S},
Tg2 = {0},
Sg2 = S
Pg2 = {(S,0S), (S,0) }
FG(g4,3) und g4 = < <Vg4,Tg4,{Sg4} >, Pg4> mit den Werten:
Vg4 = {S},
Tg4 = {0,1},
Sg4 = S
Pg4 = {(S,0), (S,1), (S,0S), (S,1S) }
Um zu entscheiden, ob ein Wort w zu einer durch die Grammtik g bestimmten Sprache L(g) gehört, benutzt man sehr oft Automaten, die auf die jeweilige Grammtik abgestimmt sind. Insofern es sich bei allen Automaten letztlich immer entweder um die Turingmaschine oder abgeschwächten Formen von dieser handelt, kann man immer davon ausgehen, dass Bänder vorliegen, auf denen das zu entscheidende Wort als Eingabewort steht. Der zur Grammatik g passende Automatg berechnet dann in endliche vielen Schritten, ob das Wort zur Sprache L(g) gehört oder nicht.
Eine erste konkrete Untersuchung soll nun dem Zusammenspiel von endlichen Automaten und regulären Sprachen dienen.Wie sich später zeigen wird, kann man beweisen, dass man mit endlichen Automaten genau die regulären Sprache erkennen und umgekehrt kann man mit den regulären Sprachen nur solche Probleme formulieren, die von endlichen Autoamten erkannt werden klönnen.
Wie aus der VL Rechnerarchitektur schon bekannt, ist ein endlicher Automat (engl. 'finite state automaton (FSA)' oder 'finite state machine (FSM)'), der sich von einer Turingmaschine nur dadurch unterscheidet, dass er keine Möglichkeit hat, das Verhalten des Lese-Schreib-Kopfes selbständig zu beeinflussen. Im Prinzip kann man sich das Verhalten eines endlichen Automaten so vorstellen (siehe Bild), dass das Band in zwei Hälften geteilt ist: irgendwo steht eine Inschrift, die den Input für den Automaten bildet und der Lesekopf steht auf dem ersten Feld des Inputs; auf dem ersten Feld rechts von dem Input steht der Schreibkopf. Der Lesekopf kann sich bei jeder Aktion ein Feld nach links bewegen und der Schreibkopf ein Feld nach rechts. Alles, was der Schreibkopf nach rechts hin schreibt, ist der Output des Automaten.
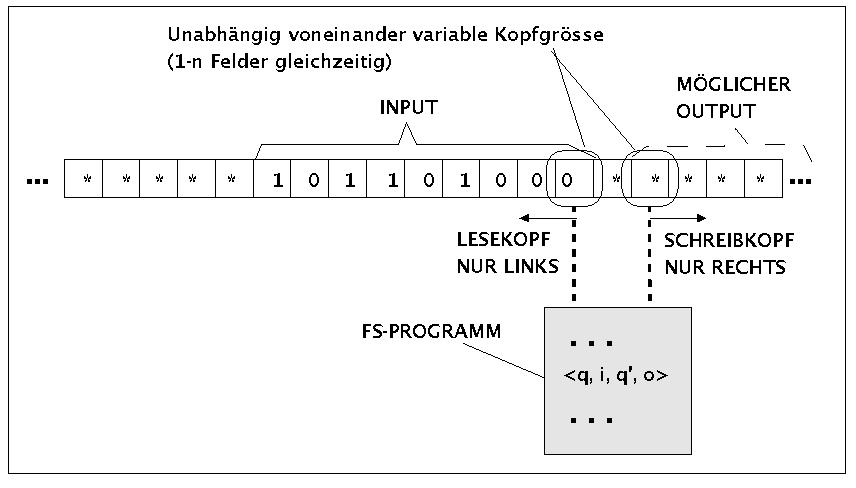
Die 'Idee' eines sequentiellen bzw. endlichen Automaten. Im Bild ist die Variante dargestellt, in der der Automat statt 1 Feld zugleich auch k-viele Felder Lesen bzw. Schreiben kann.
Das Programm eines endlichen Autmaten ähnelt dem einer Turingmaschine, nur fehlen hier die Richtungsangaben für den Lese-Schreib-Kopf. In der folgenden Formalisierung kann man die Ähnlichkeit mit der Turingmaschine sofort erkennen. Sämtliche Begriffe sind übertragbar; man muss nur einige Besonderheiten des endlichen Automaten übertragen, die sich aus der fehlenden 'Eigenbewegung' ergeben.
FSM(t) gdw t = < < Q, E, I, O, {§}, {q0 } >, < P > >
mit
Q:= endliche nichtleere Menge von Zuständen
E := Menge der Endzustände; E C Q & E != 0
I:= endliches Eingabe-Alphabet; |I| > 0
O:= endliches Ausgabe-Alphabet; kann leer sein
B = I u {§}; das endliche Bandalphabet
§ := das leere Zeichen
q0 := der Anfangszustand; q0 in Q
P ist das Programm des endlichen Automaten t und es gilt
P: (Q -E) x B --->
Q x O
Speziell beim endlichen Automaten interessiert auch die folgende Aufspaltung von P in zwei Teilfunktionen F und
G:
P = F u G
mit
F: (Q -E) x B ---> Q
G: (Q -E) x B ---> O
Die Funktion F berechnet zu einem aktuellen Zustand q und zu einem aktuellen Input i den Nachfolgezustand q'. Entsprechend die
Funktion G den neuen Output o.
PRules C P; Die Produktionsregeln PRules sind eine Teilmenge des Programms P
Production(p) gdw p in PRules; p ist eine Produktion (Production), wenn p Element der Produktionsregeln ist; statt von 'Produktion' spricht man auch oft von 'Übergangsregel'
p in PRules ==> p = <si,a,sj,b> mit actual_state(p) = si
States = {s | s C PRules & (A:x,x')(x,x' in s ==> actual_state(x) = actual_state(x') }
k ist eine Konfiguration einer endlichen Maschine m: CONFIGURATION(k,m) gdw m ist ein endlicher Automat & k ist eine Zeichenkette 'aqb§g' mit a,b aus I* und g aus O* und q aus Q. 'aqb' repräsentiert den Input mit der aktuellen Position des Lesekopfes und Zustandes q unter dem ersten Zeichen rechts von b sowie dem aktuellen Output g mit dem Schreibkopf rechts vom letzten Zeichen von g. Folgende Fälle sind hier zu unterscheiden:
q ist der Startzustand q0 und die Konfiguration hat die Form 'aq§' mit dem Lesekopf unter dem ersten Zeichen rechts von a und dem Schreibkopf rechts vom ersten Blank rechts von a.Dies nennen wir eine Startkonfiguration ('START_CONFIGURATION') und a die Eingabe der Turingmaschine;
q ist ein Endzustand und und die Konfiguration hat die Form 'qab§g' mit dem Lesekopf links von dem ersten Zeichen von a und dem Schreibkopf rechts vom letzten Zeichen von g, wobei g leer sein kann. Dies nennen wir auch eine Endkonfiguration ('END_CONFIGURATION') und g das Ergebnis;
q ist weder Start- noch Endzustand.
Die Menge der Konfigurationen ('configurations') eines endlichen Automaten m: configurations(m) = { k | CONFIGURATION(k,m) }
Direkte
Nachfolgekonfiguration eines endlichen Automaten m: eine 'direkte Nachfolgekonfiguration' von aqb§g ist die
Zeichenkette a'q'b'§g', wenn a'q'b'§g' aus aqb§g durch Anwendung einer Übergangsregel di
entstanden ist. Man schreibt:
Die neue Konfiguration unterscheidet sich von der vorhergehenden Konfiguration maximal durch eine neue Position des Lesekopfes und möglicherweise durch eine Veränderung des des Schreibkopfes mit Veränderung des Outputs
P ist ein Protokoll ('protocol') mit der Länge n von dem endlichen Automaten m für die Eingabe x : PROTOCOL(P,m,x,n) gdw P ist ein Tupel der Länge n & rn(P) C configurations(m) & (A:i)( i in dm(P) ==> ki |-- ki+1 mit i < n )
k' ist die Nachfolgekonfiguration von k bei einem endlichen Automaten m oder k' ist ableitbar von k mit einem
endlichen Automaten m: ABL(k',k,m) gdw (E:P,n)( PROTOCOL(P,m,k,n) & END_CONFIGURATION(k',m) & k' = Pn. Statt
ABL(k',k,m) schreibt man auch:
n ist die Länge ('length') einer Ableitung eines endlichen Automaten m für die Eingabe k: k |*--m k' ==> lenth(k,k',m) = n gdw (E:P) PROTOCOL(P,m,k,n)
Der INPUT x eines endlichen Automaten m: INPUT(x,m) gdw FSM(m) & '§aq0§' ist eine Startkonfiguration von m
Rechenzeit: die Rechenzeit eines endlichen automaten FSA ist die Zahl der Zustandsübergänge, bis der FSA, angesetzt auf die Eingabe k mit dem Ergebnis k' stoppt. Da jeder endlichen Berechnung eine Ableitung korrespondiert, kann man auch sagen, die Rechenzeit entspricht der Länge der Ableitung von k' aus k unter m.
Die Eingabe x wird von einem endlichen Automaten m akzeptiert ('accepted'): ACCEPT(x,m) gdw FSM(m) & §xq0§ |*-- §qex§g & qe in E und 'g' steht für 'YES'
Die Eingabe x wird von einem endlichen Automaten m nicht akzeptiert ('rejected'): REJECT(x,m) gdw FSM(m) & §xq0§ |*-- §qex§g & qe in E und 'g' steht für 'NO'
Die von einem endlichen Automaten m erkannte Sprache L: L(m) = { x | FSM(m) & ACCEPT(x,m) }
Analog zum Fall des Turingmaschinenprogramms kann man auch das Programm eines endlichen Automaten dirtekt in ein Zustandsdiagramm übertragen. An den Übergangspfeilen zwischen zwei Zustandskreisen fehlt gegenüber dem Fall der Turingmaschine nur die Angabe der Richtung der Lese-Schreib-Köpfe, da diese festliegt.
Als Vorgriff auf die nächste Vorlesung sei hier schon einmal ein erstes Beispiel eines endlichen Automaten gegeben, der die Worte der Sprache L(g4) erkennen kann. Der endliche Automat wird als Zustandsgraph angegeben.
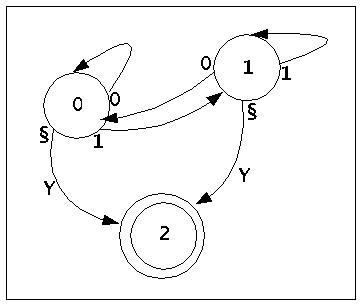
Endlicher Automat für die Sprache L(g4)
Der Automat startet vereinbarungsgemäss im Zustand 0; erkennt er nur ein Blank (§), geht er direkt in den Endzustand und schreibt 'Y'. Erkennt er nur Nullen, bleibt er im Zustand 0, bis er entweder auf ein Blank trifft oder auf eine 1. Dies führt zum Zustand 1. Der kann durch ein Blank beendet werden (Ausgabe 'Y'), oder führt wieder zurück zu einer 0. Bei den Übergängen von 0 nach 1 bzw. von 1 nach 0 druckt erimmer nur ein Blank (§) auf das Ausgabeband.
Definieren sie eine Sprache L3 vom Typ3 als eine Menge von terminalen Worten über einem Alphabet T3
Konstruieren sie einen Syntaxbaum zur Herleitung der terminalen Worte der Sprache L3.
Konstruieren sie eine Grammatik vom Typ3 für die Sprache L3.
Konstruieren Sie den Zustandsgraphen eines endlichen Automaten DTM3, der die Worte der Sprache L3 erkennt.
Übersetzen Sie den Zustandsgraphen des Autmaten DTM3 in ein Programm des Automaten DTM3.
Überlegen sie sich, wie Sie das Programm des endlichen Automaten DTM3 in der Sprache C (oder Java) implementieren könnten.