|
|
GRUNDLAGEN DER INFORMATIK WS 0203 - Vorlesung
|
Nach einer Einführung in die grundsätzliche Funktionsweise eines Computers und der Kommunikation in Netzwerken beschäftigen sich die letzten drei Vorlesungen eher mit grundsätzlichen Themen im Umfeld der Fragen nach der prinzipiellen Leistungsfähigkeit von Computern.
Die erste Vorlesung hatte deutlich gemacht, dass Computer grundsätzlich das Potential besitzen, die Lernfähigkeit von biologischen Gehirnen nachzubilden. Bislang ist die Informatik nur noch nicht in der Lage, dieses Potential tatsächlich zu nutzen.
In der zweiten Vorlesung wurde das Problem der Intelligenz eines Computers am Beispiel des Textlernens weiter untersucht. Es wurde deutlich gemacht, dass zum Erlernen einer Sprache sehr viel 'Vorwissen' darüber gegeben sein muss, was und wie man lernen soll. Die 'Lernunfähigkeit' von Computern besteht einmal mehr nicht darin, dass sie grundsätzlich nicht lernen könnten, sondern darin, dass die Informatik noch zu wenig darüber weiss, welche Voraussetzungen man in ein Programm hineinstecken muss, damit es bestimmte Dinge lernen kann.
In der heutigen letzten Vorlesung geht es um vergleichsweise 'einfache' Dinge, nämlich um einen Überblick über wichtige Datenmodelle, mit denen man Daten in einem Computer so abspeichern kann, dass man sie 'hinreichend schnell' wiederfindet bzw. die Daten erweitert bzw. auch Daten wieder löscht. Dieses Thema kann man auch als ersten Ausblick verstehen auf die Vorlesung 'Algorithmen und Datenstrukturen', die im kommenden Sommer-Semester angeboten werden wird.
Ein elementares Thema der 'klassischen' Informatik ist das Suchen nach bestimmten Daten in einer Datenmenge, das Hinzufügen neuer Daten oder auch das Löschen alter Daten. Die typische Anwendungssituation ist im folgenden Schaubild festgehalten.
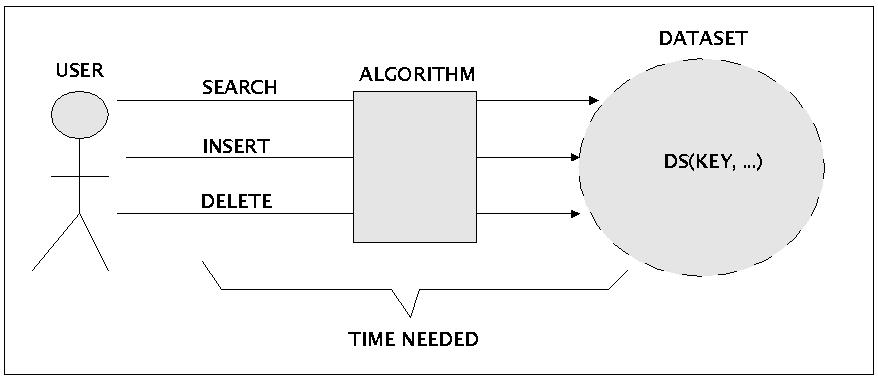
Benutzung von Daten aus Sicht des Benutzers
Unter Zuhilfenahme eines Computers, genauer: eines Programms, sprich eines Algorithmus, versucht ein Benutzer in einer Datenmenge bestimmte Daten wiederzufinden ('search'), zu dieser Menge eventuell neue Daten hinzuzugügen ('insert') oder bestimmte Daten zu löschen ('delete').
Voraussetzung für alle diese Aktionen ist, dass die Daten mit einem identifizierenden Merkmal --einem sogenannten 'Schlüssel' ('key')-- verbunden sind, so dass sie anhand dieses Schlüssels wieder gefunden werden können. Als Schlüssel können Zahlen dienen, Namen bzw. irgendwelche alphanumerische Zeichenketten, mittels deren man einen Schlüssel realisiert.
Solange es sich nur um wenige Datenelemente handelt, spielt die Art und Weise, wie man die Daten anordnet, bei der heutigen Leistungsfähigkeit der Computer kaum eine Rolle. Bei grösseren Datenmengen (einige Hundertausend, Millionen oder mehr) gewinnt der Zeitfaktor aber ein zunehmendes Gewicht. Dann kann es plötzlich bedeutsam werden, wie man Daten in einer Datenmenge abgelegt hat bzw. wie ein Algorithmus aufgebaut ist, um die Operationen wie 'search', 'insert' und 'delete' in einer befriedigenden Zeit auszuführen. Für sich genommen ist der Ausdruck 'befriedigenden Zeit' sehr vage. Er gewinnt aber an Kontur, wenn man ihn in bestimmte Kontexte stellt. Zur Charakterisierung des Zeitbedarfs von Algorithmen bei der Lösung eines Problems haben die Informatiker eine bestimmte Begrifflichkeit eingeführt.
Sei T(n) die Ausführungszeit eines Algorithmus, um ein Problem mit n Elementen zu bearbeiten. Dann interessiert es den Anwender, in welcher Weise mit wachsendem n die Ausführungszeit zunimmt. Folgende vier Fälle werden in der Informatik typischerweise unterschieden:
(Gross-Oh) T(n) = O(f(n)) ; die Ausführungszeit T(n) wächst schneller oder gleich schnell (>=) wie eine Funktion f(n), die das Verhalten von n beschreibt. Man sagt, T(n) entspricht 'Gross O von f(n)'. Genauer, es gibt positive Konstanten c und n0 so dass T(n) <= c*f(n) mit n > n0.
(Gross Omega) T(n) = Omega(f(n)); die Ausführungszeit T(n) wächst schneller oder gleich schnell (<=) wie eine Funktion f(n), die das Verhalten von n beschreibt. Man sagt, T(n) entspricht 'Omega von f(n)'. Genauer, es gibt positive Konstanten c und n0 so dass T(n) >= c*f(n) mit n > n0.
(Gross Theta) T(n) = Theta(f(n)); die Ausführungszeit T(n) wächst gleich schnell (=) wie eine Funktion f(n), die das Verhalten von n beschreibt. Man sagt, T(n) entspricht 'Theta von f(n)'. Genauer, es gibt positive Konstanten c und n0 so dass T(n) = c*f(n) mit n > n0.
(Klein o) T(n) = o(f(n)); die Ausführungszeit T(n) wächst langsamer (<) wie eine Funktion f(n), die das Verhalten von n beschreibt. Man sagt, T(n) entspricht 'Theta von f(n)'. Genauer, es gibt positive Konstanten c und n0 so dass T(n) < c*f(n) mit n > n0.
In der Praxis relevant sind vor allem folgende Funktionen:
Konstant O(c): ein einzelner Befehl wird normalerweise mit O(1) veranschlagt.
Logarithmisch O(log(n)): die Basis des Logarithmus spielt in dieser Schreibweise keine Rolle; die Aussage gilt für jedes Basis! Eine logarithmische Ausführungszeit ist jedenfalls deutlich kürzer als eine lineare (siehe unten).
Linear O(n)
n-log-n O(n * log(n)): n-log-n ist schon sehr ungünstig, aber in vielen Fällen noch brauchbar.
Quadratisch O(n2): quadratische, oder gar dann kubische und noch längere Ausführungszeiten, ie z.B. exponentielle (O(2n)), sind für grosse Zahlen in der Praxis normalerweise nicht mehr ausführbar.
Es fragt sich dann, welche Datenmodelle stehen der Informatik zur Verfügung, um Daten so abzuspeichern, dass die Operationen search/ insert/ delete in akzeptabler Zeit ausführbar sind?
An dieser Stelle kann man eine grundsätzliche Unterscheidung treffen: die Daten sind 1-dimensional angeordnet oder n-dimensional mit n > 1.
Beispiele für 1-dimensionale Anordnungen wären z.B. ein Feld ('array'), eine Warteschlange ('queue', 'fifo', 'lifo'), ein Stapel ('stack') oder eine Liste ('list'). Charakteristisch für 1-dimensionale Anordnungen ist, dass ein einzelnes Element X nur dadurch gefunden werden kann, dass man im schlimmsten Fall ('worst case') alle Elemente der Liste eins nach dem anderen absuchen muss, um das Element X zu finden bzw. um am Ende der Liste festzustellen, dass es nicht in der Liste ist. Operationen über 1-dimensionalen Anordnungen mit n Elementen können also lineare Zeit beanspruchen, d.h. O(n). Dies bedeutet nun nicht, dass die soeben genannten Datenelemente völlig nutzlos sind. Es gibt typische Anwendungen, wo sie geradezu unverzichtbar sind. Nur für den Fall des Speicherns von grossen Datenmengen stellen sie keine optimale Lösung dar, da es andere Datenmodelle höherer Dimensionalität gibt, die weniger Zeit beanspruchen.
n-dimensionalen Anordnungen können hier erheblich günstigere Operationszeiten bieten. Im folgenden soll dies am Beispiel von 2-dimensionalen Datenmodellen illustriert werden. 2-dimensionale Datenmodelle sind im allgemeinen Fall Graphen. Für den konkreten Einsatz benutzt man allerdings Bäume, und zwar binäre Bäume. Warum binäre Bäume?
In einer informellen Charakterisierung kann man sagen, dass Bäume verallgemeinerte Listenstrukturen sind. Ein Element ---üblicherweise spricht man von Knoten --- hat nicht, wie im Falle linearer Listen, nur einen Nachfolger, sondern eine endliche, begrenzte Anzahl von sogenannten Söhnen. In der Regel ist einer der Knoten als Wurzel des Baumes ausgezeichnet. Das ist zugleich der einzige Knoten ohne Vorgänger. Jeder andere Knoten hat einen (unmittelbaren) Vorgänger, der auch Vater des Knotens genannt wird. Eine Folge von Knoten eines Baumes heißt Pfad. Jeder von der Wurzel verschiedene Knoten eines Baumes ist durch genau einen Pfad mit der Wurzel verbunden. Man kann Bäume als spezielle planare, zyklenfreie Graphen auffassen. Die Knoten des Baumes sind die Knoten des Graphen; je zwei Knoten p und q sind durch eine Kante miteinander verbunden, wenn q Sohn von p (und damit p Vater von q) ist.
Ist unter den Söhnen eines jeden Knotens eines Baumes eine Anordnung definiert, so dass man vom ersten, zweiten, dritten usw. Sohn eines Knotens sprechen kann, so nennt man den Baum geordnet. Dies darf man nicht mit der Ordnung eines Baumes verwechseln. Darunter versteht man nämlich die maximale Anzahl von Söhnen eines Knotens. Besonders wichtig sind geordnete Bäume der Ordnung 2; sie heißen auch binäre Bäume oder Binärbäume. Statt vom ersten und zweiten Sohn spricht man bei Binärbäumen vom linken und rechten Sohn eines Knotens. Im Normalfall sind Bäume endlich, d.h. es gibt Knoten, die keine Söhne mehr haben; diese Knoten nennt man äussere Knoten, Endknoten oder Blätter. Alle anderen Knoten ausser den Endknoten sind die inneren Knoten.
Die Menge der Bäume ('trees') TREE ist wie folgt gegeben:
Ein einziger Knoten k der Ordnung d ist in TREE
Wenn t in TREE ist und die Ordnung d hat und t1, ..., tk sind in TREE und haben die Ordnung d, dann ist auch t' in TREE, wobei t' dadurch entsteht, dass man einen Endknoten k aus t so mit den Bäumen t1, ..., tk verknüpft, dass jede Kante von k mit einem Baum aus t1, ..., tk verbunden ist.
Nur was nach (1) und (2) gebildet wurde ist ein Baum.
Jeder Baum t', der über eine Kante mit einem Knoten in einem Baum t verbunden ist, ist ein Teilbaum von t.
Die Höhe h eines Baumes ist der maximale Abstand eines Endknotens zur Wurzel.
Die Tiefe d eines Knotens ist der Abstand des Knotens zur Wurzel, d.h. die Anzahl der Kanten.
Alle Knoten eines Baumes t mit der Tiefe d bilden das Niveau (die Ebene, den Level) d des Baumes t.
Ein Baum heisst vollständig, wenn auf allen Niveaus die maximale Anzahl von Knoten vorhanden ist und alle Endknoten die gleiche Tiefe besitzen.
Der Hauptzweck von Bäumen besteht im allgemeinen darin, dass man in jedem Knoten einen Schlüssel (key) so abspeichern kann, dass man ihn nach einer festen Regel wiederfinden kann.
Binäre Bäume sind Bäume der Ordnung d=2. Binäre Bäume werden zu binären Suchbäumen dadurch, dass man für die Schlüssel der Knoten eine bestimmte Ordnung fordert:
t ist ein Binärer Suchbaum ('binary searchtree') BSTREE genau dann, wenn gilt:
BSTREE C TREE & d=2.
Jeder Knoten k von t aus BSTREE enthält einen Schlüssel ('key')
Für jeden Knoten k von t mit nachfolgenden Teilbäumen tleft, tright gilt, dass die Schlüssel aller Knoten aus dem linken Teilbaum tleft kleiner sind als der Schlüssel von k und der Schlüssel von k wiederum kleiner ist als die Schlüssel aller Knoten aus dem rechten Teilbaum tright.
Die Schlüssel von Endknoten besitzen einen exklusiven Wert.
Bäume, in denen die Schlüssel in den Blättern gespeichert sind, nennt man Blattsuchbäume [OTTMANN/WIDMAYER 2002:255]
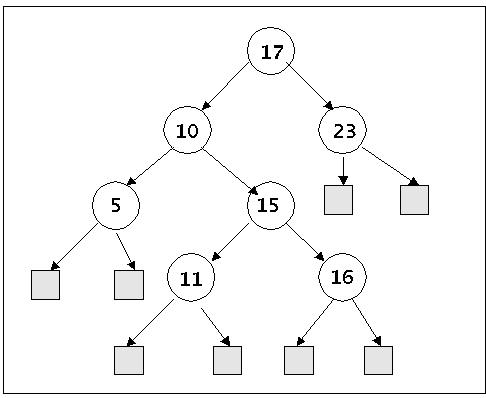
Binärer Suchbaum
Der binäre Suchbaum im Bild enthält 7 Elemente. Um festzustellen, dass ein bestimmter Schlüssel (z.B. '14') nicht im Baum vorkommt, benötigt man höchstens 3 Vergleiche. Und man kann schon aus diesem einfachen Beispiel erahnen, dass die Verarbeitungszeiten bei Bäumen offensichtlich mit der Höhe h eines Baumes zu tun haben.
Ist die Höhe h eines Baumes gegeben, dann gilt für einen vollständigen binären Baum, dass die anzahl n der Knoten sich wie folgt berechnet: n = 2h+1-1
Ist die Anzahl n der Knoten gegeben, dann berechnet sich für einen vollständigen binären Baum die Höhe h wie folgt: h = (log2 n+1) - 1.
Mit Bezug auf die Höhe des Baumes gilt dann für die Ausführungszeit: T(n) = O(log(n)). Diese logarithmische ausführungszeit ist deutlich günstiger als eine lineare Zeit O(n), die im Falle von Operationen über Listen auftreten kann. Dies spricht für Naumstrukturen. Eine solche günstige Ausführungzeit ist bei binären Bäumen im allgemeinen aber nur garantiert, wenn der Baum 'ausgeglichen' bzw. 'balanciert' ist. Damit ist gemeint, dass die Struktur des Baumes so sein muss, dass für alle denkbaren Anfragen eine maximale Ausführungszeit gegeben ist, konkret, dass alle Pfade 'annähernd gleich' sind.
Für die Charakterisierung der 'Ausgeglichenheit' von Bäumen wurden unterschiedliche Eigenschaften herangezogen, z.B. die Höhe der Teilbäume, ihre Gewichte oder bestimmte Farbverteilungen.
Im Falle der Benutzung des Gewichtes gilt z.B.: Wenn p ein Knoten des Baumes T ist und Wurzel des Teilbaumes Tp, dann schreibt man W(p) bzw. W(Tp) für die Menge der Endknoten von Tp. Ist T ein Baum mit dem linken Teilbaum Tl dann ist die Wurzelbalance rho(T) = W(Tl)/W(T). Und der binäre Suchbaum T heisst gewichtsbalanziert mit alpha, wenn für jeden Teilbaum von T' von T gilt: alpha < rho(T') < (1-alpha). Bei der Schreibweise BB[alpha] kann alpha im Intervall [1/4, 1-(sqrt(2)/2)] liegen (vgl. z.B. [OTTMANN/WIDMAYER 2002:303]).
Da die günstige Ausführungszeit von binären Bäumen davon abhängig ist, dass sie ausbalanziert sind, muss man sicherstellen, dass diejenigen binären Bäume, mit denen man arbeiten will, diese Eigenschaft in allen Phasen der Nutzung besitzen, d.h. sie müssen diese Eigenschaft während aller Operationen (speziell Einfügen und Löschen) erhalten. Bäume, die so beschaffen sind, sollen (dynamisch) ausbalanzierte binäre Suchbäume genannt werden.
Einige wichtige Beispiele von (dynamisch) balanzierten binären Suchbäumen.
Die Forschungen zu ausgeglichenen (balancierten) Bäumen sind sehr rege. Ständig werden neue Datenmodelle entwickelt. Hier einige Ordnungskriterien, anhand deren man die Vielzahl der angebotenen Algorithmen anordnen könnte: :
+/- balanciert: behandelt der Algorithmus Bäume, die ausgeglichen sind oder nicht
+/- Blattsuchbaum: die Schlüssel liegen entweder in den inneren Knoten oder in den Endknoten
+/- externe Daten: die Daten sind alle im Arbeitsspeicher oder stammen (teilweise oder überwiegend) aus externen Speichern.
+/- Multiuser: nur ein Prozess greift gleichzeitig auf die Datenmenge zu oder mehrere; im letzteren Fall ist es entscheidend, ob die verschiedenen Prozesse interagieren können.
+/- n-dimensionale Strukturen mit n > 2: für viele geometrische (aber auch andere) Problemstellungen unabdingbar.
+/- Zeitbedarf
Die nachfolgende Liste von bislang untersuchten Algorithmen ist nicht vollständig und auch noch nicht systematisch anhand der zuvor herausgestellten Kriterien organisiert.
AVL-Bäume, historisch ältester Vorschlag, so genannt nach ihren Erfindern G.M.Adel'son-Vel'skii und E.M.Landis (1962) [KNUTH 1973:III-451]. Die Grundidee besteht hier darin, dass man die Pfadlängen so gestaltet, dass die Höhe des linken Unterbaumes eines Knotens +/-1 der Höhe des rechten Unterbaumes ist. Entstehen bei Einfügungen oder Löschungen Abweichungen von dieser Forderung, dann werden die Knoten 1-2 mal 'rotiert', um die geforderte Eigenschaft wieder herzustellen. Die benötigte Ausführungszeit bemisst sich nach O(lg n).
(1-2-)Bruder-Bäume als expandierte AVL-Bäume; alle Endknoten haben die gleiche Tiefe; es können auch begrenzt unäre Knoten auftreten (vgl. [OTTMANN/WIDMAYER 2002:287]). Einfügen und entfernen eines Knoten benötigt benötigt in einem 1-2-Bruder-Baum O(log(n)).
Gewichtsbalancierte binäre Suchbäume (vgl. [OTTMANN/WIDMAYER 2002:287]). Es gilt, dass die Höhe von gewichtsbalancierten Bäumen logarithmisch in der Anzahl der Blätter oder Knoten beschränkt ist (vgl. z.B. [OTTMANN/WIDMAYER 2002:305]). Das Einfügen und Entfernen eines Knoten benötigt O(log(n)). Die gemittelte Anzahl von Rotationen und Doppelrotationen ist konstant.
Randomisierte binäre Suchbäume nach Aragon und Seidel (1986). Das suchen eines Knoten benötigt O(log(n). Die gemittelte Anzahl von Rotationen ist kleiner 2 (vgl. z.B. [OTTMANN/WIDMAYER 2002:310-318]).
Selbstanordnende Bäume - Splay-Bäume, diese schieben die häufiger auftretenden Schlüssel zur Wurzel hin. Zu Beginn und in degenerierten Fällen kann die worst-case Suchzeit zwar Omega(n) betragen, aber diese Bäume optimieren sich so, dass sich die Suchkosten von denen optimaler Bäume nur um einen konstanten Faktor unterscheiden (vgl. [OTTMANN/WIDMAYER 2002:318-330]).
2-3-Bäume nach HOPCROFT (1970), zitiert von [KNUTH 1973:III-468]. 2-3-Bäume sind vollständige binäre Bäume und jeder Knoten kann bis zu 2 Schlüsseln besitzen (Spezialfall von B-Bäumen).
Top-Down 2-3-4-Bäume stellen eine Verallgemeinerung von 2-3-Bäumen dar (siehe [SEDGEWICK 1992:256]). Ein 4-Knoten kann bis zu 3 Schlüsseln enthalten und besitzt 4 Verknüpfungen zu seinen Kindern. Für die Suche in 2-3-4-Bäumen benötigt man eine Zeit von O(lg n), für das Einfügen benötigt man weniger als lg(n+1) Aufspaltungen und empirische Ergebnisse deuten auf weniger als 1 Aufspaltung eines Knoten hin (Spezialfall von B-Bäumen).
Rot-Schwarz-Bäume von Guibas/ Sedgewick (1978) stellen einen Versuch dar (neben dem Schichtemodell von Leeuwen und Overmars (1983)), unterschiedliche Klassen von balancierten Bäumen (AVL, 2-3-4-Bäume, B-Bäume usw.) einheitlich zu repräsentieren. Eine Suche in einem Rot-SChwarz-Baum mit N Knoten und zufälligen Schlüsseln, erfordert etwa log(N) Vergleiche und ein Einfügen erfordert im Durchschnitt weniger als eine Rotation. Eine Suche in einem Rot-Schwarz-Baum mit N Knoten und nicht zufälligen Schlüsseln, erfordert weniger als 2*log(N+2) Vergleiche und die Zahl der Einfügungen liegt unter einem Viertel der Zahl der Vergleiche. Die Zahl der Aufspaltungen entspricht im ungünstigsten Fall dem Fall der Aufspaltungen von 3-4-Knoten bei 2-3-4-Bäumen (siehe dort)[SEDGEWICK 1992:269f].
AA-Bäume stellen gegenüber Rot-Schwarz-Büumen eine deutliche Vereinfachung in Punkto Implementierung dar. Sie unterscheiden sich von Rot-Schwarz-Bäumen nur durch die Forderung, dass linke Söhne nicht rot sein dürfen [WEISS 2000:685ff].
Bottom-up 2-3-4-Bäume sind ähnlich wie Top-Down 2-3-4-Bäume, nur benötigen sie maximal eine Rotation pro Einfügung oder Löschung (siehe [SEDGEWICK 1992:270]).
Top-Down-B-Bäume wurden von R.Bayer und E.McCright eingeführt und lassen sich nach [SEDGEWICK 1992:308] auffassen als externe ausbalanzierte Bäume, die sich mit dem Algorithmus für 2-3-4-Bäume so realisieren lassen dass sich pro Knoten 1- M-1 Schlüssel verwalten lassen. Ein Suchen oder Einfügen in einen B-Baum der Ordnung M mit N Datensätzen erfordert garantiert weniger als logM/2(N+1) Plattenzugriffe. Ein B-Baum der Ordnung M mit N zufälligen Datensätzen hat im Durchschnitt ungefähr 1.44 * N/M Knoten [SEDGEWICK 1992:310]. Die mittlere Anzahl von Teilungsoperationen ist konstant. Die Speicherplatzausnutzung im Falle von nicht randomisierten Folgen kann allerdings schlecht sein, d.h. die inneren Knoten der Ordnung m haben im Schnitt nur (m/2)-1 viele Schlüssel. [OTTMANN/WIDMAYER 2002:331-339]
Dichte Bäume: Bruder-Bäume und B-Bäume haben die Schwäche, dass sie die mögliche Anzahl von Kanten meist nicht ausnutzen. Um diesen Ausnutzungsgrad zu erhöhen --also die Dichte zu erhöhen-- wurden Verfahren ausgearbeitet, die es erlauben, vollständigen Bäumen beliebig nahe zu kommen [OTTMANN/WIDMAYER 2002:340].
Single-User-Bäume: alle jene Bäume, bei denen eine Such-, Einfüge- oder Löschaktion abgeschlossen sein muss, bevor eine neue Such-, Einfüge- oder Löschaktion gestartet werden kann. Dies trifft auf nahezu alle bisher genannten Bäume zu.[OTTMANN/WIDMAYER 2002:345-47].
Multi-User-Bäume: alle jene Bäume, bei denen eine Such-, Einfüge- oder Löschaktion parallel und in beliebiger Reihenfolge gestartet werden kann. Eine Variante solchr Multi-User Bäume kann dadurch entstehen, dass man in Single-User-Bäumen Sperrstrategien integriert, die noch nicht abgeschlossene Restrukturierungsmassnahmen vor neuen Anforderngen abblockt [OTTMANN/WIDMAYER 2002:347]. Eine deutliche Verbesserung bringen bei Single-User-Systemen hingegen reine Top-Down Verfahren, die ein Zurücklaufen ('backtracking') vermeiden. In diesem Kontext erweisen sich Blattsuchbäume als besonders günstig [OTTMANN/WIDMAYER 2002:347]. Einen Kompromiss stellen relaxierte Balancierungsverfahren dar (J.L.W.KESSELS (1983), O.NOURNI/ E.SOISALON SOININEN/ D.WOOD (1987, 1991), L.KASEN/ R.FAGERBERG (1994, 1995)), bei denen die Restrukturierungsmassnahmen abgetrennt im Hintergrund ablaufen; hier können phasenweise Bäume auftreten, die nicht mehr balanciert sind [OTTMANN/WIDMAYER 2002:347f].
Multi-User-Bäume als Stratifizierte Bäume: von S.HANKE/ TH.OTTMANN/ E.SOISALON-SOININEN (1996) stellen ein besonders elegantes Verfahren von Multi-User-Bäumen dar [OTTMANN/WIDMAYER 2002:348-62]. Z-Stratifizierte Bäume sind Blattsuchbäume, deren verschiedene Schichten auch Strassen genannt werden. Diese Bäume sind identisch mit der Klasse der symmetrischen B-Bäume, der Klasse der halbbalancierten Bäume sowie mit der Klasse der Rot-Schwarz-Bäume, sieht man von den jeweiligen Update-Verfahren ab [OTTMANN/WIDMAYER 2002:349]. Die Höhe Z-Stratifizierter Bäume ist in der Grössenordnung O(log(n)). Als Strukturänderungen zählen nur die Änderungen von Zeigern, nicht Farbänderungen. Die Einfügung und Löschung von Knoten werden als Forderungen mittels Markierungen realisiert. Wann und in welcher Reihenfolge diese Forderungen realisiert werden ist bis auf einige spezielle Fälle variabel. Z-Stratifizierter Bäume wachsen immer an der Wurzel 'nach oben'. Neue Schlüssel werden immer an den Endknoten eingeführt und dort werden auch zu beseitigende Schlüssel herausgezogen [OTTMANN/WIDMAYER 2002:359]. Man kann zeigen, dass eine beliebige Abfolge von Einfüge- und Löschoperationen mit abschliessenden Korrekturen nicht mehr Zeit benötigt, als wenn man diese Korrekturen sofort nach jeder Operation ausführen würde. Ihn vielen Fällen sind überhaupt keine Restrukturierungsoperationen nötig [OTTMANN/WIDMAYER 2002:362].
Eindeutig repräsentierte Wörterbücher: Bäume, über die die Operationen Suchen, Einfügen und Löschen erklärt sind, nennt man auch Wörterbücher. Für Wörterbücher sind Eigenschaften interessant wie mengeneindeutig (Reihenfolge der Operationen beliebig), grösseneindeutig (impliziert Mengeneindeutigkeit) oder gar ordnungs-eindeutig [OTTMANN/WIDMAYER 2002:362]. Solche Wörterbücher wurden von SNYDER (1977) untersucht und später von OTTMANN/WIDMAYER optimiert. Zugrunde liegen keine Bäume mehr sondern geordnete Listen. Für 3-Ebenen-Sprunglisten ergibt sich für alle Operationen dann die Ausführungszeit O(n1/3 )
Alphabetische Suchbäume (Tries , retrieval): diese sind dort von Interesse, wo es darum geht, grosse Mengen von Wörtern aus Texten kompakt zu speichern [OTTMANN/WIDMAYER 2002:374f].
N-dimensionale Bäume: für viele, nicht nur geometrische, Probleme ist es notwendig, die 'Nähe' von Knoten mit mehreren Schlüsseln mitzukodieren. Dies kann man dadurch erreichen, dass man die k Schlüssel als Dimensionen eines k-dimensionalen Raum es auffasst. [OTTMANN/WIDMAYER 2002:376-79]. Weitere Überlegungen hierzu bei MEHLHORN (1984).
Mit dieser Vorlesung sollte eine erste Idee vermittelt werden, wie das Suchen/ Einfügen/ Löschen von Daten in grossen Datenmengen zeitkritisch bewältigt werden kann. Es wird der vorlesung 'Algorithmen und Datenstrukturen' vorbehalten bleiben, diese Sachverhalte detaillierter darzulegen.
Mit welchen Begriffen wird in der Informatik das Verhältnis zwischen der Ausführungszeit T(n) eines Algorithmus und der Anzahl n der Elemente eines Problems beschrieben?
Wodurch ist das Datenmodell 'Baum' charakterisiert?
Was unterscheidet einen binären Baum von einem Baum?
Was unterscheidet einen binären Such-Baum von einem binären Baum?
Wie lässt sich der Zusammenhang zwischen der Anzahl der Knoten und der Höhe eines binären Baumes beschreiben?
Was zeichnet einen ausgeglichenen Baum aus?
Welche Ordnungskriterien zu binären Suchbäumen fallen Ihnen ein?
Welchen der der charakterisierten Algorithmen zu ausgeglichenen Bäumen erscheint Ihnen für Ihren Arbeitsbereich interessant zu sein?
B.FLAMIG, [1993], "Practical Data Structures in C++",John Wiley & Sons, New York et al.
'D.E.KNUTH, [1973], "The Art of Computer Programming. Vol.3: Sorting and Searching", Addison-Wesley Publ.Company,Reading (MA) et al
Th.OTTMANN/ P.WIDMAYER [2002, 4.Aufl.], "Algorithmen und Datenstrukturen", Spektrum Akademischer
Verlag, Heidelberg - Berlin
/* Exzellentes Buch, das die Probleme aus theoretischer Sicht behandelt und ein
grosses Spektrum von Algorithmen abdeckt, speziell auch neuere Entwicklungen. */
R.SEDGEWICK [1992, 2.Aufl.],
"Algorithms in C++", Addison-Wesley Publ.Company, Bonn - Paris - Reading (MA) et al
/* Solide, aber nicht mehr ganz up to
date; in der Mitte zwischen OTTMANN et al und WEISS; C++-Kode nicht vollständig. */
M.A.WEISS
[2000,2.Aufl.], "Data Structures and Problem Solving using C++", Addison-Wesley Publ.Company, Reading (MA) et al
/*
Exzellentes Buch, das das gesamte Thema behandelt und in allen Abschnitten die Implementierung im Rahmen von C++ vorstellt.
Quellcode weitgehend über das Netz verfügbar. */