
|
|
I-ALGO SS03 - ALGORITHMS AND DATASTRUCTURES - Lecture with Exercises
|
In the last lectures we have dealt with basic datastructures for graphs and some algorithms operating on these datastructures. The next target of our investigation are socalled SPLAY-Trees ('to splay' translates in German to 'ausbreiten', 'ausdehnen', 'spreizen'). The name is caused by a certain operation on the datastructure of SPLAY-Trees, which extends the paths of the tree in a certain way.
The reason why we wanted to investigate the datastructures and algorithms connected to SPLAY-Trees was the idea to have a tree which adjusts itself according to the frequency of the questioned items.
Because SPLAY-Trees are Binary Search Trees (BSTs) --but not balanced BSTs!-- we will first describe Binary search Trees. And although SPLAY-Trees are not balanced BSTs they have been invented to overcome certain shortcuts of balanced BSTs; thus we will have a short look to balanced BSTs exemplified with the socalled AA-Trees (Originally we have used the example of AVL-Trees in the lecture, but because there was not good Sourcecode available to demonstrate these trees I have changed the example from AVL- to AA-Trees).
First we will present an example of a binary search tree to get a first intuitive idea of what a binary search tree is. Then we will give a new formal representation compared to those given in lecture 6. After discussing some of the formal properties we will present some algorithms to represent binary search trees.
A binary search tree is a directed acyclic graph with labels at the vertices, which are in the literature usually called 'nodes'. But because we want to stay in agreement with the preceding formulas we will stay with the terminology of vertices and edges as used with graphs in general.
In the example below we have as labels pairs of integers combined with the letters {'O', 'L', 'R'}. The integers are called 'keys' (or 'values') of the vertices. Usually binary search trees are in the literature only represented with keys, not with these additional letters --one could also use the numbers {0,1,2} instead-- representing the geometrical information to be the left or the right successor of a vertex. For someone observing the diagram of a tree he has a 'natural' geometrical orientation induced by his visual system. The 'formal tree as such' has no geometrical information unless one introduces this information explicitly. This is what happened in the diagram below. If you are looking to sourcecode representing binary trees you will see, that in the sourcecoe the geometrical information is encoded directly in the datastructure by using identifiers like 'leftnode' or 'rightnode' etc.
A binary search tree has only one root-vertex, which is not left (L) or right (R); the root is only the origin (O) and relativ to this origin are the following vertices left or right successors.
Every binary tree has only two successors, also called children. If a is a vertex in a binary tree and b is the left succesor and c the right successor, then is a called the parent of b and c.
For the distribution of the keys in a binary search tree it is postulated that the key of a left child is less compared to the key of the parent and the key of the right child is bigger than the key of the parent.
In the example below has the root-vertex the key 35 and the geometrical information 'O' (:= origin'). The left child of the root has the key 21 and the geometrical information 'L' (:=left). The other child of the root as parent has the key 55 and the geometrical information 'R'. Whether one places a child x with the geometrical information g(x)=R 'visually left' or 'visually right' does not matter; the only important point is, that the child with g(x)=R has a key which is bigger compared to the key of the parent.
Besides this you can see in the diagram how it is searched for the value '77'. Presupposing the above mentioned order of the keys the search is straightforward: if '77' is bigger then the root, then continue searching with the right child, otherwise with the left one. Processing searching in this way you will either find a vertex with the same key or not; in the last case --as in the diagram below-- you will end up at the bottom of the tree; and it is clearly determined whether the new vertex has to be inserted left (if the key is less or equal) or right of the last detected vertex. In the example below is the value '77' less than the key = 105, thus a new vertex with key = 77 can be inserted as the left child of the parent with key = 105.
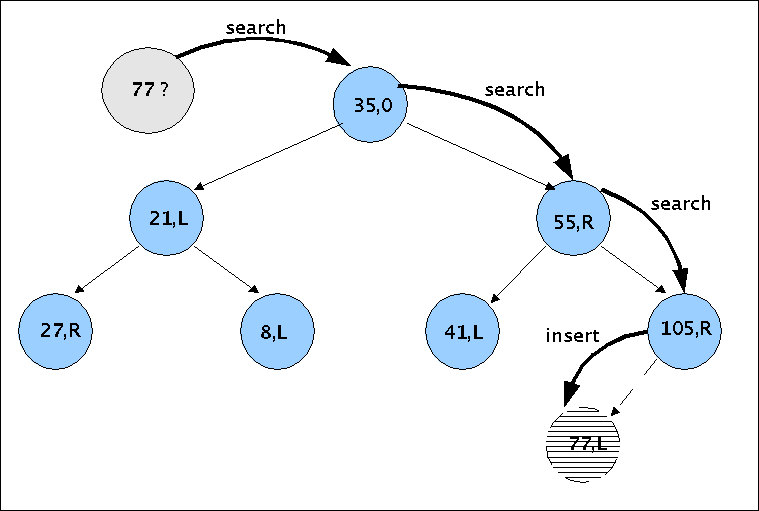
Example of a BST while inserting a node
Having now a first intuitive idea of binary search trees we will give a formal representation. This time we will follow another strategy then in lecture 6. Instead of building the labels into the basic sets itself we are using additional functions for geometrical informations and keys; this approach gives a bit more flexibility.
Def.: BST(t) iff t = < <V, r, K, G >,<E,c,g >
V := vertices(t)
r := root(t) & r in V
K := keys(t); K subset Nat+
G := geo(t), geometrical information = {O,L,R}
E := edges(t), E C V x V & ¬SYM(E)
c := key-function(t), c: V ---> K
g := geometrical-function(t), g: V ---> G
(a,b) in E ==>
Def.: parent(b) = a
Def.: child(a) = b
Def.: SISTERS(x,y) iff
(E:a)( a=parent(x) & a=parent(y) )
(a,b) in E & child(a) = b & g(b) = 'L' ==>
Def.: left_child_of(a) = b
(a,b) in E & child(a) = b & g(b) = 'R' ==>
Def.: right_child_of(a) = b
BST(t) ==>
Def.: PATH(p,x,y,t) iff
x in vertices(t) & n-tupel(p) & x=p0 & y=plength(p) &
(A:i,j)( i,j in dm(p) & j=i+1 ==> pj child_of(pi) )
//A length of a path is the number of vertices in the path minus 1
BST(t) & PATH(p,x,y,t) ==>
Def.: length(p)) = |dm(p)| - 1
//A leaf is a vertex at the 'bottom' of a tree, which has no children
BST(t) ==>
Def.: leafs(t) = {k| k in vertices(t) & (E:p)( PATH(p,root(t),k,t) & ¬(E:k')(child_of(k)=k' )) }
//The path_to(x) goes from the root to the vertex x
BST(t) ==>
Def.: path_to(x) = p iff
(E:p)( PATH(p,root(t),x,t) )
//The path_from(x) goes from x to a leaf
BST(t) ==>
Def.: path_from(x) = p iff
(E:p,k)( PATH(p,x,k,t) & k in leafs(t) )
//The depth of a node x is the number of vertices from the root(t) to x minus 1
BST(t) ==>
Def.: depth(x) = length( path_to(x) )
//The height of a vertex x is the number of vertices on the path from x to a leaf minus 1
BST(t) ==>
Def.: height(x) = length( path_from(x) )
Axioms:
A1://root is not left and not right
g(r) = O
A2://The geometrical information of two sisters is complementary
SISTERS(b,c) ==> [g(b)='L' & g(c)='R'] or [g(b)='R' & g(c)='L']
A3://The key of the left child is less compared to the key of the parent and the key of the parent
is less compared to the right child.
a,b in vertices(t) & b=child_of(a) ==>
[c(b) < c(a) & g(b)='L'] or [ c(b) > c(a) & g(b)='R']
The following example of a sourcecode for binary search trees is taken from the webbased sources accompanying the book [WEISS 2001].
This sourcecode is using the class DESexeptions := the exeption-class of WEISS. The topic of exceptions will be explained in the parallel lecture about C++ next week.
The file BinarySearchTree.hpp defines the node-class and some operations, using the public operations as interfaces to the protected operations.
In the node-class is the element size not necessary for ordinary binary search trees, but it is used for the more specialized version of a binary search tree with rank; in a BST with rank one can search for the k-th element in the whole tree.
//*******************************+
//
// BinarySearchTree.hpp
//
// author: WEISS 2001
// modified for lecture: gerd doeben-henisch
//
// Connected to BinarySearchTree.cpp and BinarySearchTree_usage.cpp
//
//******************************************************
#ifndef BINARY_SEARCH_TREE_H_
#define BINARY_SEARCH_TREE_H_
#include "Wrapper.hpp"
template <class Comparable>
class BinarySearchTree;
template <class Comparable>
class BinarySearchTreeWithRank;
template <class Comparable>
class BinaryNode
{
Comparable element;
BinaryNode *left;
BinaryNode *right;
int size;
BinaryNode( const Comparable & theElement, BinaryNode *lt,
BinaryNode *rt, int sz = 1 )
: element( theElement ), left( lt ), right( rt ), size( sz ) { }
friend class BinarySearchTree<Comparable>;
friend class BinarySearchTreeWithRank<Comparable>;
};
// BinarySearchTree class
//
// CONSTRUCTION: with no parameters or another BinarySearchTree.
//
// ******************PUBLIC OPERATIONS*********************
// void insert( x ) --> Insert x
// void remove( x ) --> Remove x
// void removeMin( ) --> Remove smallest item
// Comparable find( x ) --> Return item that matches x
// Comparable findMin( ) --> Return smallest item
// Comparable findMax( ) --> Return largest item
// bool isEmpty( ) --> Return true if empty; else false
// void makeEmpty( ) --> Remove all items
// ******************ERRORS********************************
// Exceptions are thrown by insert, remove, and removeMin if warranted
template <class Comparable>
class BinarySearchTree
{
public:
BinarySearchTree( );
BinarySearchTree( const BinarySearchTree & rhs );
virtual ~BinarySearchTree( );
Cref<Comparable> findMin( ) const;
Cref<Comparable> findMax( ) const;
Cref<Comparable> find( const Comparable & x ) const;
bool isEmpty( ) const;
void makeEmpty( );
void insert( const Comparable & x );
void remove( const Comparable & x );
void removeMin( );
const BinarySearchTree & operator=( const BinarySearchTree & rhs );
typedef BinaryNode<Comparable> Node;
protected:
Node *root;
Cref<Comparable> elementAt( Node *t ) const;
virtual void insert( const Comparable & x, Node * & t ) const;
virtual void remove( const Comparable & x, Node * & t ) const;
virtual void removeMin( Node * & t ) const;
Node * findMin( Node *t ) const;
Node * findMax( Node *t ) const;
Node * find( const Comparable & x, Node *t ) const;
void makeEmpty( Node * & t ) const;
Node * clone( Node *t ) const;
};
// BinarySearchTreeWithRank class.
//
// CONSTRUCTION: with no parameters or
// another BinarySearchTreeWithRank.
//
// ******************PUBLIC OPERATIONS*********************
// Comparable findKth( k )--> Return kth smallest item
// All other operations are inherited (but C++ requires
// some extra stuff).
template <class Comparable>
class BinarySearchTreeWithRank : public BinarySearchTree<Comparable>
{
public:
Cref<Comparable> findKth( int k ) const;
void insert( const Comparable & x )
{ BinarySearchTree<Comparable>::insert( x ); }
void remove( const Comparable & x )
{ BinarySearchTree<Comparable>::remove( x ); }
void removeMin( )
{ BinarySearchTree<Comparable>::removeMin( ); }
typedef BinaryNode<Comparable> Node;
private:
void insert( const Comparable & x, Node * & t ) const;
void remove( const Comparable & x, Node * & t ) const;
void removeMin( Node * & t ) const;
Node *findKth( int k, Node *t ) const;
int treeSize( Node *t ) const
{ return t == NULL ? 0 : t->size; }
};
#endif
In the internal function find(x,n) I have inserted some printouts for demonstrations during the lecture.
//*******************************+
//
// BinarySearchTree.cpp
//
// -> BinarySearchTree.hpp -> Wrapper.hpp -> Except.hpp , stdlib.h
// -> BinarySearchTree_usage.cpp
//
// author: WEISS 2001
// modified for lecture: gerd doeben-henisch
//
//*************************************+
//
// Comments:
//
// (1) The public finctions are mainly only used to call the private/ protected functions
//
//******************************************************
// Construct the tree.
template <class Comparable>
BinarySearchTree<Comparable>::BinarySearchTree( ) : root( NULL )
{
}
// Copy constructor.
template <class Comparable>
BinarySearchTree<Comparable>::
BinarySearchTree( const BinarySearchTree<Comparable> & rhs ) : root( NULL )
{
*this = rhs;
}
// Destructor for the tree.
template <class Comparable>
BinarySearchTree<Comparable>::~BinarySearchTree( )
{
makeEmpty( );
}
// Insert x into the tree;
// Throws DuplicateItemException if x is already there.
template <class Comparable>
void BinarySearchTree<Comparable>::insert( const Comparable & x )
{
insert( x, root );
}
// Remove x from the tree.
// Throws ItemNotFoundException if x is not in the tree.
template <class Comparable>
void BinarySearchTree<Comparable>::remove( const Comparable & x )
{
remove( x, root );
}
// Remove minimum item from the tree.
// Throws UnderflowException if tree is empty.
template <class Comparable>
void BinarySearchTree<Comparable>::removeMin( )
{
removeMin( root );
}
// Return the smallest item in the tree wrapped in a Cref object.
template <class Comparable>
Cref<Comparable> BinarySearchTree<Comparable>::findMin( ) const
{
return elementAt( findMin( root ) );
}
// Return the largest item in the tree wrapped in a Cref object.
template <class Comparable>
Cref<Comparable> BinarySearchTree<Comparable>::findMax( ) const
{
return elementAt( findMax( root ) );
}
// Find item x in the tree.
// Return the matching item wrapped in a Cref object.
template <class Comparable>
Cref<Comparable> BinarySearchTree<Comparable>::find( const Comparable & x ) const
{
return elementAt( find( x, root ) );
}
// Make the tree logically empty.
template <class Comparable>
void BinarySearchTree<Comparable>::makeEmpty( )
{
makeEmpty( root );
}
// Test if the tree is logically empty.
// Return true if empty, false otherwise.
template <class Comparable>
bool BinarySearchTree<Comparable>::isEmpty( ) const
{
return root == NULL;
}
// Deep copy.
template <class Comparable>
const BinarySearchTree<Comparable> &
BinarySearchTree<Comparable>::
operator=( const BinarySearchTree<Comparable> & rhs )
{
if( this != &rhs )
{
makeEmpty( );
root = clone( rhs.root );
}
return *this;
}
// Internal method to wrap the element field in node t inside a Cref object.
template <class Comparable>
Cref<Comparable> BinarySearchTree<Comparable>::elementAt( Node *t ) const
{
if( t == NULL )
return Cref<Comparable>( );
else
return Cref<Comparable>( t->element );
}
// Internal method to insert into a subtree.
// x is the item to insert.
// t is the node that roots the tree.
// Set the new root.
// Throw DuplicateItemException if x is already in t.
template <class Comparable>
void BinarySearchTree<Comparable>::
insert( const Comparable & x, Node * & t ) const
{
if( t == NULL )
t = new Node( x, NULL, NULL );
else if( x < t->element )
insert( x, t->left );
else if( t->element < x )
insert( x, t->right );
else
throw DuplicateItemException( );
}
// Internal method to remove from a subtree.
// x is the item to remove.
// t is the node that roots the tree.
// Set the new root.
// Throw ItemNotFoundException is x is not in t.
template <class Comparable>
void BinarySearchTree<Comparable>::
remove( const Comparable & x, Node * & t ) const
{
if( t == NULL )
throw ItemNotFoundException( );
if( x < t->element )
remove( x, t->left );
else if( t->element < x )
remove( x, t->right );
else if( t->left != NULL && t->right != NULL ) // Two children
{
t->element = findMin( t->right )->element;
removeMin( t->right ); // Remove minimum
}
else
{
BinaryNode<Comparable> *oldNode = t;
t = ( t->left != NULL ) ? t->left : t->right; // Reroot t
delete oldNode; // delete old root
}
}
// Internal method to remove minimum item from a subtree.
// t is the node that roots the tree.
// Set the new root.
// Throw UnderflowException if t is empty.
template <class Comparable>
void BinarySearchTree<Comparable>::removeMin( Node * & t ) const
{
if( t == NULL )
throw UnderflowException( );
else if( t->left != NULL )
removeMin( t->left );
else
{
Node *tmp = t;
t = t->right;
delete tmp;
}
}
// Internal method to find the smallest item in a subtree t.
// Return node containing the smallest item.
template <class Comparable>
BinaryNode<Comparable> * BinarySearchTree<Comparable>::findMin( Node *t ) const
{
if( t != NULL )
while( t->left != NULL )
t = t->left;
return t;
}
// Internal method to find the largest item in a subtree t.
// Return node containing the largest item.
template <class Comparable>
BinaryNode<Comparable> * BinarySearchTree<Comparable>::findMax( Node *t ) const
{
if( t != NULL )
while( t->right != NULL )
t = t->right;
return t;
}
// Internal method to find an item in a subtree.
// x is item to search for.
// t is the node that roots the tree.
// Return node containing the matched item.
template <class Comparable>
BinaryNode<Comparable> * BinarySearchTree<Comparable>::
find( const Comparable & x, Node *t ) const
{
//Printouts inserted by gdh for lecture
cout << "BEGIN FIND with = " << t << "( " << t->element << " )" << std::endl;
while( t != NULL ){
if( x < t->element ){
t = t->left;
if (t != NULL){
cout << "CONTINUE FIND with = " << t << " : LEFT ( " << t->element << " )" << std::endl;
}
}
else if( t->element < x ){
t = t->right;
if (t != NULL){
cout << "CONTINUE FIND with = " << t << " : RIGHT ( " << t->element << " )" << std::endl;
}
}
else
return t; // Match
}
return NULL; // Not found
}
// Internal method to make subtree empty.
template <class Comparable>
void BinarySearchTree<Comparable>::makeEmpty( Node * & t ) const
{
if( t != NULL )
{
makeEmpty( t->left );
makeEmpty( t->right );
delete t;
}
t = NULL;
}
// Internal method to clone subtree.
template <class Comparable>
BinaryNode<Comparable> * BinarySearchTree<Comparable>::clone( Node * t ) const
{
if( t == NULL )
return NULL;
else
return new Node( t->element, clone( t->left ), clone( t->right ), t->size );
}
// Returns the kth smallest item in the tree.
// Throws ItemNotFoundException if k is out of range.
template <class Comparable>
Cref<Comparable> BinarySearchTreeWithRank<Comparable>::findKth( int k ) const
{
return elementAt( findKth( k, root ) );
}
// Internal method to insert into a subtree.
// x is the item to insert.
// t is the node that roots the tree.
// Set the new root.
// Throw DuplicateItemException if x is already in t.
template <class Comparable>
void BinarySearchTreeWithRank<Comparable>::
insert( const Comparable & x, Node * & t ) const
{
if( t == NULL )
t = new Node( x, NULL, NULL, 0 );
else if( x < t->element )
insert( x, t->left );
else if( t->element < x )
insert( x, t->right );
else
throw DuplicateItemException( );
t->size++;
}
// Internal method to remove from a subtree.
// x is the item to remove.
// t is the node that roots the tree.
// Set the new root.
// Throw ItemNotFoundException is x is not in t.
template <class Comparable>
void BinarySearchTreeWithRank<Comparable>::
remove( const Comparable & x, Node * & t ) const
{
if( t == NULL )
throw ItemNotFoundException( );
if( x < t->element )
remove( x, t->left );
else if( t->element < x )
remove( x, t->right );
else if( t->left != NULL && t->right != NULL ) // Two children
{
t->element = findMin( t->right )->element;
removeMin( t->right ); // Remove minimum
}
else
{
BinaryNode<Comparable> *oldNode = t;
t = ( t->left != NULL ) ? t->left : t->right; // Reroot t
delete oldNode; // delete old root
return;
}
t->size--;
}
// Internal method to remove minimum item from a subtree.
// t is the node that roots the tree.
// Set the new root.
// Throw UnderflowException if t is empty.
template <class Comparable>
void BinarySearchTreeWithRank<Comparable>::removeMin( Node * & t ) const
{
if( t == NULL )
throw UnderflowException( );
else if( t->left != NULL )
removeMin( t->left );
else
{
Node *tmp = t;
t = t->right;
delete tmp;
return;
}
t->size--;
}
// Internal method to find kth item in a subtree.
// k is the desired rank.
// t is the node that roots the tree.
template <class Comparable>
BinaryNode<Comparable> *
BinarySearchTreeWithRank<Comparable>::findKth( int k, Node * t ) const
{
if( t == NULL )
return NULL;
int leftSize = treeSize( t->left );
if( k <= leftSize )
return findKth( k, t->left );
else if( k == leftSize + 1 )
return t;
else
return findKth( k - leftSize - 1, t->right );
}
The following usage-file bst_usage.cpp is a very simple file only for demonstrations during the lecture (do some exercise: improve it!).
//*******************************+
//
// bst_usage.cpp
//
// -> BinarySearchTree.hpp -> Wrapper.hpp -> Except.hpp , stdlib.h
// -> BinarySearchTree.cpp
//
// author: gerd doeben-henisch
//
//*************************************+
//
// Compilation: g++ -o bstree BinarySearchTree_usage.cpp
// Usage: bstree
//
//******************************************************
#include <iostream>
using namespace std;
#include "BinarySearchTree.hpp"
#include "BinarySearchTree.cpp"
// Test program
int main( )
{
try {
BinarySearchTreeWithRank<int> t;
int NUMS = 0;
int input = 1;
//Adding userinput
while (input > 0 ) {
cout << "Please enter key (End with '0'): ";
cin >>input;
t.insert(input);
if(input > 0) NUMS++;
cout << "ACTUAL NUMBER OF INSERTED VERTICES = " << NUMS << std::endl;
}//end while
//Finding some key
input = 1;
while (input > 0){
cout <<"WHICH KEY SHALL BE SEARCHED (End=0)? : ";
cin >> input;
t.find(input);
if( t.find( input ).get( ) != input )
cout << "Find error0!" << endl;
}//End of while
input=1;
while (input > 0){
if (NUMS < 1){
cout << "no more vertex available !!!" << std::endl;
break;
}
else {
cout <<"WHICH KEY SHALL BE REMOVED (End=0)? : ";
cin >> input;
if( t.find( input ).get( ) != input ) {
cout << "Find error0!" << endl; }
t.remove(input);
NUMS--;
cout << "ACTUAL NUMBER OF INSERTED VERTICES = " << NUMS << std::endl;
}
}//End of while
input = 1;
while (input > 0){
cout <<"WHICH KEY SHALL BE SEARCHED (End=0)? : ";
cin >> input;
t.find(input);
if( t.find( input ).get( ) != input )
cout << "Find error0!" << endl;
}//End of while
}//end try
catch( const DSException & e )
{
cout << e.toString( ) << endl;
}
return 0;
}
The following usgae-file is the original usage-file by WEISS:
//*******************************+
//
// BinarySearchTree_usage.cpp
//
// -> BinarySearchTree.hpp -> Wrapper.hpp -> Except.hpp , stdlib.h
// -> BinarySearchTree.cpp
//
// author: WEISS 2001
// modified for lecture: gerd doeben-henisch
//
//*************************************+
//
// Compilation: g++ -o bstree BinarySearchTree_usage.cpp
// Usage: bstree
//
//******************************************************
#include <iostream>
using namespace std;
#include "BinarySearchTree.hpp"
#include "BinarySearchTree.cpp"
// Test program
int main( )
{
try {
BinarySearchTreeWithRank<int> t;
int NUMS = 40;
const int GAP = 3;
int i, j;
cout << "Checking... (no more output means success)" << endl;
for( i = GAP; i != 0; i = ( i + GAP ) % NUMS )
t.insert( i );
for( i = 1; i < NUMS; i+=2 )
if( t.find( i ).get( ) != i )
cout << "Find error0!" << endl;
for( i = 1; i < NUMS; i+= 2 )
t.remove( i );
if( t.findMin( ).get( ) != 2 || t.findMax( ).get( ) != NUMS - 2 )
cout << "FindMin or FindMax error!" << endl;
for( i = 2; i < NUMS; i+=2 )
if( t.find( i ).get( ) != i )
cout << "Find error1!" << endl;
for( i = 1; i < NUMS; i+=2 )
{
if( !t.find( i ).isNull( ) )
cout << "Find error2!" << endl;
}
BinarySearchTreeWithRank<int> t2;
t2 = t;
for( i = 2; i < NUMS; i+=2 )
if( t2.find( i ).get( ) != i )
cout << "Find error1!" << endl;
for( i = 1; i < NUMS; i+=2 )
{
if( !t2.find( i ).isNull( ) )
cout << "Find error2!" << endl;
}
for( j = 1; j < NUMS / 2 - 1; j++ )
if( t2.findKth( j ).get( ) != j * 2 )
cout << "Findkth error1!" << endl;
}
catch( const DSException & e )
{
cout << e.toString( ) << endl;
}
return 0;
}
The wrapper-class is used here to offer the possibility to connect an object also with a NULL-pointer and providing an exception for the case of an empty object.
//*******************************+
//
// Wrapper.hpp
//
// author: WEISS 2001
// modified for lecture: gerd doeben-henisch
//
// Connected to BinarySearchTree_usage.cpp with BinarySearchTree.hpp
//
//******************************************************
#ifndef WRAPPER_H_
#define WRAPPER_H_
#include <stdlib.h>
#include "Except.hpp"
// Class that wraps a constant reference variable.
// Useful for return value from a container find method.
template <class Object>
class Cref
{
public:
Cref( ) : obj( NULL ) { }
explicit Cref( const Object & x ) : obj( &x ) { }
const Object & get( ) const
{ if( isNull( ) ) throw NullPointerException( ); else return *obj; }
bool isNull( ) const
{ return obj == NULL; }
private:
const Object *obj;
};
#endif
The Except-file defines a specal exception-classes used by WEISS.
//*******************************+
//
// Except.hpp
//
// author: WEISS 2001
// modified for lecture: gerd doeben-henisch
//
// Connected to BinarySearchTree_usage.cpp with BinarySearchTree.hpp
//
//******************************************************
#ifndef EXCEPT_H_
#define EXCEPT_H_
#ifndef NO_RTTI
#include <typeinfo>
#endif
#ifdef SAFE_STL
#include "mystring.h"
#include "StartConv.h"
#else
#include <string>
using namespace std;
#endif
class DSException
{
public:
DSException( const string & msg = "" ) : message( msg )
{ }
virtual ~DSException( )
{ }
virtual string toString( ) const
#ifndef NO_RTTI
{ return "Exception " + string( typeid( *this ).name( ) ) + ": " + what( ); }
#else
{ return "Exception " + string( ": " ) + what( ); }
#endif
virtual string what( ) const
{ return message; }
private:
string message;
};
class GraphException : public DSException
{
public:
GraphException( const string & msg = "" ) : DSException( msg )
{ }
};
class NullPointerException : public DSException
{
public:
NullPointerException( const string & msg = "" ) : DSException( msg )
{ }
};
class IndexOutOfBoundsException : public DSException
{
public:
IndexOutOfBoundsException( const string & msg = "" ) : DSException( msg )
{ }
IndexOutOfBoundsException( int idx, int sz, const string & msg = "" )
: DSException( msg ), index( idx ), size( sz ) { }
int getIndex( ) const
{ return index; }
int getSize( ) const
{ return size; }
private:
int index;
int size;
};
class ArrayIndexOutOfBoundsException : public IndexOutOfBoundsException
{
public:
ArrayIndexOutOfBoundsException( const string & msg = "" )
: IndexOutOfBoundsException ( msg ) { }
ArrayIndexOutOfBoundsException( int idx, int sz, const string & msg = "" )
: IndexOutOfBoundsException( idx, sz, msg ) { }
};
class StringIndexOutOfBoundsException : public IndexOutOfBoundsException
{
public:
StringIndexOutOfBoundsException( const string & msg = "" )
: IndexOutOfBoundsException ( msg ) { }
StringIndexOutOfBoundsException( int idx, int sz, const string & msg = "" )
: IndexOutOfBoundsException( idx, sz, msg ) { }
};
class UnderflowException : public DSException
{
public:
UnderflowException( const string & msg = "" ) : DSException( msg )
{ }
};
class OverflowException : public DSException
{
public:
OverflowException( const string & msg = "" ) : DSException( msg )
{ }
};
class ItemNotFoundException : public DSException
{
public:
ItemNotFoundException( const string & msg = "" ) : DSException( msg )
{ }
};
class DuplicateItemException : public DSException
{
public:
DuplicateItemException( const string & msg = "" ) : DSException( msg )
{ }
};
class IteratorException : public DSException
{
public:
IteratorException( const string & msg = "" ) : DSException( msg )
{ }
};
class IteratorOutOfBoundsException : public IteratorException
{
public:
IteratorOutOfBoundsException( const string & msg = "" ) : IteratorException( msg )
{ }
};
class IteratorUninitializedException : public IteratorException
{
public:
IteratorUninitializedException( const string & msg = "" ) : IteratorException( msg )
{ }
};
class IteratorMismatchException : public IteratorException
{
public:
IteratorMismatchException( const string & msg = "" ) : IteratorException( msg )
{ }
};
class BadArgumentException : public DSException
{
public:
BadArgumentException( const string & msg = "" ) : DSException( msg )
{ }
};
#ifdef SAFE_STL
#include "EndConv.h"
#endif
#endif
Worst case depth of the tree: O(N)
Balanced depth of the tree: O(N * log N)
Internal path length of a binary tree t = the sum of the depth of its vertices.
Average internal path-length: O(1.38 * N * log N)
Average running time with random insert/remove-operations approximately O(log N)
Average depth of a binary tree with random insert/remove-operations approximately O(sqrt(N))
From this it follows that the input to a binary search tree should be rather random than ordered; ordered input drives the shape of a binary search tree to become more and more an ordered sequence having depth O(N).
According to [WEISS 2001:685] are AA-Trees compared to Red-Black-Trees a competitive form of a balanced search tree, but with considerable simpler routines.
As we have seen in the last lecture are binary search trees a useful tool to store ordered information and to retrieve such information in a straightforward way. The only problem is the fact that the order of the incoming information to be stored can in the worst case turn a binary search tree into a mere list. In this worst case search can eventually consume O(N) time untill it is succesful. If one wants to exclude this worst case from becoming real one has to guarantee that a certain balancing condition is kept all the time during the operation of the binary search tree.
How is such a balancing condition defined? There are several strategies in the literature known to be used to represent balanced binary trees. The key idea is to assume, that every path p in a tree t from the root to a leaf has a certain length +/- n. In the ideal case we would have n == 0, thus every path would have the same length. Thus we would have the strong balancing condition with n==0.
But a definition of a balanced BST with the claim that every path should have the same length would be too strong! Consider the following case: t is a BST which fullfills the strong balancing condition with n==0. Now we have to insert a new node n with a ney key k which is not yet part of the graph. This node will be attached at the bottom of the tree t as a child of a leaf, left or right depending from the key.
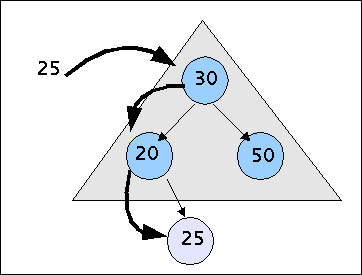
Inserting a new node in a strongly balanced BST
As you can directly see, would any insertion be a violation of thr strong balancing condition; thus we have to weaken this condition. Let us call a more relaxed balancing condition the weakly balancing condition of grade n and let us assume, that we have n==1. With this condition we can insert as many new nodes at the bottom of a tree t as we want.
But the point is that after a finite set of insertions --we will exclude for a moment the case of removing nodes in between insertion operations-- there will inevitably arise the case that we have to insert a new node n' at the end of a path wich has already the lenght n+1 and there is at least one path left with length n. In that case the weakly balancing condition of degree n==1 would be broken.
Because this case of an ever expanding tree t cannot be excluded and at the same time it makes no sense to weaken the balancing condition beyond n==1 one has to ask for a solution, which can handle the case of an expanding path in a way that the balancing condition will be kept valid 'all the time'.
This task is the driving force for the development of different algorithms to enable balancing BSTs. The key-idea of every algorithm for balancing BSTs is to combine the insert- and remove-operations with some additional operations which are watching the balancing condition and, if the balancing condition will become violated, they will remedy this problem.
The general idea of remedy the problem is to shorten the path in which the insertion of a new node has increased the length too much. How to cope with this problem is rather different. In what follows we will have a look (i) to the manner, how the insert- and remove operation of the AATree-algorithm is solving the problem and (ii) we have to prove that this concrete solution is guaranteeing the wanted balancing condition also in the general case.
We start the investigation with the insertion operation of the AATree-algorithm how it is presented to us by WEISS.
The AATree-algorithm assumes that every node has an additional label called level which can represent information about the height of a node above the bottom. Every nullNode below the leaves has level L=0. Every leave gets the value L=1. The only case when the AATree-algorithm increments the level of a node is the positiv completion of a skip-operation. Thus it can happen that on the same path more than one node from bottom upwards can have L=1 and more than one node above those with level L=n can have the level L=n+1.
The AAT-insertion assumes two main cases where the first case has two subcases.
Case 1 is represented by the skew-operation and case 2 by the skip-operation.
The skew-operation is taken as input a node t and the left child x of t if both have the same level-value and changes the order of these both nodes in the manner that x is moved upwards and the node t is becoming the right child of x. The diagramms below show the both subcases:
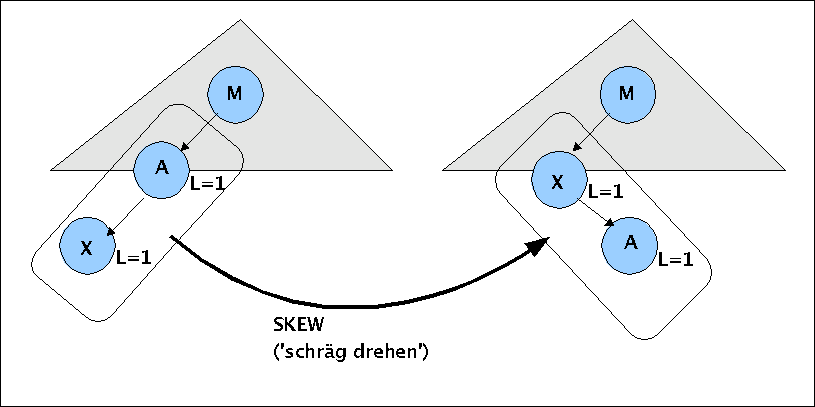
Case 1: skewing a new node in an AATree at the bottom as left node
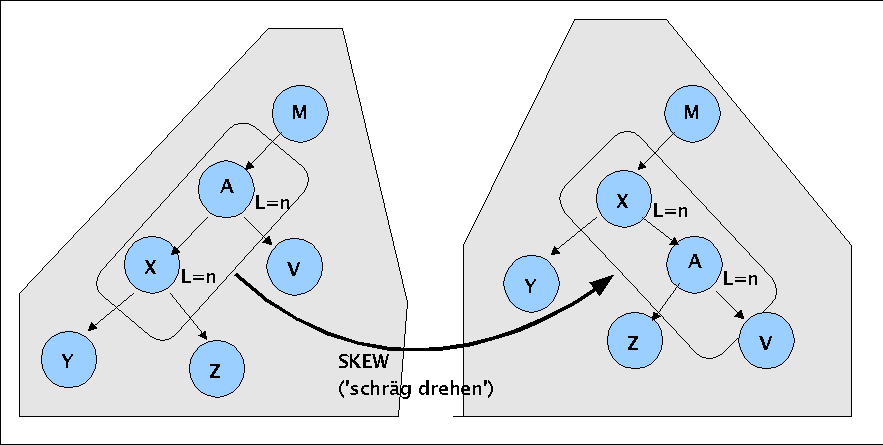
Case 2: Skewing two nodes already inside of a tree
As mentioned before does skewing not change the level of a node; it only rearranges the position of nodes in a way that left childs are made to parents and parents to right childs. By this operation will one path become shortened and another eventually enlarged.
Therefore one has to ask when and where can happen the increasement of a level? And additionally: what happens with nodes inserted as right childs, not as left ones as in the case of the skewing-operation?
At this point comes the other operation into play, the slit-operation.
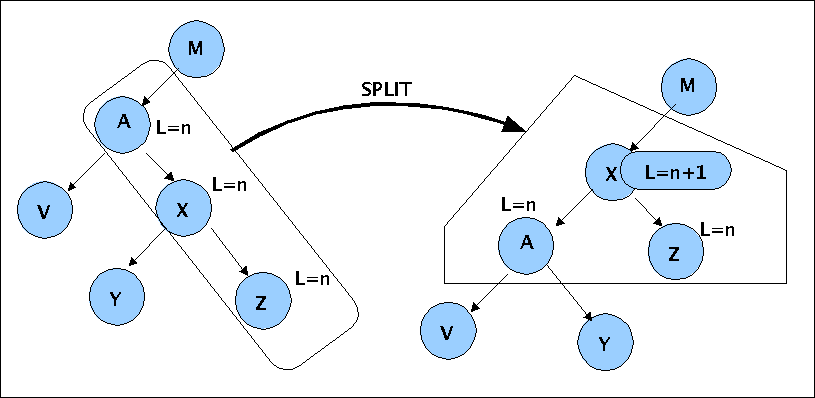
Case 3: splitting three nodes with same level at parent and second right child already inside of a tree
This operation brings one node up and only in this case the level is incremented by one. This operation shortens the path to the right and enlarges a path to the left.
Now one should take a look to the algorithm directly. Below you will also find protocols of examples processed by the algorithm.
The following algorithms are mainly taken from the public sources of [WEISS 2001]; they are modified for educational purposes to demonstrate the behavior during a lecture. The simple usage-file is not from WEISS.
//*********************************
//
// AATree.hpp
//
// --> Wrapper.hpp, Except.hpp, stdlib.h
//
// author: WEIS 2001
// modified for lecture: gerd doeben-henisch
//
//********************************************************
#include "Except.hpp"
#include "Wrapper.hpp"
#include <stdlib.h> // For NULL
// AATree class
//
// CONSTRUCTION: with no parameter or another AA-tree
//
// ******************PUBLIC OPERATIONS*********************
// void insert( x ) --> Insert x
// void remove( x ) --> Remove x
// Comparable find( x ) --> Return item that matches x
// Comparable findMin( ) --> Return smallest item
// Comparable findMax( ) --> Return largest item
// bool isEmpty( ) --> Return true if empty; else false
// void makeEmpty( ) --> Remove all items
// void printPreOrder( ) --> Print nodes in preorder
// ******************ERRORS********************************
// Throws exceptions as warranted
template <class Comparable>
class AATree;
template <class Comparable>
class AANode
{
public:
Comparable element;
AANode *left;
AANode *right;
int level;
AANode( ) : left( NULL ), right( NULL ), level( 1 ) { }
AANode( const Comparable & e, AANode *lt, AANode *rt, int lv = 1 )
: element( e ), left( lt ), right( rt ), level( lv ) { }
public:
void printPreOrder( ) const;
friend class AATree<Comparable>;
};
template <class Comparable>
class AATree
{
public:
AATree( );
AATree( const AATree & rhs );
~AATree( );
Cref<Comparable> findMin( ) const;
Cref<Comparable> findMax( ) const;
Cref<Comparable> find( const Comparable & x ) const;
bool isEmpty( ) const;
void makeEmpty( );
void insert( const Comparable & x );
void remove( const Comparable & x );
const AATree & operator=( const AATree & rhs );
// Recursive traversals, with printing
void printPreOrder( ) const
{ if( root != NULL ) root->printPreOrder( ); }
typedef AANode<Comparable> Node;
private:
Node *root;
Node *nullNode;
Cref<Comparable> elementAt( Node *t ) const;
// Recursive routines
void insert( const Comparable & x, Node * & t );
void remove( const Comparable & x, Node * & t );
void makeEmpty( Node * & t );
// Rotations
void skew( Node * & t ) const;
void split( Node * & t ) const;
void rotateWithLeftChild( Node * & t ) const;
void rotateWithRightChild( Node * & t ) const;
AANode<Comparable> * clone( Node * t ) const;
};
//*********************************
//
// AATree.cpp
//
// --> AATree.hpp --> Wrapper.hpp, Except.hpp, stdlib.h
//
// author: WEIS 2001
// modified for lecture: gerd doeben-henisch
//
//
//********************************************************
// Construct the tree.
template <class Comparable>
AATree<Comparable>::AATree( )
{
nullNode = new Node;
nullNode->left = nullNode->right = nullNode;
nullNode->level = 0;
root = nullNode;
}
// Copy constructor.
template <class Comparable>
AATree<Comparable>::AATree( const AATree<Comparable> & rhs )
{
nullNode = new Node;
nullNode->left = nullNode->right = nullNode;
nullNode->level = 0;
root = clone( rhs.root );
}
// Destructor for the tree.
template <class Comparable>
AATree<Comparable>::~AATree( )
{
makeEmpty( );
delete nullNode;
}
// Insert x into the tree.
// Throws DuplicateItemException if x is already there.
template <class Comparable>
void AATree<Comparable>::insert( const Comparable & x )
{
insert( x, root );
}
// Remove x from the tree.
// Throws ItemNotFoundException if x is not in the tree.
template <class Comparable>
void AATree<Comparable>::remove( const Comparable & x )
{
remove( x, root );
}
//******************************************************************************
// Print the tree rooted at current node using preorder traversal.
template <class Comparable>
void AANode<Comparable>::printPreOrder( ) const
{
cout << this << " WITH " << element << " LEVEL = " << level << endl; // Node
if( left->level != 0 ) {
cout << "LEFT = " << left->element << " FROM " << element << endl;
left->printPreOrder( ); // Left
}
if( right->level != 0 ) {
cout << "RIGHT = " << right->element << " FROM " << element << endl;
right->printPreOrder( ); // Right
}
}
// Return the smallest item in the tree wrapped in a Cref object.
template <class Comparable>
Cref<Comparable> AATree<Comparable>::findMin( ) const
{
if( isEmpty( ) )
return elementAt( NULL );
Node *ptr = root;
while( ptr->left != nullNode )
ptr = ptr->left;
return elementAt( ptr );
}
// Return the largest item in the tree wrapped in a Cref object.
template <class Comparable>
Cref<Comparable> AATree<Comparable>::findMax( ) const
{
if( isEmpty( ) )
return elementAt( NULL );
Node *ptr = root;
while( ptr->right != nullNode )
ptr = ptr->right;
return elementAt( ptr );
}
// Find item x in the tree.
// Return the matching item wrapped in a Cref object.
template <class Comparable>
Cref<Comparable> AATree<Comparable>::find( const Comparable & x ) const
{
Node *current = root;
nullNode->element = x;
for( ; ; )
{
if( x < current->element )
current = current->left;
else if( current->element < x )
current = current->right;
else if( current != nullNode )
return elementAt( current );
else
return elementAt( NULL );
}
}
// Make the tree logically empty.
template <class Comparable>
void AATree<Comparable>::makeEmpty( )
{
makeEmpty( root );
}
// Test if the tree is logically empty.
// Return true if empty, false otherwise.
template <class Comparable>
bool AATree<Comparable>::isEmpty( ) const
{
return root == nullNode;
}
// Deep copy.
template <class Comparable>
const AATree<Comparable> &
AATree<Comparable>::operator=( const AATree<Comparable> & rhs )
{
if( this != &rhs )
{
makeEmpty( );
root = clone( rhs.root );
}
return *this;
}
//**************************************************************************************
// Internal method to wrap the element field in node t inside a Cref object.
template <class Comparable>
Cref<Comparable> AATree<Comparable>::elementAt( Node *t ) const
{
if( t == NULL )
return Cref<Comparable>( );
else
return Cref<Comparable>( t->element );
}
// Internal method to insert into a subtree.
// x is the item to insert.
// t is the node that roots the tree.
// Set the new root.
// Throw DuplicateItemException if x is already in t.
template <class Comparable>
void AATree<Comparable>::
insert( const Comparable & x, Node * & t )
{
cout << "INSERT : Actual Node = " << t << " + Element = " << t->element << std::endl;
if( t == nullNode )
t = new Node( x, nullNode, nullNode );
else if( x < t->element )
insert( x, t->left );
else if( t->element < x )
insert( x, t->right );
else
throw DuplicateItemException( );
cout << "INSERT : Final = " << t << "+ Element = " << t->element << " LEVEL : " << t->level << std::endl;
skew( t );
split( t );
}
// Internal method to remove from a subtree.
// x is the item to remove.
// t is the node that roots the tree.
// Set the new root.
// Throw ItemNotFoundException is x is not in t.
template <class Comparable>
void AATree<Comparable>::
remove( const Comparable & x, Node * & t )
{
static Node *lastNode, *deletedNode = nullNode;
if( t != nullNode )
{
// Step 1: Search down the tree and
// set lastNode and deletedNode
lastNode = t;
if( x < t->element )
remove( x, t->left );
else
{
deletedNode = t;
remove( x, t->right );
}
// Step 2: If at the bottom of the tree and
// x is present, we remove it
if( t == lastNode )
{
if( deletedNode == nullNode || x != deletedNode->element )
throw ItemNotFoundException( );
deletedNode->element = t->element;
deletedNode = nullNode;
t = t->right;
delete lastNode;
}
// Step 3: Otherwise, we are not at the bottom; rebalance
else
if( t->left->level < t->level - 1 ||
t->right->level < t->level - 1 )
{
if( t->right->level > --t->level )
t->right->level = t->level;
skew( t );
skew( t->right );
skew( t->right->right );
split( t );
split( t->right );
}
}
}
// Internal method to make subtree empty.
template <class Comparable>
void AATree<Comparable>::makeEmpty( AANode<Comparable> * & t )
{
if( t != nullNode )
{
makeEmpty( t->left );
makeEmpty( t->right );
delete t;
}
t = nullNode;
}
// Rotate binary tree node with left child.
template <class Comparable>
void AATree<Comparable>::rotateWithLeftChild( Node * & k2 ) const
{
cout << " INSIDE ROTATE WLC " << std::endl;
Node *k1 = k2->left;
cout << " TARGET : " << k2->left->element << " TO BE MOVED UP " << std::endl;
k2->left = k1->right;
cout << " FROM RIGHT TO LEFT : " << k1->right->element << std::endl;
k1->right = k2;
cout << " FROM TOP TO DOWN : " << k2->element << std::endl;
k2 = k1;
cout << " FROM BOTTOM TO TOP : " << k1->element << std::endl;
}
// Rotate binary tree node with right child.
template <class Comparable>
void AATree<Comparable>::rotateWithRightChild( Node * & k1 ) const
{
cout << " INSIDE WRC " << std::endl;
Node *k2 = k1->right;
cout << " TARGET : " << k1->right->element << " TO BE MOVED UP "<< std::endl;
k1->right = k2->left;
cout << " FROM LEFT TO RIGHT : " << k2->left->element << std::endl;
k2->left = k1;
cout << " FROM TOP TO LEFT : " << k1->element << std::endl;
k1 = k2;
cout << " FROM MIDDLE TO TOP : " << k2->element << std::endl;
}
// Skew primitive for AA-trees.
// t is the node that roots the tree.
template <class Comparable>
void AATree<Comparable>::skew( Node * & t ) const
{
cout << "SKEW : Lchild-Level = " << t->left->level << " Parent-Level = " << t->level << std::endl;
if( t->left->level == t->level ) {
cout << "START ROTATE wlc " << std::endl;
rotateWithLeftChild( t );
}
}
// Split primitive for AA-trees.
// t is the node that roots the tree.
template <class Comparable>
void AATree<Comparable>::split( Node * & t ) const
{
cout << "SPLIT : RRchild-Level = " << t->right->right->level << " Parent-Level = " << t->level << std::endl;
if( t->right->right->level == t->level )
{
cout << "START ROTATE wrc " << std::endl;
rotateWithRightChild( t );
t->level++;
cout << "UPDATE LEVEL : " << t->element << " WITH " << t->level << std::endl;
}
}
// Internal method to clone subtree.
template <class Comparable>
AANode<Comparable> *
AATree<Comparable>::clone( Node * t ) const
{
if( t == t->left ) // Cannot test against nullNode!!!
return nullNode;
else
return new Node( t->element, clone( t->left ),
clone( t->right ), t->level );
}
//*******************************+
//
// AATreey_usage.cpp
//
// -> AATree.hpp -> Wrapper.hpp -> Except.hpp , stdlib.h
// -> AATree.cpp
//
// author: gerd doeben-henisch
//
//*************************************+
//
// Compilation: g++ -o aatree AATree_usage.cpp
// Usage: aatree
//
//******************************************************
#include <iostream>
using namespace std;
#include "AATree.hpp"
#include "AATree.cpp"
// Test program
int main( )
{
try {
AATree<int> t;
int NUMS = 0;
int input = 1;
//Adding userinput
while (input > 0 ) {
cout << "--------------------------------------------------------------" << std::endl;
cout << "Please enter key (End with '0'): ";
cin >>input;
t.insert(input);
if(input > 0) NUMS++;
cout << "ACTUAL NUMBER OF INSERTED VERTICES = " << NUMS << std::endl;
cout << "PREORDER - PRINTING" << std::endl;
t.printPreOrder();
}//end while
//Finding some key
input = 1;
while (input > 0){
cout << "--------------------------------------------------------------" << std::endl;
cout <<"WHICH KEY SHALL BE SEARCHED (End=0)? : ";
cin >> input;
t.find(input);
if( t.find( input ).get( ) != input )
cout << "Find error0!" << endl;
}//End of while
input=1;
while (input > 0){
if (NUMS < 1){
cout << "no more vertex available !!!" << std::endl;
break;
}
else {
cout << "--------------------------------------------------------------" << std::endl;
cout <<"WHICH KEY SHALL BE REMOVED (End=0)? : ";
cin >> input;
if( t.find( input ).get( ) != input ) {
cout << "Find error0!" << endl; }
t.remove(input);
NUMS--;
cout << "ACTUAL NUMBER OF INSERTED VERTICES = " << NUMS << std::endl;
cout << "PREORDER - PRINTING" << std::endl;
t.printPreOrder();
}
}//End of while
input = 1;
while (input > 0){
cout <<"WHICH KEY SHALL BE SEARCHED (End=0)? : ";
cin >> input;
t.find(input);
if( t.find( input ).get( ) != input )
cout << "Find error0!" << endl;
}//End of while
}//end try
catch( const DSException & e )
{
cout << e.toString( ) << endl;
}
return 0;
}
//**************************+ // // test1.txt // // testlauf mit aatree // // 12.Juni 2003 // gdh // //******************************** gerd@goedel:~/WEB-MATERIAL/fh/I-ALGO/I-ALGO-EX/EX8+9/AATREE> ./aatree -------------------------------------------------------------- Please enter key (End with '0'): 50 INSERT : Actual Node = 0x80502d0 + Element = 0 INSERT : Final = 0x80502e8+ Element = 50 LEVEL : 1 SKEW : Lchild-Level = 0 Parent-Level = 1 SPLIT : RRchild-Level = 0 Parent-Level = 1 ACTUAL NUMBER OF INSERTED VERTICES = 1 PREORDER - PRINTING 0x80502e8 WITH 50 LEVEL = 1 -------------------------------------------------------------- Please enter key (End with '0'): 30 INSERT : Actual Node = 0x80502e8 + Element = 50 INSERT : Actual Node = 0x80502d0 + Element = 0 INSERT : Final = 0x8050300+ Element = 30 LEVEL : 1 SKEW : Lchild-Level = 0 Parent-Level = 1 SPLIT : RRchild-Level = 0 Parent-Level = 1 INSERT : Final = 0x80502e8+ Element = 50 LEVEL : 1 SKEW : Lchild-Level = 1 Parent-Level = 1 START ROTATE wlc INSIDE ROTATE WLC TARGET : 30 TO BE MOVED UP FROM RIGHT TO LEFT : 0 FROM TOP TO DOWN : 50 FROM BOTTOM TO TOP : 30 SPLIT : RRchild-Level = 0 Parent-Level = 1 ACTUAL NUMBER OF INSERTED VERTICES = 2 PREORDER - PRINTING 0x8050300 WITH 30 LEVEL = 1 RIGHT = 50 FROM 30 0x80502e8 WITH 50 LEVEL = 1 -------------------------------------------------------------- Please enter key (End with '0'): 20 INSERT : Actual Node = 0x8050300 + Element = 30 INSERT : Actual Node = 0x80502d0 + Element = 0 INSERT : Final = 0x8050318+ Element = 20 LEVEL : 1 SKEW : Lchild-Level = 0 Parent-Level = 1 SPLIT : RRchild-Level = 0 Parent-Level = 1 INSERT : Final = 0x8050300+ Element = 30 LEVEL : 1 SKEW : Lchild-Level = 1 Parent-Level = 1 START ROTATE wlc INSIDE ROTATE WLC TARGET : 20 TO BE MOVED UP FROM RIGHT TO LEFT : 0 FROM TOP TO DOWN : 30 FROM BOTTOM TO TOP : 20 SPLIT : RRchild-Level = 1 Parent-Level = 1 START ROTATE wrc INSIDE WRC TARGET : 30 TO BE MOVED UP FROM LEFT TO RIGHT : 0 FROM TOP TO LEFT : 20 FROM MIDDLE TO TOP : 30 UPDATE LEVEL : 30 WITH 2 ACTUAL NUMBER OF INSERTED VERTICES = 3 PREORDER - PRINTING 0x8050300 WITH 30 LEVEL = 2 LEFT = 20 FROM 30 0x8050318 WITH 20 LEVEL = 1 RIGHT = 50 FROM 30 0x80502e8 WITH 50 LEVEL = 1 -------------------------------------------------------------- Please enter key (End with '0'): 80 INSERT : Actual Node = 0x8050300 + Element = 30 INSERT : Actual Node = 0x80502e8 + Element = 50 INSERT : Actual Node = 0x80502d0 + Element = 0 INSERT : Final = 0x8050330+ Element = 80 LEVEL : 1 SKEW : Lchild-Level = 0 Parent-Level = 1 SPLIT : RRchild-Level = 0 Parent-Level = 1 INSERT : Final = 0x80502e8+ Element = 50 LEVEL : 1 SKEW : Lchild-Level = 0 Parent-Level = 1 SPLIT : RRchild-Level = 0 Parent-Level = 1 INSERT : Final = 0x8050300+ Element = 30 LEVEL : 2 SKEW : Lchild-Level = 1 Parent-Level = 2 SPLIT : RRchild-Level = 1 Parent-Level = 2 ACTUAL NUMBER OF INSERTED VERTICES = 4 PREORDER - PRINTING 0x8050300 WITH 30 LEVEL = 2 LEFT = 20 FROM 30 0x8050318 WITH 20 LEVEL = 1 RIGHT = 50 FROM 30 0x80502e8 WITH 50 LEVEL = 1 RIGHT = 80 FROM 50 0x8050330 WITH 80 LEVEL = 1 -------------------------------------------------------------- Please enter key (End with '0'): 60 INSERT : Actual Node = 0x8050300 + Element = 30 INSERT : Actual Node = 0x80502e8 + Element = 50 INSERT : Actual Node = 0x8050330 + Element = 80 INSERT : Actual Node = 0x80502d0 + Element = 0 INSERT : Final = 0x8050348+ Element = 60 LEVEL : 1 SKEW : Lchild-Level = 0 Parent-Level = 1 SPLIT : RRchild-Level = 0 Parent-Level = 1 INSERT : Final = 0x8050330+ Element = 80 LEVEL : 1 SKEW : Lchild-Level = 1 Parent-Level = 1 START ROTATE wlc INSIDE ROTATE WLC TARGET : 60 TO BE MOVED UP FROM RIGHT TO LEFT : 0 FROM TOP TO DOWN : 80 FROM BOTTOM TO TOP : 60 SPLIT : RRchild-Level = 0 Parent-Level = 1 INSERT : Final = 0x80502e8+ Element = 50 LEVEL : 1 SKEW : Lchild-Level = 0 Parent-Level = 1 SPLIT : RRchild-Level = 1 Parent-Level = 1 START ROTATE wrc INSIDE WRC TARGET : 60 TO BE MOVED UP FROM LEFT TO RIGHT : 0 FROM TOP TO LEFT : 50 FROM MIDDLE TO TOP : 60 UPDATE LEVEL : 60 WITH 2 INSERT : Final = 0x8050300+ Element = 30 LEVEL : 2 SKEW : Lchild-Level = 1 Parent-Level = 2 SPLIT : RRchild-Level = 1 Parent-Level = 2 ACTUAL NUMBER OF INSERTED VERTICES = 5 PREORDER - PRINTING 0x8050300 WITH 30 LEVEL = 2 LEFT = 20 FROM 30 0x8050318 WITH 20 LEVEL = 1 RIGHT = 60 FROM 30 0x8050348 WITH 60 LEVEL = 2 LEFT = 50 FROM 60 0x80502e8 WITH 50 LEVEL = 1 RIGHT = 80 FROM 60 0x8050330 WITH 80 LEVEL = 1 -------------------------------------------------------------- Please enter key (End with '0'): 15 INSERT : Actual Node = 0x8050300 + Element = 30 INSERT : Actual Node = 0x8050318 + Element = 20 INSERT : Actual Node = 0x80502d0 + Element = 0 INSERT : Final = 0x8050360+ Element = 15 LEVEL : 1 SKEW : Lchild-Level = 0 Parent-Level = 1 SPLIT : RRchild-Level = 0 Parent-Level = 1 INSERT : Final = 0x8050318+ Element = 20 LEVEL : 1 SKEW : Lchild-Level = 1 Parent-Level = 1 START ROTATE wlc INSIDE ROTATE WLC TARGET : 15 TO BE MOVED UP FROM RIGHT TO LEFT : 0 FROM TOP TO DOWN : 20 FROM BOTTOM TO TOP : 15 SPLIT : RRchild-Level = 0 Parent-Level = 1 INSERT : Final = 0x8050300+ Element = 30 LEVEL : 2 SKEW : Lchild-Level = 1 Parent-Level = 2 SPLIT : RRchild-Level = 1 Parent-Level = 2 ACTUAL NUMBER OF INSERTED VERTICES = 6 PREORDER - PRINTING 0x8050300 WITH 30 LEVEL = 2 LEFT = 15 FROM 30 0x8050360 WITH 15 LEVEL = 1 RIGHT = 20 FROM 15 0x8050318 WITH 20 LEVEL = 1 RIGHT = 60 FROM 30 0x8050348 WITH 60 LEVEL = 2 LEFT = 50 FROM 60 0x80502e8 WITH 50 LEVEL = 1 RIGHT = 80 FROM 60 0x8050330 WITH 80 LEVEL = 1 -------------------------------------------------------------- Please enter key (End with '0'): 10 INSERT : Actual Node = 0x8050300 + Element = 30 INSERT : Actual Node = 0x8050360 + Element = 15 INSERT : Actual Node = 0x80502d0 + Element = 0 INSERT : Final = 0x8050378+ Element = 10 LEVEL : 1 SKEW : Lchild-Level = 0 Parent-Level = 1 SPLIT : RRchild-Level = 0 Parent-Level = 1 INSERT : Final = 0x8050360+ Element = 15 LEVEL : 1 SKEW : Lchild-Level = 1 Parent-Level = 1 START ROTATE wlc INSIDE ROTATE WLC TARGET : 10 TO BE MOVED UP FROM RIGHT TO LEFT : 0 FROM TOP TO DOWN : 15 FROM BOTTOM TO TOP : 10 SPLIT : RRchild-Level = 1 Parent-Level = 1 START ROTATE wrc INSIDE WRC TARGET : 15 TO BE MOVED UP FROM LEFT TO RIGHT : 0 FROM TOP TO LEFT : 10 FROM MIDDLE TO TOP : 15 UPDATE LEVEL : 15 WITH 2 INSERT : Final = 0x8050300+ Element = 30 LEVEL : 2 SKEW : Lchild-Level = 2 Parent-Level = 2 START ROTATE wlc INSIDE ROTATE WLC TARGET : 15 TO BE MOVED UP FROM RIGHT TO LEFT : 20 FROM TOP TO DOWN : 30 FROM BOTTOM TO TOP : 15 SPLIT : RRchild-Level = 2 Parent-Level = 2 START ROTATE wrc INSIDE WRC TARGET : 30 TO BE MOVED UP FROM LEFT TO RIGHT : 20 FROM TOP TO LEFT : 15 FROM MIDDLE TO TOP : 30 UPDATE LEVEL : 30 WITH 3 ACTUAL NUMBER OF INSERTED VERTICES = 7 PREORDER - PRINTING 0x8050300 WITH 30 LEVEL = 3 LEFT = 15 FROM 30 0x8050360 WITH 15 LEVEL = 2 LEFT = 10 FROM 15 0x8050378 WITH 10 LEVEL = 1 RIGHT = 20 FROM 15 0x8050318 WITH 20 LEVEL = 1 RIGHT = 60 FROM 30 0x8050348 WITH 60 LEVEL = 2 LEFT = 50 FROM 60 0x80502e8 WITH 50 LEVEL = 1 RIGHT = 80 FROM 60 0x8050330 WITH 80 LEVEL = 1 -------------------------------------------------------------- Please enter key (End with '0'): 12 INSERT : Actual Node = 0x8050300 + Element = 30 INSERT : Actual Node = 0x8050360 + Element = 15 INSERT : Actual Node = 0x8050378 + Element = 10 INSERT : Actual Node = 0x80502d0 + Element = 0 INSERT : Final = 0x8050390+ Element = 12 LEVEL : 1 SKEW : Lchild-Level = 0 Parent-Level = 1 SPLIT : RRchild-Level = 0 Parent-Level = 1 INSERT : Final = 0x8050378+ Element = 10 LEVEL : 1 SKEW : Lchild-Level = 0 Parent-Level = 1 SPLIT : RRchild-Level = 0 Parent-Level = 1 INSERT : Final = 0x8050360+ Element = 15 LEVEL : 2 SKEW : Lchild-Level = 1 Parent-Level = 2 SPLIT : RRchild-Level = 0 Parent-Level = 2 INSERT : Final = 0x8050300+ Element = 30 LEVEL : 3 SKEW : Lchild-Level = 2 Parent-Level = 3 SPLIT : RRchild-Level = 1 Parent-Level = 3 ACTUAL NUMBER OF INSERTED VERTICES = 8 PREORDER - PRINTING 0x8050300 WITH 30 LEVEL = 3 LEFT = 15 FROM 30 0x8050360 WITH 15 LEVEL = 2 LEFT = 10 FROM 15 0x8050378 WITH 10 LEVEL = 1 RIGHT = 12 FROM 10 0x8050390 WITH 12 LEVEL = 1 RIGHT = 20 FROM 15 0x8050318 WITH 20 LEVEL = 1 RIGHT = 60 FROM 30 0x8050348 WITH 60 LEVEL = 2 LEFT = 50 FROM 60 0x80502e8 WITH 50 LEVEL = 1 RIGHT = 80 FROM 60 0x8050330 WITH 80 LEVEL = 1 -------------------------------------------------------------- Please enter key (End with '0'): 5 INSERT : Actual Node = 0x8050300 + Element = 30 INSERT : Actual Node = 0x8050360 + Element = 15 INSERT : Actual Node = 0x8050378 + Element = 10 INSERT : Actual Node = 0x80502d0 + Element = 0 INSERT : Final = 0x80503a8+ Element = 5 LEVEL : 1 SKEW : Lchild-Level = 0 Parent-Level = 1 SPLIT : RRchild-Level = 0 Parent-Level = 1 INSERT : Final = 0x8050378+ Element = 10 LEVEL : 1 SKEW : Lchild-Level = 1 Parent-Level = 1 START ROTATE wlc INSIDE ROTATE WLC TARGET : 5 TO BE MOVED UP FROM RIGHT TO LEFT : 0 FROM TOP TO DOWN : 10 FROM BOTTOM TO TOP : 5 SPLIT : RRchild-Level = 1 Parent-Level = 1 START ROTATE wrc INSIDE WRC TARGET : 10 TO BE MOVED UP FROM LEFT TO RIGHT : 0 FROM TOP TO LEFT : 5 FROM MIDDLE TO TOP : 10 UPDATE LEVEL : 10 WITH 2 INSERT : Final = 0x8050360+ Element = 15 LEVEL : 2 SKEW : Lchild-Level = 2 Parent-Level = 2 START ROTATE wlc INSIDE ROTATE WLC TARGET : 10 TO BE MOVED UP FROM RIGHT TO LEFT : 12 FROM TOP TO DOWN : 15 FROM BOTTOM TO TOP : 10 SPLIT : RRchild-Level = 1 Parent-Level = 2 INSERT : Final = 0x8050300+ Element = 30 LEVEL : 3 SKEW : Lchild-Level = 2 Parent-Level = 3 SPLIT : RRchild-Level = 1 Parent-Level = 3 ACTUAL NUMBER OF INSERTED VERTICES = 9 PREORDER - PRINTING 0x8050300 WITH 30 LEVEL = 3 LEFT = 10 FROM 30 0x8050378 WITH 10 LEVEL = 2 LEFT = 5 FROM 10 0x80503a8 WITH 5 LEVEL = 1 RIGHT = 15 FROM 10 0x8050360 WITH 15 LEVEL = 2 LEFT = 12 FROM 15 0x8050390 WITH 12 LEVEL = 1 RIGHT = 20 FROM 15 0x8050318 WITH 20 LEVEL = 1 RIGHT = 60 FROM 30 0x8050348 WITH 60 LEVEL = 2 LEFT = 50 FROM 60 0x80502e8 WITH 50 LEVEL = 1 RIGHT = 80 FROM 60 0x8050330 WITH 80 LEVEL = 1 -------------------------------------------------------------- Please enter key (End with '0'):
The following sequence of insertions has been proposed by students: 50, 30, 20, 80, 60, 75, 77...
Konnten aus zeitlichen Gründen nicht mehr behandelt werden.