Theory - Model
The usage of the concepts 'theory' and 'model' in the literature is very broad and does not allow a unique definition. In this text we will follow the tradition of modern theory of science (cf. e.g. the books of F.Suppe (1979) [372], Bourbaki (1970) [29], Balzer (1982)[14], Balzer et. (1987)[15], Ludwig (1978)[238]).
From this tradition we derive the following general assumptions:
Figure 17.1:
Paradim of an Empirical Theory
|
![\includegraphics[width=4.0in]{Theories_FormalModels_3.5in.eps}](img717.png) |
- OBSERVER, Primary Language: Every kind of description is finally rooted in a 'community of observers' [OBS] which are using a 'primary language'
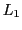 (usually a natural language which has to be presupposed 'as it is'). This primary language
(usually a natural language which has to be presupposed 'as it is'). This primary language 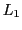 is 'pre-scientific' in the sense that it is not yet a 'theory'. By using the primary language
is 'pre-scientific' in the sense that it is not yet a 'theory'. By using the primary language 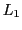 the observers can agree (if possible) in the 'light' of their 'presupposed knowledge'
the observers can agree (if possible) in the 'light' of their 'presupposed knowledge' 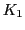 a 'point of view'
a 'point of view' 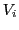 what they want to 'observe' in the 'shared real world'.
what they want to 'observe' in the 'shared real world'.
- MEASUREMENT, Data: If the community of observers [OBS] can define a 'common measurement procedure'
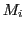 they can start science by making reproducible invariant measurements generating isolated 'data'
they can start science by making reproducible invariant measurements generating isolated 'data' 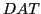 to be written in an 'observer language'
to be written in an 'observer language' 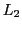 (in many cases the measured events
(in many cases the measured events 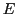 are not perceivable by human persons!). The data expressions from
are not perceivable by human persons!). The data expressions from 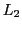 as such have no further meaning then to 'refer' to some 'event' in the 'space of events'
as such have no further meaning then to 'refer' to some 'event' in the 'space of events' 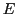 called 'real world'
called 'real world'
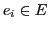 .
.
- DATA, Domains: Depending from the 'view' of the observers one can investigate a manifold of different 'domains' of events. Here, in this text, we will look to (i) 'observable behavior' located in a specified 'environment'; we will correlate this with findings in the area of the 'brain' of animals and humans; (iii) we will correlate this with 'phenomenological knowledge' rooted in the human 'consciousness'. The priority has the observable behavior. We will define a list of experimental environments, which are documented in the literature and which we will use as our 'points of reference'.
- RELATIONS, Expressions To 'explain' the data with regard to some 'forecast' one has to 'construct' a relationship between the data which allows to 'infer' a statement which can be used as a forecast. This can be done by explicitly constructing a 'theory' [TH]. This deserves an additional 'theory language'
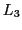 which allows the generation of a set of possible theoretical expressions
which allows the generation of a set of possible theoretical expressions 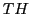 which represent the 'true' sentences of the theory
which represent the 'true' sentences of the theory
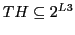 .
.
- INTERPRETATION: To relate a theory expression
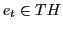 to a measurement expression
to a measurement expression
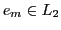 one has to establish a mapping from
one has to establish a mapping from 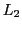 onto a subset
onto a subset 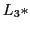 of
of 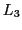 as
as
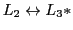 . This mapping works as an 'interpretation' establishing a 'meaning' relation from
. This mapping works as an 'interpretation' establishing a 'meaning' relation from 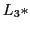 to
to 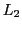 .
.
- LOGIC: To make 'inferences' from expressions of
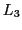 one needs additionally a 'logic' given as a set of 'rules of inference'. It has to be proven that these rules of inference generate only 'true' statements if applied to a set of theoretical expressions which are 'true' (e.g. the axioms of the theory).
one needs additionally a 'logic' given as a set of 'rules of inference'. It has to be proven that these rules of inference generate only 'true' statements if applied to a set of theoretical expressions which are 'true' (e.g. the axioms of the theory).
- THEORY While a 'theory'
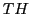 can be understood as a set of expressions of some language
can be understood as a set of expressions of some language 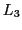 it is common usage in the 'structural approach' to assume as 'basic categories' of the world 'sets'
it is common usage in the 'structural approach' to assume as 'basic categories' of the world 'sets' 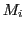 of objects as well as 'relations'
of objects as well as 'relations'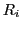 between these. Thus the 'kernel' of a theory is assumed to have the format
between these. Thus the 'kernel' of a theory is assumed to have the format
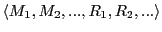 enumerating all assumed basic sets and relations. The relations
enumerating all assumed basic sets and relations. The relations 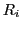 are 'typefied' by applying set operators onto the sets
are 'typefied' by applying set operators onto the sets 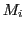 (cf. Bourbaki [29]:chapt.7). Example: having a structure
(cf. Bourbaki [29]:chapt.7). Example: having a structure
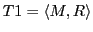 one could typefy the relational term
one could typefy the relational term 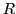 as
as
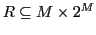 saying that
saying that 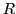 is a relation between the set
is a relation between the set 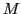 and the power-set of
and the power-set of 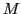 . Including functions as special cases of relations one could construct typefications like
. Including functions as special cases of relations one could construct typefications like
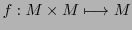 assuming a structure like
assuming a structure like
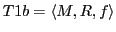 .
.
- COMPLEXITY: The usage of structures allows the introduction of the term 'complexity'. 'Complexity' understood as depending on (i) the number of elements in a structure, (ii) the degree of typification of the relations, as well as (iii) the internal structure of the elements.
- MODEL: A formal theory as a structure describes no concrete 'object in the world'. To use such a structural theory with our investigation we have to construct 'instances'
 of such structures by mapping the abstract sets
of such structures by mapping the abstract sets 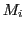 into sets of expressions of
into sets of expressions of 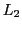 and to map the abstract relations and functions
and to map the abstract relations and functions
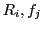 into 'real computing functions' of a 'working theory'
into 'real computing functions' of a 'working theory' 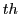 . This can be done e.g. by using a 'programming language' or the language of 'automata' which can further be translated into a program written with a programming language. There can be different models
. This can be done e.g. by using a 'programming language' or the language of 'automata' which can further be translated into a program written with a programming language. There can be different models 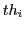 derived from a theory structure
derived from a theory structure 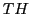
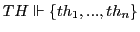 .
.
- VALIDATION: To 'test' the 'validity' of a model
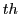 we have to test the possible models against those domains of possible behavior, which are explicitly given in the experimental environments. But, even if a model
we have to test the possible models against those domains of possible behavior, which are explicitly given in the experimental environments. But, even if a model 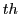 is in 'agreement' with the selected set of an experimental environment, this does not tell us, whether this model
is in 'agreement' with the selected set of an experimental environment, this does not tell us, whether this model 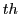 will 'work' in any experimental environment. To validate a model
will 'work' in any experimental environment. To validate a model 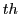 one has to 'expose' the model in the environment and then one has to observe the performance of the model there. This observation has to be specified by defined methods of measurement, which have to be realized as 'automatic protocols' (log-files). The outcome of the measurements should allow at least a comparison between different models in the same environment with regard to the differing properties of the models, giving 'hints' to the implicit properties of the model. This would allow the definition of a relative taxonomy of models. A different kind of evaluation would use experiments which are related to those kinds of experiments, which are used to measure the IQ of children. This would allow an IQ-based taxonomy of models. Other kinds of taxonomy are conceivable.
one has to 'expose' the model in the environment and then one has to observe the performance of the model there. This observation has to be specified by defined methods of measurement, which have to be realized as 'automatic protocols' (log-files). The outcome of the measurements should allow at least a comparison between different models in the same environment with regard to the differing properties of the models, giving 'hints' to the implicit properties of the model. This would allow the definition of a relative taxonomy of models. A different kind of evaluation would use experiments which are related to those kinds of experiments, which are used to measure the IQ of children. This would allow an IQ-based taxonomy of models. Other kinds of taxonomy are conceivable.
Gerd Doeben-Henisch
2013-01-14