Fitness

Accordingly we need a fitness function $fit: P \longmapsto F$ with the above mentioned properties. Goldberg proposed the simple function

$$f = d^{2}$$ (5.11)

$$f \in F$$ (5.12)

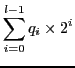$$d = \sum_{i=0}^{l-1}{q_{i} \times 2^{i}}$$ (5.13)

Using our population $Pwork$ from above we can identify the first two elements and translate these binary patterns into decimal numbers with the aid of the scilab function $vec2dec()$ from program GA_v4.sce:

-->element1=Pwork(1,:)
 element1  =
 
    0.    1.    0.    0.    0.  
 
-->l=5,[d]= vec2dec(element1,l)
 l  =
 
    5.  
 d  =
 
    8.  
 
-->element2=Pwork(2,:)
 element2  =
 
    0.    1.    0.    0.    1.  
 
-->l=5,[d]= vec2dec(element2,l)
 l  =
 
    5.  
 d  =
 
    9.

The fitness value $f=d^{2}$ can then easily be computed. With the possible members in the realm of $\langle 0, 0, 0, 0, 0\rangle until \langle 1, 1, 1, 1, 1\rangle$ we have a possible range of fitness values between $[0, ..., 30, 31]$. If we assume as a possible threshold $\theta \geq 30$ then we have as set of selected fitness values $\{31\}$. Then we get as maximal value $upper(F) = 31$. Then we get as possible goal for a genetic process $MAXFIT(P') = \vert P'\vert \times f^{+} = 4 \times 31 = 124$. Thus we will have '124' as '100%'.

One simulation of this population $Pwork$ could then show results (cf. diagram 5.11) where the fitness of the whole population stays below 30% all the time when not using mutation.

Invoking a simulation using the scilab function $gasimple()$ from the program GA_v4.sce:

-->POP=Pwork, l=5,p=5,n=4,run=100,MThreshold=run,[POP,FITNESS_ALLLOG]=gasimple(POP,l,p,n,run, MThreshold)

Figure 5.11: Example Pwork with n=4, l=5, run=100, no mutation