After these preliminary considerations we have to work out a bit more the memory operations. The design shall be guided by the requirements caused by
the overall survival task. Thus we assume the following:
- Important parts of the AC (artificial consciousness) should be stored in the memory M by properties and with transitions
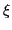 , if
they are new. In case of repetitions the state can become reinforced. Thus every memory element
, if
they are new. In case of repetitions the state can become reinforced. Thus every memory element 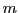 has a
confirmation parameter
has a
confirmation parameter 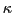 which starts with '1' and can increase by '1'. But there exists some upper bound
which starts with '1' and can increase by '1'. But there exists some upper bound
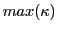 .
.
- Every actual content of the consciousness
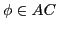 activates a memory element
activates a memory element 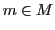 if there exists a certain similarity
between
if there exists a certain similarity
between 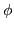 and
and 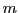 .
.
- If the actual content of the consciousness
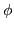 represents an active drive
represents an active drive 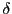 then is the activation of a similar
memory element
then is the activation of a similar
memory element 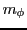 associated with an automatic search for possible 'solutions' given as transitions from the active drive to an
inactive drive. The finding of a solution causes the whole path from active drive state
associated with an automatic search for possible 'solutions' given as transitions from the active drive to an
inactive drive. The finding of a solution causes the whole path from active drive state
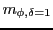 until
until
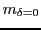 . The next possible state is generated as output
. The next possible state is generated as output 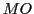 as proposal.
as proposal.
- One can include some kind of forgetting in the manner that after some time period all memory elements
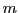 with a
confirmation below a certain threshold
with a
confirmation below a certain threshold
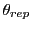 will be deleted.
will be deleted.
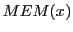 |
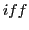 |
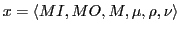 |
(4.118) |
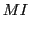 |
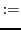 |
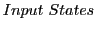 |
(4.119) |
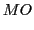 |
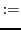 |
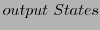 |
(4.120) |
 |
 |
 |
(4.121) |
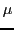 |
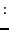 |
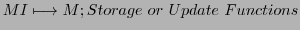 |
(4.122) |
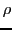 |
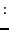 |
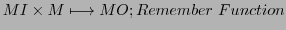 |
(4.123) |
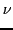 |
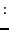 |
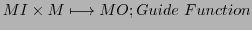 |
(4.124) |
From this follows the following proposal for the format of a memory element 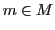 :
:
where
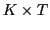 denotes a confirmation coefficient
denotes a confirmation coefficient
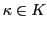 as well as a time stamp
as well as a time stamp 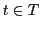 . Associated with the following
translation rule for the storage of the AC:
. Associated with the following
translation rule for the storage of the AC:
In the case of the wood1* scenario one can use the following values:
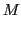 |
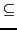 |
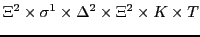 |
(4.127) |
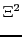 |
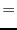 |
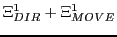 |
(4.128) |
 |
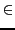 |
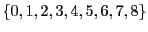 |
(4.129) |
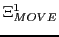 |
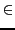 |
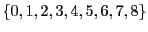 |
(4.130) |
 |
 |
 |
(4.131) |
 |
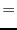 |
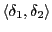 |
(4.132) |
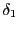 |
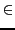 |
 |
(4.133) |
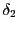 |
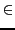 |
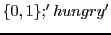 |
(4.134) |
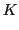 |
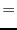 |
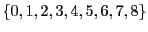 |
(4.135) |
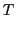 |
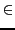 |
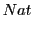 |
(4.136) |
In case of the wood1 scenario with an agent of type 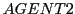 we assume that the agent can differentiate it's output action in a direction
part
we assume that the agent can differentiate it's output action in a direction
part
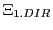 and in a moving part
and in a moving part
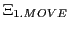 . With this differentiation he can move 'with deliberation'.
. With this differentiation he can move 'with deliberation'.
The protocol of the AC for a certain time window could look like this:
-
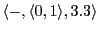 (Empty space, hungry, looking to 3, moving to 3)
(Empty space, hungry, looking to 3, moving to 3)
-
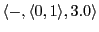 (Empty space, hungry, looking to 3, no move)
(Empty space, hungry, looking to 3, no move)
-
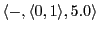 (Empty space, hungry, looking to 5, no move)
(Empty space, hungry, looking to 5, no move)
-
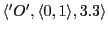 (See an object, hungry, looking to 3, moving to 3)
(See an object, hungry, looking to 3, moving to 3)
-
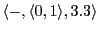 ...
...
-
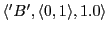
-
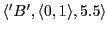
-
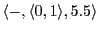
-
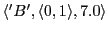
-
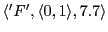
-
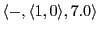 (Empty space, playing around, looking to 7, no move)
(Empty space, playing around, looking to 7, no move)
Then one can map the AC-protocol into the memory as follows:
-
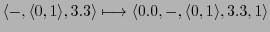
-
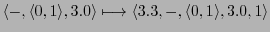
-
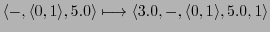
-
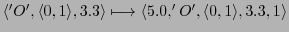
-
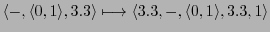
-
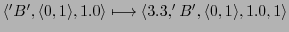
-
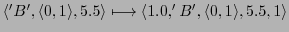
-
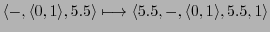
-
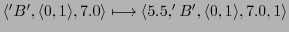
-
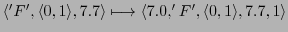
-
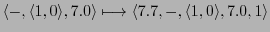
Thus we would get the following memory content:
-
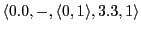 (Causing action '0.0', empty space, hungry, direction 3, move 3, count is 1)
(Causing action '0.0', empty space, hungry, direction 3, move 3, count is 1)
-
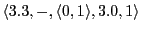 (Causing action '3.3', empty space, hungry, direction 3, move 0, count is 1)
(Causing action '3.3', empty space, hungry, direction 3, move 0, count is 1)
-
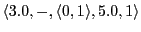 ....
....
-
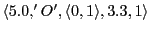
-
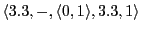
-
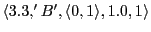
-
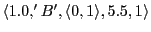
-
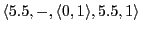
-
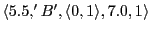
-
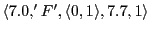
-
Gerd Doeben-Henisch
2012-03-31
![]() :
:
![]() denotes a confirmation coefficient
denotes a confirmation coefficient
![]() as well as a time stamp
as well as a time stamp ![]() . Associated with the following
translation rule for the storage of the AC:
. Associated with the following
translation rule for the storage of the AC:
![]() we assume that the agent can differentiate it's output action in a direction
part
we assume that the agent can differentiate it's output action in a direction
part
![]() and in a moving part
and in a moving part
![]() . With this differentiation he can move 'with deliberation'.
. With this differentiation he can move 'with deliberation'.