Finite Automata and Languages

The concept of automata is closely related to the concept of a language, which can be recognized by an automaton. Another word for recognize is accept. Thus one can characterize an automaton A by the language L which is accepted by that automaton, written as L(A). And according to the hierarchy of automata can one establish a hierarchy of languages corresponding to the automata of the automata hierarchy. The concept of the language hierarchy as chomsky hierarchy is traced back to Chomsky 1956 [53], but the commonly known decription of the 4 levels of language complexity can not be found yet in this paper. There are four other papers mentioned by Mateescu and Salomaa(1997) [193]:p.175, which are also contributing to the development of the final concept of the chomsky hierarchy (cf. [54], [55], [57], and [56]). Hopcroft and Ullmann (1979) give no sources at all (cf. [137]:p.217). (A more detailed analysis of the historical development of the term 'chomsky hierarchy' seems to be necessary!). In an informal way the concept of the chomsky hierarchy is described as follows (cf. Hopcroft and Ullmann (1979)[137]:Pp.216ff):

The Chomsky hierarchy consists of the following levels:

1. Type-0 grammars (also unrestricted or phrase structure grammar or semi-Thue system) include all formal grammars. They generate exactly all languages that can be recognized by a Turing machine. These languages are also known as the recursively enumerable languages. Note that this is different from the recursive languages which can be decided by an always-halting Turing machine. 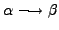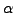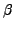The rules are $\alpha \longrightarrow \beta$ with $\alpha$, $\beta$ as arbitrary strings of gramar symbols, but $\alpha \not= \epsilon$.

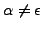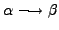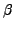2. Type-1 grammars (also context-sensitive grammars) generate the context-sensitive languages. These grammars have rules of the form $\alpha \longrightarrow \beta$ where $\beta$ must at least be as long as 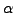$\alpha$. Another format of the grammar rule is in a socalled normalform like 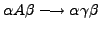$\alpha A\beta \longrightarrow \alpha\gamma\beta$ with A a nonterminal and 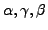$\alpha, \gamma, \beta$ strings of terminals and nonterminals. The strings 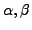$\alpha, \beta$ may be empty, but 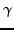$\gamma$ must be nonempty. The languages described by these grammars are exactly all languages that can be recognized by a linear bounded automaton, LBA (a nondeterministic Turing machine whose tape is restricted to the input string and two squares for the endmarkers.)

3. Type-2 grammars (context-free grammars, also often written in the Backus-Naur Form) generate the context-free languages. These are defined by rules of the form 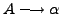$A \longrightarrow \alpha$ with A a nonterminal and 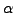$\alpha$ a string of terminals and nonterminals. These languages are exactly all languages that can be recognized by a non-deterministic pushdown automaton, PDA. Context free languages are the theoretical basis for the syntax of most programming languages.

4. Type-3 grammars (regular grammars either as right linear or left linear grammar) generate the regular languages. Such a grammar restricts its rules to a single nonterminal on the left-hand side and a right-hand side consisting of a single terminal B, possibly followed (or preceded, but not both in the same grammar) by a single nonterminal w. The right-linear version is A 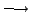$\longrightarrow$ wB or A 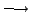$\longrightarrow$ w; the left-linear version is A 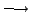$\longrightarrow$ Bw or A 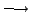$\longrightarrow$ w. These languages are exactly all languages that can be decided by a finite state automaton DFA. Additionally, this family of formal languages can be obtained by regular expressions. Regular languages are commonly used to define search patterns and the lexical structure of programming languages.

Every regular language is context-free, every context-free language is context-sensitive and every context-sensitive language is recursive and every recursive language is recursively enumerable. These are all proper inclusions, meaning that there exist recursively enumerable languages which are not recursive, recursive languages that are not context-sensitive, context-sensitive languages which are not context-free and context-free languages which are not regular.