Next: Beispiel Up: Systembeschreibung Previous: Input-Output Contents
Das System besteht in diesem Beispiel aus einem Netzwerk von Neuronen. Solch ein Netzwerk kann man verstehen als eine mathematische Struktur, die eine Menge von Neuronen ![]() , Gewichten
, Gewichten ![]() sowie Beziehungen
sowie Beziehungen ![]() zwischen diesen Neuronen und Gewichten umfaßt sowie eine Operation
zwischen diesen Neuronen und Gewichten umfaßt sowie eine Operation ![]() über diesen Mengen. Als Formeln:
über diesen Mengen. Als Formeln:
| (10.5) | |||
| (10.6) | |||
| (10.7) |
Dieses Schema soll nun zu einem konkreten Netzwerk spezialisiert (instantiiert) werden, wie es im Bild 10.7 angezeigt wird.
![\includegraphics[width=4.5in]{ann_bsp1.eps}](img223.png) |
Für die Menge der Neuronen ![]() nehmen wir vier Neuronen an, zwei sensorische Neuronen
nehmen wir vier Neuronen an, zwei sensorische Neuronen ![]() und zwei binäre Neuronen
und zwei binäre Neuronen ![]() :
:
| (10.8) |
Dabei soll gelten,
![]() . Diese Neuronen verknüpfen wir mittels der Verknüpfungsrelation
. Diese Neuronen verknüpfen wir mittels der Verknüpfungsrelation ![]() wie folgt:
wie folgt:
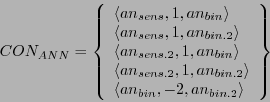
Jetzt fehlt nur noch die dynamische Abarbeitungsfunktion ![]() . Hier lassen sich viele Varianten denken. Ein einfaches Beispiel wird durch den folgenden Algorithmus dargestellt (vgl. die Formel 10.10). Die Grundidee besteht darin, daß die Werte des neuronalen Netzes in diesem Fall von links nach rechts berechnet werden. Liegt ein Ausgangswert vor, wird die Berechnung wieder bei den Eingängen wiederholt. Ein Durchgang entspricht dann einem Zyklus innerhalb eines Prozesses bzw. einer Einheit auf einer abstrakten Zeitlinie.
. Hier lassen sich viele Varianten denken. Ein einfaches Beispiel wird durch den folgenden Algorithmus dargestellt (vgl. die Formel 10.10). Die Grundidee besteht darin, daß die Werte des neuronalen Netzes in diesem Fall von links nach rechts berechnet werden. Liegt ein Ausgangswert vor, wird die Berechnung wieder bei den Eingängen wiederholt. Ein Durchgang entspricht dann einem Zyklus innerhalb eines Prozesses bzw. einer Einheit auf einer abstrakten Zeitlinie.
Die Abarbeitungsfunktion ![]() wird zusammengesetzt aus mehreren Teilfunktionen. Die Teilfunktion
wird zusammengesetzt aus mehreren Teilfunktionen. Die Teilfunktion ![]() beginnt bei den sensorischen Neuronen und bildet daraus eine erste Nachfolgermenge
beginnt bei den sensorischen Neuronen und bildet daraus eine erste Nachfolgermenge ![]() . Für jedes Element der Menge
. Für jedes Element der Menge ![]() wird dann jeweils die Neuronfunktion mit der Teilfunktion
wird dann jeweils die Neuronfunktion mit der Teilfunktion ![]() berechnet. Ausgehend von
berechnet. Ausgehend von ![]() werden mit der Funktion
werden mit der Funktion ![]() wieder alle Nachfolger berechnet, also
wieder alle Nachfolger berechnet, also ![]() und für diese mit
und für diese mit ![]() wieder alle Neuronfunktionen
wieder alle Neuronfunktionen
![]() . Dann wird mit der Teilfunktion
. Dann wird mit der Teilfunktion ![]() geprüft, ob die letzten Neuronen schon berechnet worden sind. Mit der Annahme, daß alle Ausgangsneuronen von den Inputneuronen aus alle die gleiche minimale Pfadlänge haben, kann die Berechnung der Menge
geprüft, ob die letzten Neuronen schon berechnet worden sind. Mit der Annahme, daß alle Ausgangsneuronen von den Inputneuronen aus alle die gleiche minimale Pfadlänge haben, kann die Berechnung der Menge ![]() bei minimaler Pfadlänge
bei minimaler Pfadlänge ![]() dann wieder von vorne beginnen, andernfalls muß sie bei der Teilfunktion
dann wieder von vorne beginnen, andernfalls muß sie bei der Teilfunktion ![]() fortgesetzt werden.
fortgesetzt werden.
Für die Berechnung der einzelnen Neuronen benötigt man die Struktur dieser Neuronen. Für Eingangsneuronen -auch sensorische Neuronen genannt- gilt:
| (10.15) |
Der Aktivierungszustand und der Schwellwert werden hier -stark vereinfachend- als leere Mengen ![]() angenommen, da der Ausgabewert ausschließlich vom Eingabewert abgängen soll:
angenommen, da der Ausgabewert ausschließlich vom Eingabewert abgängen soll:
| (10.16) |
dabei wird angenommen, daß die Neuronfunktion ![]() des sensorischen Neurons im Beispiel eine Identitätsfunktion ist, d.h.
des sensorischen Neurons im Beispiel eine Identitätsfunktion ist, d.h.
| (10.17) |
Im allgemeinen Fall kann die Funktion eines sensorischen Neurons natürlich erheblich komplexer strukturiert sein. Für die beiden binären Neuronen in der Zwischenschicht und in der Ausgangsschicht gelten folgende Zusammenhänge (siehe auch das Beispiel über binäre Neuronen):
| (10.18) | |||
| (10.19) | |||
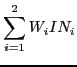 |
(10.20) | ||
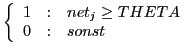 |
(10.21) |
Gerd Doeben-Henisch 2013-01-17