|
|
I-TI04 Theoretische Informatik WS04
|
Wie die historische Darlegung gezeigt hat, konkretisierte sich der Begriff der Berechenbarkeit vornehmlich im Konzept der Turingmaschine und all den davon ableitbaren anderen Automatentypen. Gleichbedeutend damit entwickelte sich sehr bald das Konzept der formalen Grammatik und der zugehörigen formalen Sprachen sowie die Äquivalenzbeziehungen zwischen Grammatiktyp und Automatentyp. Vor diesem geschichtlichen Hintergrund werden wir daher die zentralen Begriffe anhand der Automaten und der Grammatiken einführen und darauf aufbauend dann die Frage der Entscheidbarkeit und der Komplexität diskutieren. Daran sollen sich dann erste Überlegungen zum maschinellen Lernen anschliessen.
Das nachfolgende Schaubild zeigt nochmals im zusammenfassenden Überblick die vier wesentlichen Konzepte, die in der Verbundvorlesung "Theoretische Informatik" einerseits und "Rechnerarchitektur" andererseits erkäutert werden sollen.
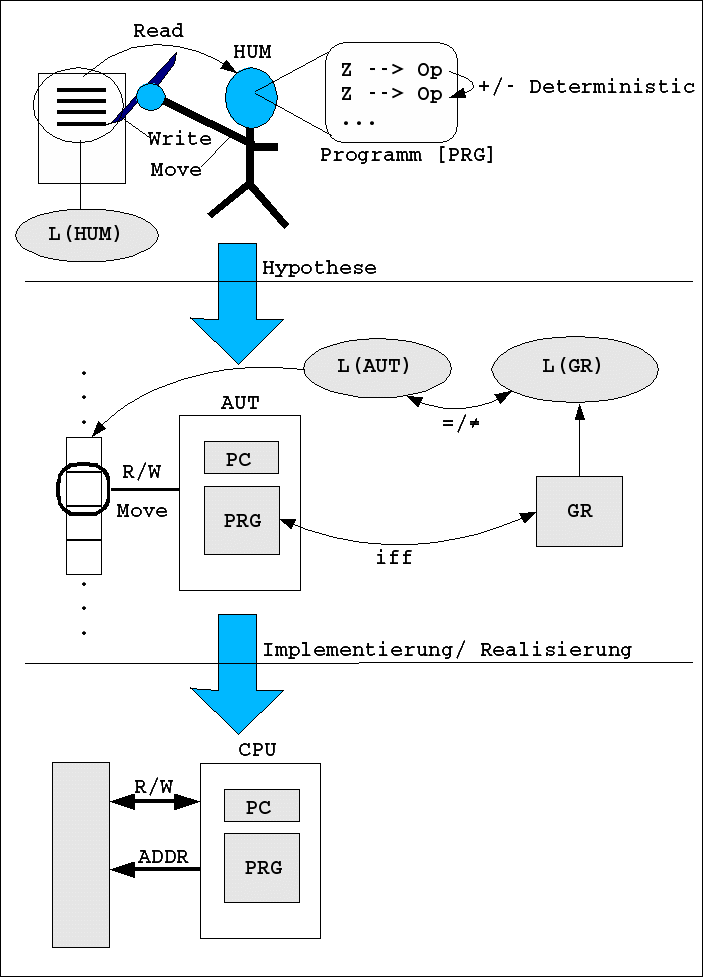
Übersicht
Ausgangspunkt bildet das Verhalten eines Menschen (Human, HUM) der mittels eines Schreibgerätes auf Papier endliche Zeichenketten schreiben (write, W) kann. Schreiben beinhaltet dabei auch Überschreiben bzw. Löschen. Diese Zeichenketten werden aus einem endlichen Zeichenvorrat (Alphabet) genommen. Zugleich kann der Mensch den Inhalt des Blattes auch lesen (read, R). Abstrakt kann unterstellt werden, dass der Mensch intern einer endlichen Liste von Anweisungen folgt (sein "Programm, PRG"), wobei bestimmte Zustände (Z) bestimmte Operationen (Op) implizieren. Der Übergang von einer aktuellen/ aktiven Anweisung zur nächsten Anweisung kann deterministisch oder nicht-deterministisch erfolgen. Zeichenketten, die durch uneigentliche Zeichen von anderen Zeichenketten getrennt sind, sollen Wörter heissen. Die Menge der erlaubten Wörter soll vom Menschen benutzte Sprache heissen (L(HUM)).
Diese vorausgehende Beschreibung eines Menschen beschreibt umgangssprachlich einen Ausschnitt der Realität. Auf der Basis solcher realitätsbezogenen Darstellungen kann man nun versuchen formale Modelle zu konstruieren (Modellierung), die man als mögliche Hypothesen über die Realität auffassen kann.
Drei Beispiele für mögliche Hypothesen seien hier genannt:
Turings Berechenbarkeits-Hypothese (später auch Churchs Hypothese genannt (vgl. [MINSKY 1967:108f], [TURING 1936/7]): Turing nahm an, dass das, was ein Mensch tut, wenn er mit Zeichenketten auf Blättern operiert, letztlich berechenbare Prozesse ("effective procedure") sind und dass sich diese erschöpfend mit Hilfe seines Automaten --später von Church Turingmaschine genannt)-- beschreiben lassen.
Turings Gehirn-Hypothese: ca. 11 Jahre nach der Erfindung der Turingmaschine stellte Turing die Vermutung auf, dass das menschliche Gehirn vermutlich nicht mehr kann als eine Turingmaschine bzw. dass eine Turingmaschine alles kann, was auch ein menschliches Gehirn kann (vgl. [TURING 1948]).
Computational-Semiotics-Hypothese: Aufgrund der beiden vorausgehenden Hypothesen habe ich versucht zu zeigen, dass sich das, was man unter einem menschlichen Zeichenbenutzer im Sinne der Semiotik von Charles Morris versteht, mittels einer Turingmaschine abbilden lässt (vgl. [DÖBEN-HENISCH 1999]).
Wichtig ist hierbei, dass formale Modelle in ihrer Beziehung zur Realität aus erkenntnistheoretischer und wissenschaftstheoretischer Sicht niemals den Status von Beweisen haben, sondern nur von Hypothesen; passende Fakten können die Hypothese bestätigen, unpassende können sie widerlegen; eine endgültige Sicherheit wird man niemals haben da die zu erklärende empirische Realität ein prinzipiell unabgeschlossenes Etwas ist.
Von den vielen möglichen formalen Modellen, die zur Beschreibung (und dann auch partieller Erklärung) konstruiert werden können, wollen wir hier nur zwei betrachten: formale Automaten (AUT) und formale Grammatiken (GR).
Die Grundstruktur eines Automaten ist extrem einfach. Die Papierblätter des menschlichen Schreibers werden hier --im einfachen Fall-- ersetzt durch ein unendliches Band von Kästchen, in denen Zeichen eines endlichen Alphabetes geschrieben werden können. Im maximalen Fall kann der Automat mit einem Schreib-Lese-Kopf sich entlang dem Band bewegen und entweder den Inhalt eines Feldes lesen oder ihn schreiben (umfasst auch Löschen des Inhaltes). Die Steuerung des Lesens/ Schreibens/ Bewegens erfolgt durch ein endliches Programm, desen Anweisungen deterministisch oder nicht-deterministisch erfolgen kann. Der Programmzähler (PC, Program counter) dient nur dazu, die aktuelle Anweisung zu notieren.
Die Menge der Zeichenketten, die ein Automat als "erlaubt" akzeptiert, bilden die vom Automat akzeptierte Sprache (L(AUT)).
Eine formale Grammatik besteht im wesentlichen auch aus einer endlichen Menge von Produktionsregeln, die festlegen, welche Zeichenketten über einem endlichen Alphabet gebildet werden dürfen. Die Menge dieser Zeichenketten bildet die von der Grammatik erzeugbare Sprache (L(GR)).
Da sowohl der formale Automat wie auch die formale Grammatik vollständig formal definiert sind, ist es möglich, die Beziehung zwischen Automaten, Grammatiken und deren Sprachen rein formal zu untersuchen und formale Beweise über deren Eigenschaften zu führen. Zwei Typen von Beweisen sind hier interessant:
L(AUT) = L(GR): Man zeigt, dass die Sprache, die ein bestimmter Automat AUT akzeptiert, äquivalent ist zu der Sprache, die eine Grammtik GR generieren kann.
AUT gdw GR: Man zeigt, dass man zu einem bestimmten Automaten AUT eine bestimmte Grammatik GR konstruieren kann und umgekehrt.
Aufgrund von solchen formalen Beweisen kann man dann allgemeingültige Behauptungen über die Gleichwertigkeit unterschiedlicher formaler Strukturen aufstellen. Dies ist für die Praxis sehr wichtig. Auf diese Weise kann man genau bestimmten, welcher Typ von Automat benötigt wird, um einen bestimmten Typ von formaler Sprache akzeptieren zu können. Dies ist deswegen von Bedeutung, da einfache Sprachen in der Regel "effizient" erkannt werden können, kompliziertere Sprachen aber möglicherweise überhaupt nicht (so gibt es z.B. bis heute keinerlei Automaten, um natürliche Sprachen vollständig zu akzeptieren). Die Klassifikation einer zu akzeptierenden Sprache sowie des zugehörigen Automaten ist daher für die praktische Anwendugn von allgergrösster Bedeutung.
Schliesslich sei an dieser Stelle auch darauf hingewiesen --und dies ist wesentlich Stoff der parallelen Vorlesung "Rechnerarchitektur"-- dass die konkreten Computer, die wir heute kennen, relativ zu den formalen Komzepten zu verstehen sind als partielle Implementierungen/ Realisierungen der formalen Konzepte. Die Beziehung zwischen formalem Konzept und realer Instanz ist keinesfalls die eines "Beweises"! Eine Realisierung eines formalen Konzeptes kann einmal niemals vollständig sein, zum anderen ist es niemals vollständig sicher, ob die konkrete Instanz tatsächlich alle Eigenschaften eines formalen Konzeptes besitzt. Und selbst wenn dies für eine bestimmte Zeitspanne tatsächlich der Fall ist, wird sich dies aufgrund von Materialeigenschaften in der Regel mit der Zeit ändern.
Ein konkreter Computer besitzt statt eines Bandes mit Feldern heute in der Regel Speicherbausteine, die addressierbare Speicherzellen enthalten. Die Bewegung des Schreib-Lese-Kopfes wird durch die Addressierung der Zellen realisiert. Eine addressierte Zelle kann dann gelesen oder geschrieben werden. Parallel zum Speicher findet sich dann in der Regel eine CPU, die im Kern auch ein Programm enthält --den sogenannten Mikrokode--, der das Verhalten der CPU in Abhängigkeit von den gelesenen Daten aus dem Speicher festlegt. In modernen CPUs ist das Verhalten des Mikroprogramms partiell nicht-deterministisch. Ebenfalls findet man auch einen Programmzähler (PC). Zwar hat ein realer Computer immer einen endlichen Speicher gegenüber dem unendlichen Band der formalen Automaten, aber ansonsten kann man zwischen formalem Automaten und realem Computer immer eine vollständige Abbildung herstellen (allerdings immer nur unter dem Vorbehalt, dass die beschreibbaren Eigenschaften eines realen Computers auch "tatsächlich" so gegeben sind).
Wir werden jetzt zunächst die drei wichtigsten Automatentypen im Vergleich betrachten. Im direkten Vergleich deswegen, da damit schon auf den ersten Blick sowohl die Ähnlichkeit wie auch die Verschiedenheit sofort vor Augen tritt. Anschliessend werden wir die Darlegung zu den einzelnen Automaten schrittweise vertiefen, wobei die verfügbare endliche zeit dieser Darlegung Grenzen setzen wird.
Die drei wichtigsten Automaten sind die Turingmaschine [TM], der Push Down Automat [PDA] (auch Kellerautomat genannt mit dem Wort "Keller" für "stack"), sowie der Finite Automat [FA] (auch endlicher Automat genannt).
Die Turingmaschine ist wichtig, da auf ihre nahezu alle wichtigen theoretischen Konstrukte beruhen. Der Push Down Automat und der finite Automat sind wichtig, da diese diejenigen sind, die fast ausschliesslich in der Praxis zum Einsatz kommen.
Das erste Schaubild zeigt die Turingmaschine im direkten Vergleich mit einem Kellerautomaten.
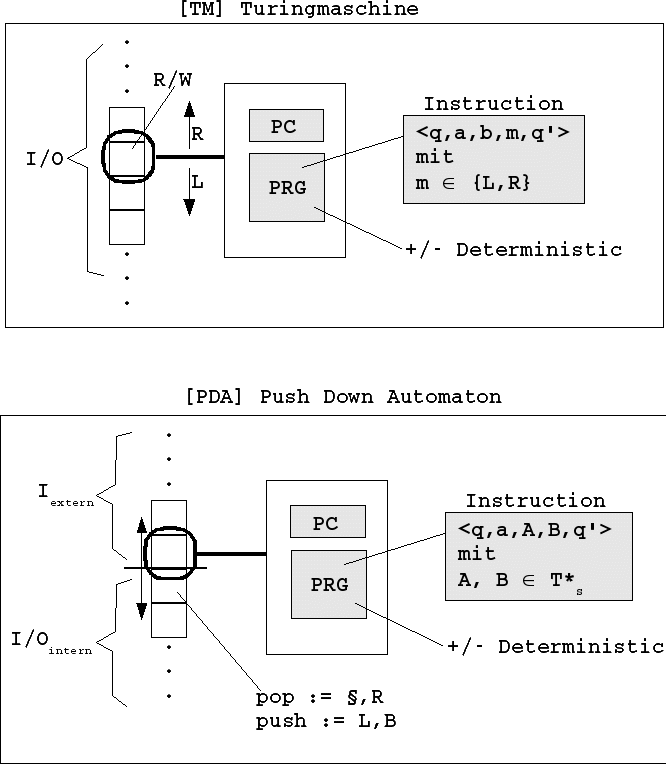
TM und PDA
Die Funktionsweise einer TM lässt sich informell sehr einfach beschreiben. Ihr steht ein unendliches Band zur Verfügung, in deren Felder Zeichen aus einem endlichen Alphabet ALPH geschrieben werden können; dazu gehört auch das leere Zeichen '§'. Mit Hilfe eines Schreib-Lese-Kopfes kann die TM mit Bewegungen nach Links (left) 'L' oder Rechts (right) 'R' jedes einzelne Feld ansteuern. Was eine TM in einem bestmmten Augenblick tut, das hängt davon ab, welcher Befehl (instruction) aus ihrem Programm (PRG) gerade aktiviert ist. Der Programmzähler (PC) enthält immer die ID des aktuellen Befehls. Im Falle einer deterministischen TM (DTM) hat ein solcher Befehl die Form:
<q,a,b,m,q'>
Dabei bedeutet im einzelnen:
q:= der aktuelle Befehl/Zustand
a:= das aktuell gelesene Zeichen
b:= das zu schreibende Zeichen; kann auch Leer '§' sein
m:= die auszuführende Bewegung {L,R,S}; wobei 'S' hier für 'stop' steht, d.h. die Maschine soll anhalten; diese Bwegeung ist allerdings im Gesamtkontext redundant und nur wegen der leichteren Lesbarkeit eingefügt.
q':= der nächste auszuführende Befehl
Im Falle einer nicht-deterministen TM [NTM] kann es mehr als einen Folgebefehl geben, also:
<q,a,b,m,{q'1, ..., q'k}>
Dies bedeutet, dass per Zufall entschieden wird, welcher der endlich vielen Folgebefehle ausgewählt werden soll.
Wie an späterer Stelle zu zeigen ist, ist eine NTM tatsächlich nicht mächtiger als eine DTM! Auch führt die Einführung von zusätzlichen Bändern und Schreib-Lese-Köpfen nicht zu stärkeren Maschinen.
Das Programm einer TM kann man auch als sogenannten Zustandsgraphen schreiben: der aktuelle Zustand q ist dann der Name eines Knoten. Abhängig von den verschiedenen Eingabezeichen gibt es dann verschiedene Pfeile (kanten, edges) die zu anderen Zuständen führen. Die Label an diesen Pfeilen enthalten die Angabe des Zeichens, das geschrieben werden soll sowie die Bewegung, die dann ausgeführt werden soll. Betrachten wir das folgende Beispiel:
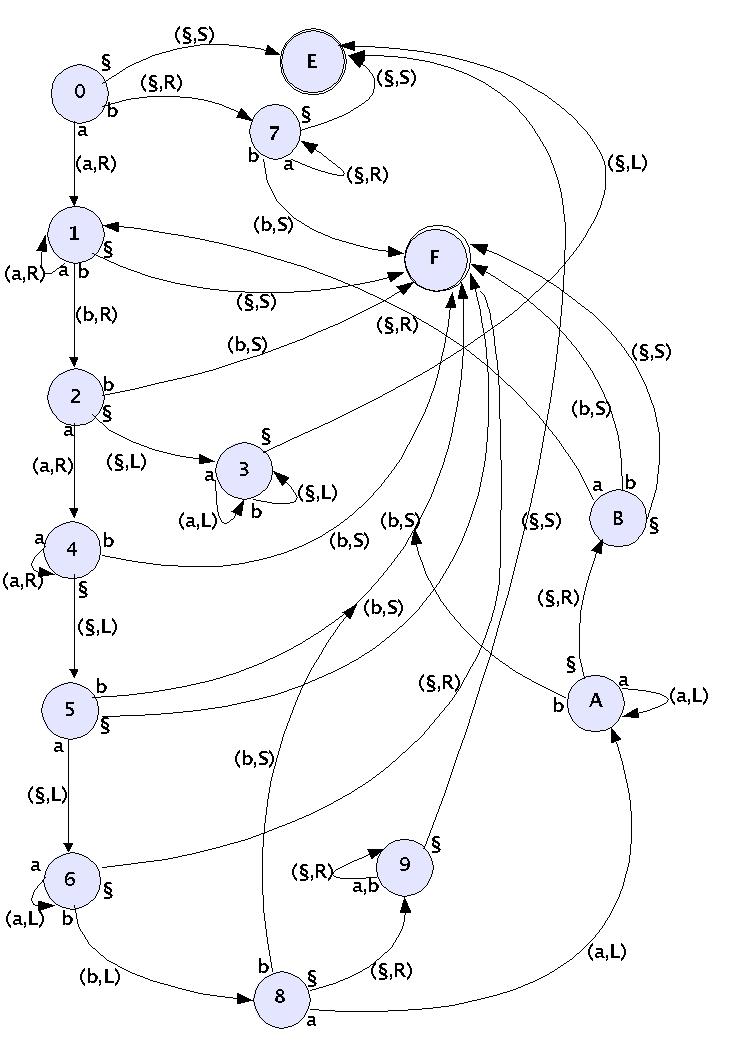
Zustandsgraph zu einer TM
Die Abarbeitung dieses TM-Programms beginnt im Zustand q=0. Der Zustand 0 hat drei Optionen: Liegt nur ein leeres Zeichen a = '§' vor, dann wird auch nur ein leeres Zeichen gedruckt und als Bewegung gilt stop 'S'. Der Folgezustand ist der Zustand q='E'. Liegt das Zeichen a='b' vor, dann wird dieses durch Übershreiben mit '§' gelöscht und eine Bewegung nach rechts m='R' ausgeführt. Der Folgezustand ist in diesem Fall der Zustand q' = '7'. Schliesslich, liegt das Zeichen q='a' vor, dann dann bleibt das Zeichen erhalten, indem das zeichen b='a' gedruckt wird. Als Bewegung wird auch eine Rechtsbewegung m = 'R' ausgeführt. Der Folgezustand ist in diesem Fall der Zustand q' = '1'.
Als Programm geschrieben würde dies lauten:
| q | a | b | m | q' |
|---|---|---|---|---|
| 0 | '§' | '§' | 'S' | E |
| 0 | 'b' | '§' | 'R' | 7 |
| 0 | 'a' | 'a' | 'R' | 1 |
Entsprechend für die anderen Zustände.
| q | a | b | m | q' |
|---|---|---|---|---|
| 0 | '§' | '§' | 'S' | E |
| 0 | 'b' | '§' | 'R' | 7 |
| 0 | 'a' | 'a' | 'R' | 1 |
| 1 | '§' | '§' | 'S' | F |
| 1 | 'b' | 'b' | 'R' | 2 |
| 1 | 'a' | 'a' | 'R' | 1 |
| usw. | . | . | . | . |
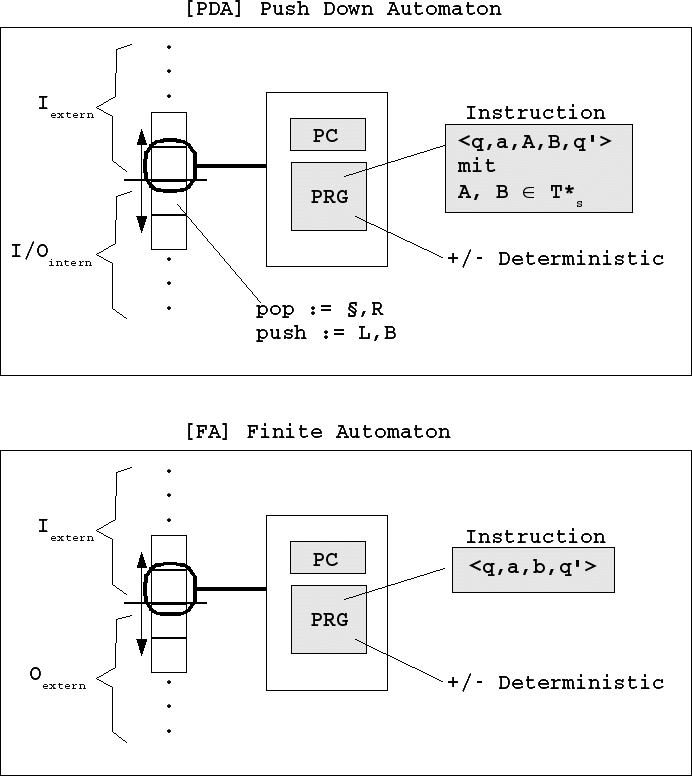
Ein Automat, der weniger mächtig ist als eine TM ist der PDA. Er kann maximal kontextfreie Sprachen (context free languages) erkennen. Betrachtet man den PDA im Vergleich zur TM sieht man sofort, worin der wesentliche Unterschied eines PDA im Vergleich zur TM besteht: während eine TM auf ihrem Band sowohl externen Input und Output lesen und schreiben kann genauso wie auch beliebig internen Input-Output, ist der PDA hier wesentlich beschränkter. Sein Band muss man in zwei Teile aufteilen. Der eine Teile kann nur externen Input lesen, und zwar nur in einer Richtung, und der andere Teil kann benutzt werden, um internen Input-Output zu Lesen und zu Schreiben, allerdings nicht in einer beliebigen Ordnung, sondern in der Weise eines Stapels (stack, Keller): neue Stapelinhalte dürfen nur auf die schon vorhandenen Inhalte draufgelegt werden (die berühmte push-Aktion); gelesen und zuleich gelöscht werden darf nur von oben nach unten (die berühmte pop-Aktion). Allerdings beschränkt sich der Inhalt einer push- oder pop-Aktion dabei nicht nur auf eine einzige Zelle, sondern es können mehrere Zellen gleichzeitig als ein 'Wort' aufgefasst werden. Das erste Wort auf dem Stapel wird meistens als '#' vereinbart. Daran kann der PDA dann erkennen, dass er am 'Boden' des Stapels angekommen ist.
Auch im Falle eines PDA gibt es die deterministische und die nicht-deterministische Variante. Im gegensatz zur TM ist die nicht-deterministische Variante des PDA mächtiger als die deterministische; nur der NPDA kann alle kontextfreie Sprachen erkennen.
Einen Befehl für einen NPDA kann man wie folgt hinschreiben:
<q,a,A,B, q'>
Dabei bedeutet im einzelnen:
q:= der aktuelle Befehl/Zustand
a:= das aktuell gelesene Zeichen
A:= das aktuell gelesene Stapelwort; wenn A = '#', dann Boden des Stapels
B:= das aktuell zu schreibende Stapel-Wort
q':= der nächste auszuführende Befehl
Dabei gilt im Falle von nichtdeterministischen PDAs, dass es zu einer Konfiguration <q,a,A> eben nicht nur eine einzige Fortsetzung geben kann, sondern mehrere.
Auch im Falle eines (N)PDA kann man zum Hilfsmittel des Zustandsgraphen greifen, um das Programm eines (N)PDA zu repräsentieren. Betrachten wir das folgende Beispiel:
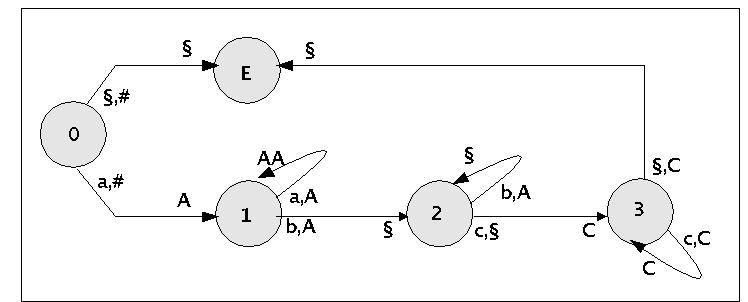
Zustandsgraph zum NPDA für die Sprache anbncm
Die Interpretation dieses Graphen lautet wie folgt: der NPDA beginnt im Zustand q = 0. Im Falle dass das aktuelle Inputzeichen a = '§' leer ist und das aktuelle Stapelzeichen A = '#' den Boden des Stapels anzeigt, dann wird der Stapel unverändert gelassen und in den Folgebefehl q' = E übergegangen. Wenn im Zustand q = 0 allerdings das Inputzeichen a = 'a' gelesen wird und das aktuelle Stapelwort A = '#' ist, dann wird auf den Stapel das neue Stapelwort B = 'A' geschrieben. Der Folgezustand ist dann q' = 1.
| q | a | A | B | q' |
|---|---|---|---|---|
| 0 | '§' | '#' | '§' | E |
| 0 | 'a' | '#' | 'A' | 1 |
Analog die folgenden Befehle:
| q | a | A | B | q' |
|---|---|---|---|---|
| 0 | '§' | '#' | '§' | E |
| 0 | 'a' | '#' | 'A' | 1 |
| 1 | 'a' | 'A' | 'AA' | 1 |
| 1 | 'b' | 'A;' | '§' | 2 |
| usw. | . | . | . | . |
PDA und FA
Der Finite Automat [FA] (oder auch endliche Automat) ist gegenüber dem PDA zusätzlich beschränkt. Sein Band ist auch zweigeteilt, aber er hat keine Möglichkeit, auf dem Band internen Input-Output zwischenzuspeichern. D.h. der FA hat keinen dynamischen Speicher. Sein "Gedächtnis" ist starr, fixiert. Er kann externen Input nur einmal und nur in einer Richtung lesen. Externen Output kann er ebenfalls --falls erwünscht-- nur einmal schreiben und auch das nur in einer Richtung. Seine Befehle sind daher nochmals einfacher als beim PDA:
<q,a,b, q'>
Dabei bedeutet im einzelnen:
q:= der aktuelle Befehl/Zustand
a:= das aktuell gelesene Zeichen
b:= das aktuell zu schreibende Zeichen
q':= der nächste auszuführende Befehl
Wie im Falle der beiden anderen Automaten gibt es auch hier die deterministische und die nicht-deterministische Variante. Später wird gezeigt werden, dass ein DFA nicht schwächer ist als ein NFA! Der NFA lässt sich dadurch realisieren, dass mehr als ein nachfolgebefehl möglich sind.
Ein Zustandsgraph für einen endlichen Automaten zeigt das folgende Bild:
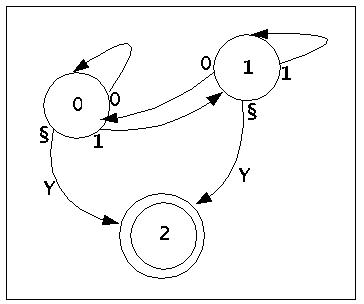
Beispiel eines endlichen Automaten
Die zugehörige Interpretation dieses Zustandsgraphen lautet wie folgt:
Der Automat startet im Zustand q = 0; erkennt er nur ein Blank a = '§', dann schreibt b = 'Y' und er geht in den Folgebefehl q' = 2. Liest er dagegen a = '0', dann schreibt er ein Blank b = '§' (fehlt im Bild) und bleibt im Zustand q' = 0. Liest er dagegen a = '1', dann schreibt er wieder ein Blank b = '§' und geht in den Folgebefehl q' = 1
| q | a | b | q' |
|---|---|---|---|
| 0 | '§' | 'Y' | 2 |
| 0 | '0' | '§' | 0 |
| 0 | '1' | '§' | 1 | usw. | . | . | . |
Rekonstruieren Sie die obigen Beispiele mit den Automaten TM, NPDA und FA in form vollständiger Programme
Beschreiben Sie informell, welche Aufgaben diese Programme lösen.
Weiteres folgt ...