|
|
I-THINF WS 0203 - Vorlesung mit Übung
|
Es werden in dieser Vorlesungen die wichtigen Begriffe im Kontext der Themen Abzählbarkeit, Aufzählbarkeit und Entscheidbarkeit von Sprachen (bzw. Mengen) vervollständigt. Ein Beweis für einen zentralen Satz, dem Halteproblem, wird gegeben. Nach diesen eher grundsätzlichen Betrachtungen wird die konkrete Begrifflichkeit im Umfeld formaler Sprachen weiter entwickelt, so dass der Begriff der formalen Grammatik eingeführt werden kann. Hieran werden sich dann Untersuchungen zu speziellen formalen Grammatiken anschliessen.
Der Begriff der 'Aufzählbarkeit' einer Menge lässt sich über den Begriff der charakteristischen Funktion weiter
differenzieren: Charakteristische Funktion X zur Menge M Rekursive (entscheidbare) Mengen: Sei XM die charakteristische Funktion zur Menge M; wenn
XM turingberechenbar ist, dann ist die Menge M rekursiv (bzw. entscheidbar). Partielle Charakteristische Funktion X* zur Menge M (Rekursive) aufzählbare Mengen: Sei X*M die partielle charakteristische Funktion zur Menge M; wenn
X*M turingberechenbar ist, dann ist die Menge M (rekursiv) aufzählbar. Da Sprachen definiert sind als Teilmengen von Mengen über endlichen Basismengen (= Alphabeten), kann man in obigen
Definitionen entsprechend den Begriff 'Menge' durch 'Sprache' ersetzen, sofern man endliche Basismengen annimmt. 2. Entscheidbarkeit von Sprachen: Definitionen
X:M ---> {0,1} mit
XM(a) = 1, wenn a in M
XM(a) = 0, wenn ¬(a in M)
X*:M ---> {0,1} u {} = mit
X*M(a) = 1, wenn a in M
X*M(a) = undefined, wenn ¬(a in M)
Unter Verwendung der bisher eingeführten Begrifflichkeit kann man jetzt einige interessante Eigenschaften von unterschiedlichen Mengen beweisen.
Aus Sicht der Informatik sind speziell jene Sprachen (= Mengen!) interessant, die Computerprogramme und ihre möglichen Eingaben beschreiben. Wir definieren eine solche Sprache:
LTM = { <m,w > | DTM(m) & w ist eine Eingabe für m}
Satz: Die Sprache LTM ist abzählbar unendlich.
Da nach Voraussetzung sowohl die Programme von universellen Turingmaschinen wie auch die möglichen Eingaben endlich sein müssen, ist jeder einzelne Ausdruck <m',w' > in jedem Fall endlich, d.h. man kann diese Ausdrücke der Länge nach ordnen und innerhalb der Länge nach einer verabredeten Regel sortieren. Wie im Fall der natürlichen Zahlen kann man zu jedem Ausdruck <m',w' > ferner einen eindeutig bestimmten Nachfolger konstruieren.
Es fragt sich jetzt, ob die Sprache LTM auch rekursiv aufzählbar ist, d.h. gibt es eine partielle turingberechenbare charakteristische Funktion XLTM, die zwar alle Elemente von LTM erkennen kann, nicht aber unbedingt die Elemente des Komplementes zu LTM?
Satz: Die Sprache LTM ist rekursiv aufzählbar.
Um sagen zu können, dass die Sprache LTM rekursiv aufzählbar ist, muss es eine Turingmaschine T geben, die alle Elemente von LTM aufzählen kann. Falls dies möglich wäre, könnte die Turingmaschine T bei jeder Eingabe eines Elementes x, in der Liste der aufzählbaren Elemente nachschauen und würde, falls das Element x zu LTM gehört, nach endlich vielen Schritten das Element identifizieren können. Würde das Element x nicht zu LTM gehören, dann wäre die Suche erfolglos; die Turingmaschine T könnte zu keinem Zeitpunkt entscheiden, ob x 'irgendwann vielleicht doch' in der Liste auftaucht. Nun ist klar, dass es eine solche Turingmaschine T gibt, die die Elemente der Sprache LTM aufzählen kann. Sie konstruiert eine Liste aller endlichen Elemente entsprechend der Länge und innerhalb der gleichen Länge nach einer endeutigen Ordnung. Wie lange auch immer diese Liste sein wird, jedes Element in dieser Liste lässt sich nach endlich vielen Schritten identifizieren.
Nun kommt die eigentliche Preisfrage: ist die Sprache LTM vielleicht sogar rekursiv bzw. entscheidbar? Dann könnte man nämlich Computerprogramme P schreiben, die über jedes vorgelegte andere Computerprogramm P' nach endlich vielen Schritten entscheiden könnten, ob dieses Programm P' bei einer beliebigen Eingabe w' nach endlich vielen Schritten anhält. Für die Prüfung der Korrektheit von Computerprogrammen bzgl. bestimmter Aufgaben wäre dies von unschätzbarem Wert. Was man also gerne hätte, wäre der folgende Satz:
(A:m,w)( <m,w > in LTM ==> (E:y)( Turingberechenbare_Charakteristische_Funktion(y,LTM) & y(<m,w > ) = 1, wenn HALT(m,w) & y(<m,w > ) = 0, wenn ¬HALT(m,w)))
Für alle Elemente <m,w > aus der Sprache LTM soll also gelten, dass es eine turingberechenbare charakteristische Funktion y für die Sprache (=Menge) LTM gibt, so dass diese gerade 1 = YES ist, wenn m bei w anhält, und 0 = NO, wenn m bei w nicht anhält. Würde dieser Satz gelten, dann würde man sagen können, dass die Sprache LTM rekursiv (bzw. entscheidbar) ist.
Versuchen wir genau das Gegenteil zu beweisen; wenn dies misslingt, gilt der obige Satz; gilt das Gegenteil, dann ist der Traum ausgeträumt. Das Gegenteil hat logisch die folgende Form:
¬(A:m,w)( <m,w > in LTM ==> (E:y)( Turingberechenbare_Charakteristische_Funktion(y,LTM) & y(<m,w > ) = 1, wenn HALT(m,w) & y(<m,w > ) = 0, wenn ¬HALT(m,w)))
Dies bedeutet:
(E:m,w)¬( <m,w > in LTM ==> (E:y)( Turingberechenbare_Charakteristische_Funktion(y,LTM) & y(<m,w > ) = 1, wenn HALT(m,w) & y(<m,w > ) = 0, wenn ¬HALT(m,w)))
Wegen ¬(A ==> B) gdw ¬(¬A + B) gdw (¬¬A & ¬B) gdw (A & ¬B) bekommen wir:
(E:m,w) ( <m,w > in LTM & ¬(E:y)( Turingberechenbare_Charakteristische_Funktion(y,LTM) & y(<m,w > ) = 1, wenn HALT(m,w) & y(<m,w > ) = 0, wenn ¬HALT(m,w)))
Setzen wir also:
<m',w' > in LTM & ¬(E:y)( Turingberechenbare_Charakteristische_Funktion(y,LTM) & y(<m',w' > ) = 1, wenn HALT(m',w') & y(<m',w' > ) = 0, wenn ¬HALT(m',w'))
Nehmen wir also an, wir haben ein Element <m',w' > in LTM. Dann müssten wir noch beweisen, dass gilt ¬(E:y)(..). Dies ist logisch äquivalent zu (A:y) ¬(...). Und wegen ¬(A & B) gdw (¬A + ¬B) sowie (¬A + C) gdw (A ==> C) können wir den ganzen Ausdruck logisch äquivalent umschreiben zu:
(A:y)( Turingberechenbare_Charakteristische_Funktion(y,LTM) ==> ¬(y(<m',w' > ) = 1, wenn HALT(m',w')) + ¬(y(<m',w' > ) = 0, wenn ¬HALT(m',w')) )
Durch wiederholte Anwendung der logischen Äquivalenzen ¬(A ==> B) gdw ¬(¬A + B) gdw (¬¬A & ¬B) gdw (A & ¬B) auf die beiden ODER-Glieder bekommen wir dann:
(A:y)( Turingberechenbare_Charakteristische_Funktion(y,LTM) ==> [HALT(m',w') & ¬(y(<m',w' > ) = 1)] + [¬HALT(m',w') & ¬(y(<m',w' > ) = 0)] )
Da die Aussage ja für alle y gilt, gilt sie für jedes konkrete y; nehmen wir also an dies wäre ein y*. Könnten wir jetzt unter annahme von y* eines der beiden ODER-Glieder beweisen, dann hätten wir damit den gesamten Satz bewiesen. Die spannende Frage: können wir eines der ODER-Glieder beweisen?
Ein möglicher Beweisansatz besteht darin, die Turingberechenbare_Charakteristische_Funktion y* durch eine universelle Turingmaschine U in dem Sinne zu realisieren, dass auf dem Band von U das Element <m',w' > steht und man zeigen kann, dass y* = U nicht 1 = YES sagt, wenn m' bei w' hält oder umgekehrt, zu zeigen, dass y* = U nicht sagt 0 = NO, wenn m' bei w' nicht anhält.
Was man an dieser Stelle also braucht, das ist eine witzige Idee, wie man solch eine universelle Turingmaschine U = y* baut, die genau das Geforderte liefert. Eine sehr originelle Idee für solch eine universelle Turingmaschine habe ich im Buch von Marvin Minsky gefunden [MINSKY 1967]. Diese möchte ich an dieser Stelle einsetzen (siehe Bild).
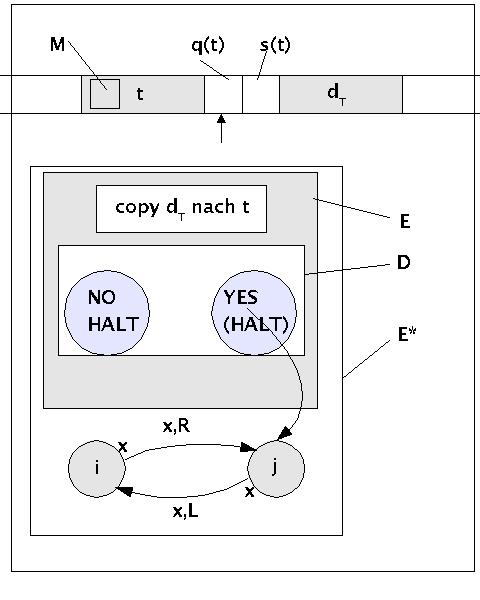
Halteproblem (Idee nach M.Minsky)
Die Ausgangslage ist eine erste universelle Turingmaschine D, die das Paar <m',w' > simuliert und zwei Endzustände (=HALT) besitzt: 1 = YES, wenn m' bei w' stoppt und 0 = NO, wenn m' bei w' nicht stoppt.
Die universelle Turingmaschine D wird dann bei MINSKY zur universellen Turingmaschine E dadurch umgebaut, dass man zu Beginn des Programms von D eine Copy-Funktion einbaut, die die Beschreibung dT der zu simulierenen Turingmaschine m' in die Eingabe t = w' kopiert. Ansonsten verhält sich E wie D.
Schliesslich baut MINSKY die Maschine E nochmals um zur Maschine E*, indem er an den bisherigen Endzustand 1 = YES von D bzw. E zwei neue Zustände i und j so anfügt, dass bei D=E= YES der Zustand j aktiviert wird, dieser führt bei jedem möglichen Ereignis x zum Zustand i und umgekehrt. Bei jedem dieser Übergänge bewegt sich der Schreib-Lesekopf jeweils einmal nach rechts bzw. jeweils einmal nach links. M.a.W. die universelle Turingmaschine y* = U = E* hält bei YES nicht mehr an.
Als letztes nimmt er an, dass in einem speziellen Fall die Beschreibung dT der zu simulierenden Turingmaschine m' = E* ist.
Was bedeutet dies für unseren Beweis. Betrachten wir einfach das Verhalten der universellen Turingmaschine y* = U = E*:
Fall 1: dT = E* hält bei w' (nach MINSKY ist w' auch = E*)
In diesem Fall gilt nach Annahme, dass D=E= YES. Für E* gilt dann aber, dass E* in eine Endlosschleife gerät, und E* nicht
anhält. Dies entspricht genau dem einen ODER-Glied, das zu beweisen ist: [HALT(m',w') & ¬(y*(<m',w' > ) =
1)]
Fall 2: dT = E* hält bei w' nicht
In diesem Fall gilt nach Annahme, dass D=E=E*= NO. Dies entspricht genau dem anderen ODER-Glied, das zu beweisen ist:
[¬HALT(m',w') & ¬(y*(<m',w' > ) = 0)]
Damit wären die entscheidenden Sätze so bewiesen, dass die Widerlegung der allgemeinen Annahme bewiesen ist. Man kann also sagen:
Satz: ¬(A:m,w)( <m,w > in LTM ==> (E:y)( Turingberechenbare_Charakteristische_Funktion(y,LTM) & y(<m,w > ) = 1, wenn HALT(m,w) & y(<m,w > ) = 0, wenn ¬HALT(m,w)))
oder einfacher:
Satz: Die Sprache LTM ist nicht rekursiv (bzw. ist nicht entscheidbar).
Anmerkung: Die Annahme von MINSKY, dass man die Maschine E benötigt, die die Beschreibung der zu simulierenden Turingmaschine dT = m' nach t = w' kopiert, erscheint vom Beweisgang her überflüssig. Verschärfend kommt noch hinzu, dass es sich bei dem Paar <m',w' > um Parameter handelt, die aus einer Partikularquantorersetzung stammen; diese dürfen rein logisch nicht gleich sein! Zu fordern, dass m' = w' steht also auch im Widerspruch zum formalen logischen Rahmen. Wie gesagt, man kann die Forderung der Kopierfunktion und damit die Forderung von E auch fallen lassen, ohne den Beweis zu gefährden und der 'formale Frieden' ist wieder hergestellt.
Auf der Basis des Satzes zum Halte-Problem kann man zahlreiche weitere Sätze beweisen. Für weitere Sätze (Und Beweise) sei auf die Literatur verwiesen.
Nach diesen Beweisen kann man eine erste Hierarchie im Bereich der bisherigen Mengen bzw. Sprachen aufstellen (siehe Bild):
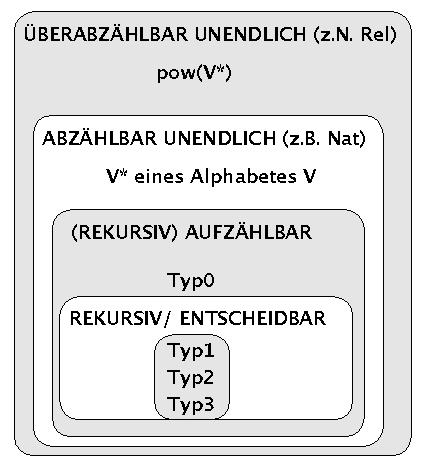
Hierarchie der Berechenbarkeit von Mengen
Die Bezeichnungen Typ0 .. Typ3 beziehen sich auf eine Klassifikation von Sprachklassen nach der Chomsky-Hierarchie. Diese wird in der kommenden Vorlesung erläutert werden.
TURING-BRAIN-Hypothese: In Anlehnung an die vorausgehenden Vorlesungen nennen wir die Hypothese, dass sich das Lernverhalten eines menschlichen Gehirns auf eine universelle Turingmaschine abbilden lässt, die Turing-Brain Hypothese)
Satz: wenn die TURING-BRAIN-Hypothese zurtrifft, dann gilt das Halte-Problem auch analog für Gehirne: für ein Gehirn G ist es prinzipiell nicht möglich, in allen Fällen zu erkennen, wie ein Gehirn G' auf einen Stimulus S reagieren wird.
Der Begriff der formalen Grammtik wird zunächst anhand eines Beispiels aus dem Alltag angeführt.
Wir betrachten einige einfache Sätze der deutschen Sprache.
Hans ist gross.
Hans lacht.
Das Auto fährt schnell.
Susi und Hans treffen sich.
Hans vergisst das rote Buch.
Die Menge der Buchstaben, die in diesem Textfragment vorkommen, sind eine Teilmenge der Zeichen {a,...,z, A, .. Z,ä,ö,ü, Ä,Ö,Ü,.}. Der Einfachheit halber nehmen wir an, dass unser Alphabet V aus allen diesen Zeichen besteht: V = {a,...,z, A, .. Z,ä,ö,ü, Ä,Ö,Ü,.} (man beachte, dass wir den Punkt '.' als Zeichen zulassen!).
Nun betrachten wir die Menge aller Wörter V', die in diesem Textfragmet vorkommen. V' ist nur eine Teilmenge der möglichen Wörter V* über dem Alphabet V:
Hans
ist
gross
lacht
.
Das
Auto
fährt
schnell
Susi
und
treffen
sich
vergisst
rote
Buch
Diese Worte bilden in der Sprache konkrete Objekte, mittels denen kommuniziert wird. Regeln, die über diesen Objekten operieren (bzw. eine Grammatik als Menge von solchen Regeln (s.u.)), müssen über diese konkreten Objekte in einer abstrakteren Weise sprechen. Die Sprachwissenschaftler haben daher schon vor mehr als tausend Jahren sogenannte Wortkategorien erfunden, um Mengen konkreter Wörter unter bestimmten Sammelbezeichnungen (Kategorien, Klassen) zusammenzufassen. Bis heute haftet solchen Wortklassifizierung eine gewisse Beliebigkeit und Unschärfe an. Im Folgenden werden einige Wortkategorien rein experimentell eingeführt. Die Liste von Paaren [Wortkategorie ---> Wort] nennt man im Rahmen einer formalen Grammatik auch ein Lexikon
N ---> Hans, Susi
AUX ---> ist
ADJ ---> gross, schnell, rote
V ---> lacht, fährt, treffen, vergisst
ENDM ---> .
DET ---> Das
CN ---> Auto, Buch
CONJ ---> und
RPR ---> sich
Die Schreibweise 'A ---> b' wird auch Ersetzungsregel (oder Produktion) genannt. Sie besagt, dass die Zeichenkette A duch die zeichenkette b ersetzt werden kann.
Mit diesen Vereinbarungen könnte man das Textfragment jetzt wie folgt umschreiben:
(N,Hans) (AUX,ist) (ADJ,gross) (ENDM,.)
(N,Hans) (V, lacht) (ENDM,.)
(DET,Das) (CN,Auto) (V,fährt) (ADJ,schnell) (ENDM,.)
(N,Susi) (CONJ,und) (N,Hans) (V,treffen) (RPR,sich) (ENDM,.)
(N,Hans) (V,vergisst) (DET,das) (ADJ,rote) (CN,Buch) (ENDM,.)
Da alle diese Wortfolgen Sätze sein sollen (Kategorie 'S'), kann man die Gleichungen einführen:
S ---> N AUX ADJ ENDM
S ---> N V ENDM
S ---> DET CN V ADJ ENDM
S ---> N CONJ N V RPR ENDM
S ---> N V DET ADJ CN ENDM
Die Ersetzungsregeln für S wirken noch sehr umständlich. Man kann versuchen, Optimierungen dadurch einzuführen, dass man 'Zwischenkategorien' einführt, etwa wie folgt:
S ---> NP VP
NP ---> N | DET CN | DET ADJ CN | N CONJ N
VP ---> AUX ADJ | V | V RPR
Damit würde sich dann die folgende Regelmenge ergeben:
S ---> NP VP
NP ---> N | DET CN | DET ADJ CN | N CONJ N
VP ---> AUX ADJ | V | V RPR
N ---> Hans, Susi
AUX ---> ist
ADJ ---> gross, schnell, rote
V ---> lacht, fährt, treffen, vergisst
ENDM ---> .
DET ---> Das
CN ---> Auto, Buch
CONJ ---> und
RPR ---> sich
Mit diesen Regeln könnte man dann einen sogenannten Syntaxbaum erzeugen:
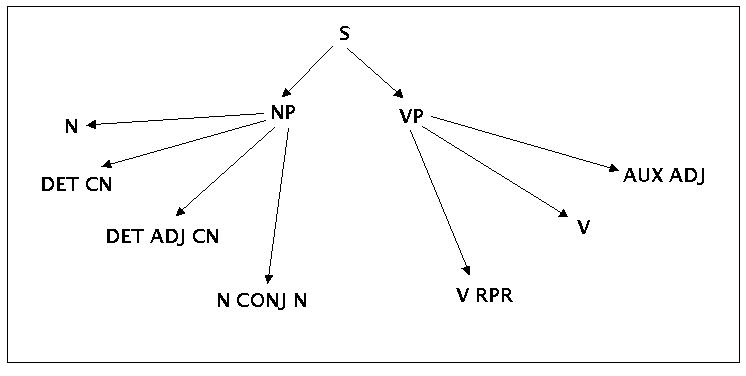
Ein Syntaxbaum zu den Beispielregeln
In Verbindung mit dem Lexikon kann man jetzt alle Sätze generieren, die diese Regeln festlegen. Man stellt leicht fest, dass man jetzt mehr Sätze erzeugen kann, als im ursprünglichen Textfragment vorkommen (=> die Grammtik verallgemeinert, generalisiert!). Ausserdem stellt man fest, dass man Sätze bilden kann, die ein deutscher Sprecher nicht unbedingt als 'volständig korrekt' akzeptieren würde. Beispiele:
Hans vergisst sich (Kann man akzeptieren)
Hans lacht sich (würde man noch ergänzen)
Hans treffen sich (statt treffen erwartet man trifft und noch eine Ergänzung)
Hans fährt sich (mit Ergänzung vielleicht akzeptabel)
Hans und Susi ist gross (mit sind statt ist akzeptabel)
Hans und Susi ist schnell (mit sind akzeptabel)
Hans und Susi ist rote (mit sind rot akzeptabel)
Man sieht, dass man bei natürlichen Sprachen neben der reinen Forma zusätzlich sogenannte implizite Faktoren wie Anzahl der Personen, Geschlecht, Aktionszeit usf. mit berücksichtigen muss. Und diese zusätzlichen impliziten Faktoren interagieren über Wortgrenzen hinweg zwischen verschiedenen Kategorien. Diese und weitere Faktoren stellen hohe Anforderungen an eine formale Grammatik der natürlichen Sprachen. Die Tatsache, dass es bis heute keine wirklich umfassende und allgemein akzeptierte formale Grammatik natürlicher Sprachen gibt, lässt erahnen, dass diese Aufgabe nicht leicht zu lösen ist. Im Rahmen der Informatik beschränkt man sich daher in der Regel auf solche Sprachen, die sich im Rahmen von formalen Grammatiken vollständig beschreiben und damit technisch nutzen lassen (Anmerkung: wie schon in vorausgehenden Vorlesungen bemerkt, ist diese Haltung der Informatik in der Zukunft kaum haltbar; es besteht schon heute die klare Herausforderung an die Informatik, leistungsfähigere sprachliche Schnittstellen bereit zu stellen. Diese können aber nur mit leistungsfähigeren theoretischen Modellen realisiert werden. Dazu gehören notwendigerweise semantische, pragmatische und adaptive Elemente!).
Für formale Grammatiken hat sich eine allgemeine Schreibweise eingebürgert, die wir hier als Struktur im Sinne der Algebra und der Wissenschaftstheorie wiedergeben.
x ist eine formale Grammatik [FG(x)] gdw x = < <V,T,{S} > P> mit
V := Menge der Variablen (oder nicht-terminalen Elemente)
T := Menge der terminalen Elemente
S := Das Startsymbol (steht für Satz ('sentence')); es gilt {S} C V
P := Die Menge der Ersetzungs- bzw. Produktionsregeln. Es gilt allgemein
P C (V u
T)+ x (V u T)*
. Dies bedeutet, auf der linken Seite einer Erzeugungsregel muss mindestens
ein Zeichen stehen, die rechte Seite kann leer sein.
Wenden wir das Schema auf das vorausgehende Beispiel an, dann würden wir folgende konkrete Grammatik bekommen:
x ist die formale Grammatik FG1 gdw x = < <V1,T1,{S} > P1> mit
V1 = {A, .., Z}
T1 = {a,...,z, A, .. Z,ä,ö,ü, Ä,Ö,Ü,.} und es gilt: V1 cut T1 = 0
S = bleibt
P :=
S ---> NP VP
NP ---> N | DET CN | DET ADJ CN | N CONJ N
VP ---> AUX ADJ | V | V RPR
N ---> Hans | Susi
AUX ---> ist
ADJ ---> gross | schnell | rote
V ---> lacht | fährt | treffen | vergisst
ENDM ---> .
DET ---> Das
CN ---> Auto | Buch
CONJ ---> und
RPR ---> sich
Ein Ausdruck wie
CN ---> Auto | Buch
ist eine verkürzende Schreibweise für
CN ---> Auto
or
CN ---> Buch
In den folgenden Vorlesungen werden wir uns mit konkreten Grammatiken und deren Verarbeitung auseinandersetzen.
Machen Sie sich mit dem Beweisgang zum Halteproblem so vertraut, dass Sie einem anderen den Beweis erklären können
.Verfeinern Sie die obige Grammatik FG1 zu FG2, so dass Sie die anzahl der nichtakzeptablen Sätze sich verringert, oder bilden Sie einen neuen Textkorpus und entwickeltn Sie selbst eine neue Grammatik mit den oben dargestellten Zwischenschritten.