1. Einführung

In der vorausgehenden Lehrveranstaltung wurde der Begriff der deterministischen Turingmaschine (DTM) am Beispiel und als formale Definition eingeführt. Es soll heute verdeutlicht werden, inwiefern eine deterministischen Turingmaschine eine Funktion simulieren kann und, wie man eine deterministischen Turingmaschine dazu benutzen kann, jede beliebige deterministische Turingmaschine zu simulieren. Diejenige Turingmaschine, die als solch ein universeller Simulator von deterministischen Turingmaschinen eingesetzt werden kann, die werden wir Universelle Turingmaschine (UTM) nennen. Auf der Basis einer universellen Turingmaschine lassen sich dann eine Reihe interessanter Überlegungen anstellen und Ergebnisse beweisen.

START

2. Funktionsbegriff

Mengentheoretisch ist eine Funktion F eine Relation F C A x B mit der zusätzlichen Eigenschaft der Rechtseindeutigkeit, d.h. für jedes Element a in A gilt, dass es genau ein b in B gibt, das dem Element a zugeordnet ist. F(a) ist von daher eindeutig bestimmt als F(a) = b. Man kann also F auffassen als eine Menge geordneter Paare F = {(a,b), ...}. Die Gesamtheit dieser Paare definiert eine Zuordnungs- bzw. Abbildungsvorschrift. Die Mengen A und B können dabei intern von höherer Komplexität sein, z.B. F C Aⁿ x B^m. Dann würde ein Element p aus F die Form haben p = (<a₁, .., a_n >,<b₁, .., b_m > ). Meistens schreibt man eine Funktion hin in der Form:

F: Aⁿ ---> B^m

und man benutzt eine Funktion in der Form

F(<a₁, .., a_n >) = <b₁, .., b_m > mit <a₁, .., a_n > in Aⁿ und <b₁, .., b_m > in B^m

Definiert man eine neue Funktion, z.B.

f(x,y) = |x-y|

dann führt man im Falle einer Definition durch Gleichheit einen neuen Funktionsnamen 'f' ein (eine Funktionskonstante), mit den beiden Argumenten 'x,y' (das Definiendum), und schreibt rechts vom Gleichheitszeichen einen Ausdruck hin, der als schon definiert gilt (das Definiens), z.B. den absoluten Wert einer Subtraktion von x-y, wenn x,y ganze Zahlen sind. Wichtig ist hier, dass der potentielle Anwender der Funktionsdefinition weiss, wie der definierende Ausdruck '|x-y|' als 'Regel' bzw. als konkrete 'Zuordnungsvorschrift' zu interpretieren ist. Nur dann, wenn der Anwender weiss, wie er vorzugehen hat, um für beliebig vorgegebene x und y zu 'berechnen', wie der endgültige Funktionswert f(x,y) aussieht, nur dann macht diese Schreibweise Sinn.

START

3. Turingberechenbare Funktionen

Im Folgenden betrachten wir solche Funktionen F, bei denen die Zuordnungsvorschrift aus einem Turingmaschinenprogramm besteht, d.h. wenn z.B.

f_t: Nat x Nat ---> Nat

eine Funktion sein soll, deren Werte durch ein Turingmaschinenprogramm t berechnet werden, dann könnte man eine Definition solch einer Funktion in der Form schreiben:

f_t(x,y) = t(x)

Der Ausdruck 't(x)' wäre dann zu lesen als: Der Wert der Turingmaschine t angesetzt auf das Argument x. Man müsste dann nur klar vereinbaren, was es heisst, dass eine Turingmaschine t ausgehend von einem Argument x einen Wert berechnet. Dies wurde in der vorausgehenden Lehrveranstaltung im Rahmen der Definitionen zu einer deterministischen Turingmaschine schon festgelegt, inbesondere wurde auch gesagt, was ein Startzustand und was ein Endzustand ist.

Danach startet eine Turingmaschine mit einem leeren Band, auf dem nur das Argument x steht, im Startzustand q₀ und dem Lese-Schreib-Kopf auf dem ersten Zeichen von x. Dann erzeugt die Turingmaschine eine Ableitung zu x (falls überhaupt möglich) und am Ende der Ableitung steht nur das Ergebnis auf dem ansonsten leeren Band; die Turingmaschine befindet sich in einem Endzustand und der Lese-Schreib-Kopf steht auf dem ersten Zeichen des Ergbnisses

Funktionen, deren Werte auf diese Weise berechnet werden können, sollen turingberechenbare Funktionen heissen.

Die Funktion f(x,y)_substr.tm = subtr.tm(xzy) aus der vorausgehen Lehrveranstaltung ist solch eine turingberechenbare Funktion. Die Argumente 'x,y' sind dabei aus der Menge {a}^* und 'z' ist aus der Menge {b}.

Aus den vorausgehenden Überlegungen ergibt sich aus, dass jedes Turingmaschinenprogramm P, das nach endlich vielen Schritten stoppt, eine Funktion definiert, nämlich P = {(x,y) | x |*--_P y }

START

4. Das Konzept der universellen Turingmaschine

Bisher haben wir nur Turingmaschinen kennengelernt, die eine bestimmte turingberechenbare Funktion berechnen. Interessant wäre es, zu wissen, ob es eine Turingmaschine gibt, die alle möglichen turingberechenbaren Funktionen berechnet. Man könnte es auch so formulieren, ob es eine Turingmaschine geben kann, die alle anderen Turingmaschinen simulieren kann, sozusagen eine universelle Turingmaschine (UTM). Und in der Tat, schon A.M.Turing hat solch einen Beweis in seinem Papier von 1937 mitgeliefert.

Die Grundidee zu diesem Nachweis basiert darauf, dass die universelle Turingmaschine U in der Lage ist, die Beschreibung einer konkreten Turingmaschine T 'zu lesen' und entsprechend den Anweisungen des Programms von T ein Argument x für T berechnet.

Aus heutiger Sicht ist eine universelle Turingmaschine praktisch ein Interpreter-Programm: Man gibt Anweisungen einer bestimmten Sprache L ein und das Interpreter-Programm ist in der Lage, die Ausdrücke der Sprache L zu erkennen und entsprechend vereinbarter Konventionen auszuführen.

Wie könnte solch eine universelle Turingmaschine aussehen? Es gibt -wie immer- mehrere Möglichkeiten, solch eine universelle TM zu beschreiben. Wir folgen hier der sehr schönen Darstellung von M.MINSKY [Computation 1967:Chapt.7]. Nennen wir die Beschreibung einer Turingmaschine t d_t, den aktuellen Zustand q(t), das aktuelle Symbol s(t) und das Band der zu simulierenden Turingmaschine tape_t, dann kann man sich folgende Anordnung vorstellen:

Grundstruktur einer universellen Turingmaschine

Irgendwo auf dem Band steht die Beschreibung der zu simulierenden Turingmaschine d_t. Direkt links davon steht der aktuelle Zustand q(t) von d_t sowie das aktuelle Symbol s(t). Links davon beginnt das Band der zu simulierenden Turingmaschine t. Irgendwo dort -zu Beginn auf dem ersten Zeichen von links der Eingabe für die d_t- gibt es die Marke 'M'; sie signalisiert die aktuelle Position des Lese-Schreib-Kopfes der d_t.

Die Grundidee einer universellen Turingmaschine ist nun die, dass eine UTM eine TM simuliert. Wie in der vorausgehenden Vorlesung vereinbart, simuliert ein Automat U einen Automat T genau dann, wenn für jedes Argument w mit T(w) = w' gilt U(w) = w'. Damit ist vereinbar, dass der Platz- und/oder Zeitbedarf von U grösser oder kleiner ist als von T.

In unserem Fall heisst also eine Simulation der Turingmaschine t durch eine universelle Turingmaschine u, dass das Verhalten von t durch u simuliert wird. Das Verhalten von t ist einerseits bestimmt durch sein Programm P_t sowie von der Inschrift auf dem Band. Startet man im Startzustand q₀ mit einer Anfangskonfiguration, dann ist jede weitere Aktion der Turingmaschine t festgelegt. Für eine Simulation würde es also offensichtlich genügen, das Programm P_t auf das Band von u zu schreiben, dazu einen 'Merkraum' für die jeweils aktuellen Zustände sowie einen Raum für die potentiellen Bandinhalte tape_t von d_t. Die universelle Turingmaschine u benutzt dabei neben der Kodierung von t eine Metakodierung, z.B. schreibt u statt {0,1} in bestimmten Phasen {A,B}.

Ganz allgemein könnte man dann das Verhalten einer UTM u dann wie folgt beschreiben:

Generell wird angenommen, dass die universelle Turingmaschine u zu Beginn ihren Lese-Schreib-Kopf auf dem Feld mit dem aktuellen Zustand q(t) positioniert hat.

1. Identifiziere rechts in der Beschreibung d_t den Abschnitt, dessen Produktion mit 'q(t), s(t)' beginnt.

2. Markiere in dem gefundenen Abschnitt den aktuellen Zustand und das aktuelle Symbol durch eine Metakodierung, nicht aber den Nachfolgezustand q'(t) bzw. das Nachfolgesymbol s'(t).

3. Kopiere dann den Nachfolgezustand und das Nachfolgesymbol (rechts vom aktuellen Zustand) links von d_t in den Bereich des aktuellen Zustands und des aktuellen Symbols

4. Gehe dann nach links bis zu M und ersetze M durch das aktuelle Symbol s(t) und geht ein Feld nach links oder rechts entsprechend dem Wert von m.

5. u druckt die Marke 'M' auf das Feld, merkt sich aber den vorherigen Inhalt und geht nach rechts zum aktuellen Symbol (unmittelbar links vom Programmanfang d_t); dort druckt u das erinnerte Symbol in das Feld (das neue gelesene Symbol).

6. Wiederhole ab Schritt 1.

Nach diesem Schema kann eine universelle Turingmaschine u jedes Programm einer anderen Turingmaschine t abarbeiten.

START

5. Die Beschreibung einer Turingmaschine als Argument für die universelle Turingmaschine

Anhand des Programms P_t einer konkreten Turingmaschine t sei die mögliche Kodierung eines solchen Programms nochmals etwas konkreter illustriert.

Das folgende kleine Programm (im Format des TM-Simulators von A.Jung) beschreibt eine Turingmaschine parity.tm mit zwei Zuständen, die auf dem Band Argumente bestehend aus {0,1}^* daraufhin durchzählt, ob die Anzahl der Einsen ungerade ('odd') ist (= 1) oder gerade ('even') (=0).

0000R
0110R
0 E0S

1010R
1100R
1 E1S

E0E0S
E1E1S
E E S
 

Eine Übersetzung dieser TM in eine Kodierung für eine universelle Turingmaschine könnte folgendermassen vorgenommen werden:

1. Alle Werte werden binär dargestellt

2. Im Beispiel nehmen wir an, dass es nur 2ⁿ mit n=2-viele Zustände gibt

3. L := 0, R := 1

4. Startzustand ist '00' und Endzustand ist '11'

Dies ergibt:

X0000001X0010101X00 1100X0100101X0110001X01 1110X1101100X1111110X11 11 0Y

'X' markiert jeweils den Beginn einer Produktion und 'Y' markiert das Ende des Programms.

Für die gesamte universelle Turingmaschine würde sich dann folgende Kodierung empfehlen:

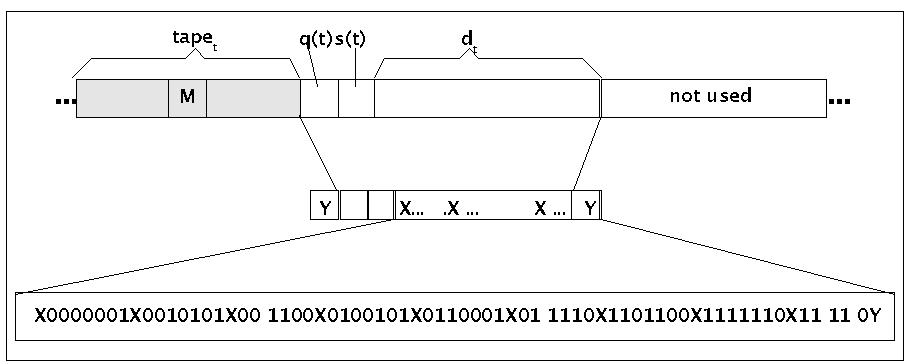
Details der Grundstruktur einer universellen Turingmaschine

Die Metazeichen 'Y' markieren also einmal rechts das Ende der Beschreibung d_t und links den Anfang des zu simulierendes Bandes tape_t der zu simulierenden Turingmaschine t. Zugleich markiert das linke Y auch den beginn des aktuellen Zustandes.

START

6. Ein Beispiel

Siehe Übungsaufgaben

START

7. Warum eine universelle Turingmaschine potentiell auch eine universelle Lernmaschine ist

An dieser Stelle soll eine kurze Reflexion eingeschoben werden ob, und falls ja: in welchem Sinne, eine universelle Turingmaschine lernen kann.

Der Ausgangspunkt für diese Überlegung ist gegeben durch Systeme, die als Teil von Umgebungen ('environments') bestimmte Aufgaben erfüllen sollen (siehe Grafik):

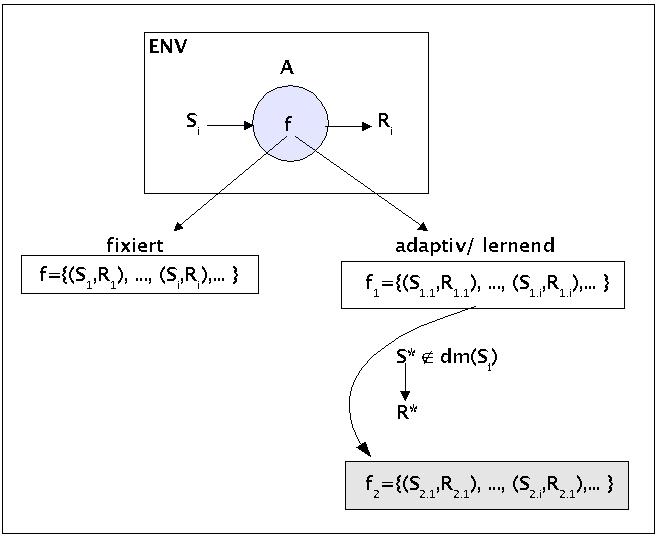
Fixierte und adaptive Systeme

Falls die Aufgabe, die das System bewältigen soll, gut beschrieben vorliegt, existiert eine Auflistung jener Teilsituationen S_i, in denen das System A in einer bestimmten Weise reagieren soll R_i. Die Gesamtheit dieser (S_i, R_i)-Paare konstituiert eine Zuordnungsvorschrift bzw. eine Abbildung bzw. eine Funktion f; idealerweise ist das System A in der Lage, diese Funktion f als Systemfunktion zu realisieren.In fast allen heute bekannten Fällen sind die Systemfunktionen von Maschinen 'fest', 'fixiert'. Maschinen können sich selbst in der Regel nicht ändern.

Von biologischen Systemen wissen wir, dass sie in begrenztem Umfang ihr Verhalten ändern können. Treten Situationen auf, die für ihr Überleben wichtig sind, die bislang noch nicht in ihrem Verhalten vorgesehen waren, dann können sie aufgrund dieser neuen Umstände ihr Verhalten von einer Funktion f1 zu einer Funktion f2 begrenzt ändern.

Von biologischen System wissen wir auch, das deren Verhalten durch ihr Nervensystem gesteuert wird. Ein Nervensystem ist ein Netzwerk einzelner Nervenzellen. Die Neurobiologie weiss heute (siehe z.B. [SHEPHERD 1994], [DUDEL et al. 1996]), dass Nervenzellen die Eigenschaft besitzen, dass sie sich ereignisabhängig sowohl einzeln als auch im koordinierten Verband in bestimmten Umfang und u.U. nur für bestimmte Zeitintervalle 'verändern'/ 'umbauen' können. Diese Veränderungen ziehen Änderungen in ihrer Systemfunktion nach sich. Dies wiederum drückt sich in einem veränderten Verhalten aus. M.a.W. weil sich das Nervensystem biologischer Systeme, welches das Verhalten dieser Systeme steuert, selbständig ändern kann, können biologische Systeme ihr eigenes Verhalten begrenzt ändern, ein Vorgang, der sich für uns als 'Lernen' manifestiert.

Es stellt sich jetzt die grundsätzliche Frage, ob eine universelle Turingmaschine diese Adaptivität biologischer Systeme im Prinzip nachvollziehen kann. Falls diese Frage mit Ja zu beantworten wäre, dann müsste man sagen, dass universelle Turingmaschinen potentiell lernfähig sind.

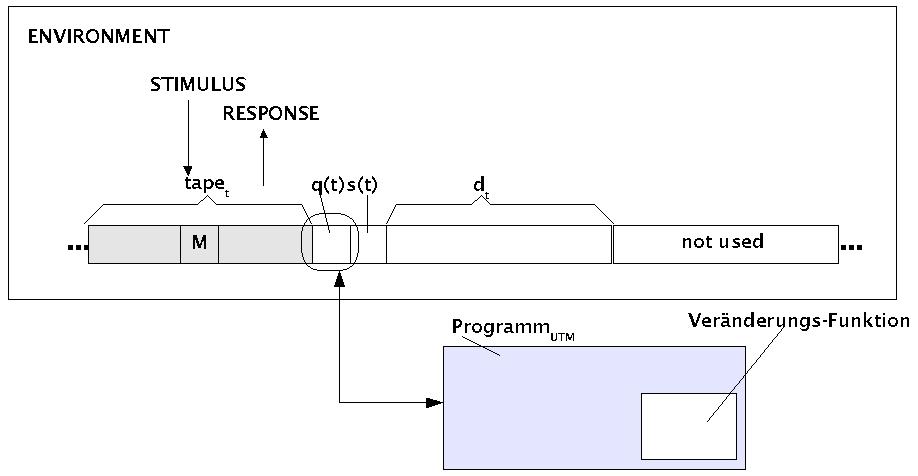
Eine universelle Turingmaschine als potentielle Lernmaschine

Dass eine universelle Turingmaschine potentiell lernfähig ist, das kan man sich relativ leicht klar machen. Wie aus der vorausgehenden Grafik ersichtlich, hängt das Verhalten einer universelle Turingmaschine zunächst von derjenigen Turingmaschine t ab, deren Beschreibung d_t sich gerade auf dem Band befindet. Wir wissen mittlerweile, dass eine Beschreibung einer Turingmaschine mit einer Funktion gleichzusetzen ist. Dies bedeutet, die universelle Turingmaschine u besitzt zunächst eine starre, fixierte Funktion, vorgegebene durch die Beschreibung d_t. Zugleich sieht man aber auch, dass die universelle Turingmaschine u im Prinzip die vorgegebene Beschreibung d_t abändern könnte. Man müsste dazu nur das Programm P_U der universelle Turingmaschine u um ein Programmteil P_U.L erweitern, in dem genau jene Regeln stehen würden, die festlegen, wann die vorgegebene Beschreibung einer zu simulierenden Turingmaschine t wie abzuändern ist. Das Programm P_U einer universellen adaptiven Turingmaschine bestände dann aus zwei Teilen:

P_U = P_U.T + P_U.L

P_U.T wäre jener Teil, der sagt, wie man ein vorgegebenes Programm d_t simuliert und der Programmteil P_U.L, der besagt, wie man ein vorgegebenes Programm d_t unter bestimmten Bedingungen wieder abändert.

Die Analogie zu biologischen Systemen kann man in mindestens zwei Richtungen noch erweitern.

1. Einmal kann man sich noch ein Environment zum System hinzudenken, das so funktioniert, dass die Argumente auf dem Band der Turingmaschine jene Stimuli sind, die von diesem Environment ausgehen. Ferner werden die Reaktionen der Turingmaschine als Response-Ereignis aufgefasst, die in das Environment zurückwirken.

2. Zum anderen kann man sich vorstellen, dass man mittels einer universelle Turingmaschine u das Nervensystem biologischer Systeme 'nachbaut'. Man gibt eine Struktur T_NN vor (das Nervensystem zum Zeitpunkt x als eine Turingmaschine) und legt das Lernmodul P_U.L so an, dass es die Veränderungen an T_NN genauso simuliert, wie sie am 'richtigen' Nervensystem auch geschehen würden.

START

8. Übungsaufgabe

1. Bilden sie ein Team von 5 Mitgliedern

2. Erstellung Sie gemeinsam einen Text mit Namen und Matr.Nr. der AutorenInnen. Abgabe einer Kopie des Textes an den Dozenten vor Beginn der Übung.

3. Präsentation der Lösung als Team vor der gesamten Gruppe. Präsentationszeit (abhängig von der Gesamtzahl der Teams) 3-5 Min.

4. Arbeiten Sie eine der folgenden Turingmaschinen aus, die dann zusammen eine universelle Turingmaschine ergeben sollen:

   1. locator.tm := Ausgehend vom aktuellen Zustand und aktuellem Symbol soll rechts in der Beschreibung d_t der Abschnitt gefunden werden, dessen Produktion mit 'q(t), s(t)' beginnt. Es sollen dann in dem gefundenen Abschnitt der aktuelln Zustand und das aktuelle Symbol durch eine Metakodierung {A für 0, B für 1} markiert werden, nicht aber der Nachfolgezustand q'(t) bzw. das Nachfolgesymbol s'(t) (höchstens 7 Zustände).

   2. copy.tm := Kopiere den Nachfolgezustand und das Nachfolgesymbol (rechts vom aktuellen Zustand) in den Bereich des aktuellen Zustands und des aktuellen Symbols links von d_t (höchstens 7 Zustände).

   3. marker.tm := Gehe nach links bis zu M und ersetze M durch das aktuelle Symbol s(t) und geht ein Feld nach links oder rechts entsprechend dem Wert von m. Drucke die Marke 'M' auf das neue Feld, dabei soll der vorherige Inhalt 'gemerkt' werden. Gehe dann nach rechts zum aktuellen Symbol (unmittelbar links vom Programmanfang d_t); dort drucke das erinnerte Symbol in das Feld (das neue gelesene Symbol) (höchstens 7 Zustände?).

5. Die Gruppen sollten versuchen, sich so abzustimmen, dass zum Schlus alle Teile vorliegen und man sie zu einem Programm zusammenbauen könnte. Stellen Sie ihre Programme als Zustandsgraphen dar. Falls möglich als Grafik im JPEG-Format auf Diskette.

START