Achtung : Skript gibt den mündlichen Vortrag nicht vollständig wieder  !!!
                  

1. Einführung

In dieser und der nächsten Vorlesung soll das Konzept der kontextfreien Grammatik sowie die damit verbundenen Parsingmethoden eingehender vorgestellt werden. Von allen bekannten Grammatiktypen haben die kontextfreie Grammatik mit ihren vielfältigen Varianten die grösste praktische Bedeutung. Einige der Anwendungsszenarien, in denen solche Grammatiken zur Anwendung kommen, sind die folgenden:

• Naürlichsprachliche Schittstellen




• Hilfesysteme




• Befehlsschnittstellen




• Mustererkennung ('Pattern Recognition')




• Bildschirmlayout-Masken




• Textübersetzung




• Sprachübersetzungübersetzung




• Spracherkennung




• Sprachsynthese




• Bildbearbeitung




• usw.

Entsprechend der grossen praktischen Bedeutung ist das Gebiet der kontextfreien Grammatiken sehr umfangreich. Wir werden in der verbleibenden Zeit nur einige wenige Grundkonzepte vorstellen können. Wer sein Wissen gezielt vertiefen will, dem seien neben [SCHÖNING 2001] und [HEDSTÜCK 2002] die beiden theoretisch orientierten Überblicksartikel von [J-M.AUTEBERT/ J.BERSTEL/ L.BOASSON 1997] und [K.SIKKEL/ A.NIJHOLT 1997] empfohlen sowie die eher praxisorientierte Einführung von [Alfred V.AHO/ Ravi SETHI/ Jeffrey D.ULLMAN 1988].

START

2. Kontextfreie Grammatiken; Normalformen; (E)BNF

Für verschiedene theoretische Zwecke (spezielle Beweise) wie auch für bestimmte praktische Aufgaben (z.B. spezielle Parsing-Algorithmen) wurden unterschiedliche Normalformen entwickelt, in die hinein sich eine formale Grammtik vom Typ2 übersetzen lässt. Einige der wichtigsten Normalformen seien hier aufgelistet (siehe dazu ausführlicher [J-M.AUTEBERT/ J.BERSTEL/ L.BOASSON 1997]):

• Kontextfreie Grammatik (Context Free Grammar [CFG]): (u,w) in P dann u in V und w in (V u T)^*




• Schwache Chomsky Normalform [WCNF]: (u,w) in P dann u in V und w in V^* oder w in T u {§}




• Chomsky Normalform [CNF]: wenn Schwache Chomsky Normalform und w in V^* mit |w| < 2




• Greibach Normalform [GNF]: (u,w) in P dann u in V und w in AV^*




• Quadratische Greibach Normalform [2GNF]: wenn Greibach Normalform [GNF] und |V^*| = 2




• Doppelte Greibach Normalform [TGNF]: (u,w) in P dann u in V und w in AV^*A oder A




• Operator Normalform [ONF]: (u,w) in P dann u in V und w in (V u T)^* und w enthält keine zwei aufeinanderfolgenden Variablen (d.h. zwischen zwei Variablen kommt mindestens ein terminales Zeichen vor).

Alle diese Normalformen sind untereinander äquivalent. Ein Beispiel für die Chomsky Normalform [CNF] wird in dieser Vorlesung gegeben; in der nächsten Vorlesung wird ein Beispiel in Greibach Normalform [GNF] verwendet werden.

An dieser Stelle ist auch die sogenannte Backus-Naur Form [BNF] bzw. die Extended Backus-Naur-Form [EBNF] zu erwähnen (siehe für eine ausführlichere Übersicht hier ( mit Link auf eine ausführliche Darstellung von EBNF).

Die BNF und die EBNF-Notation ist ebenfalls äquivalent zu einer kontextfreien Grammatik. Sie eignet sich insbesondere zur Darstellung von kontextfreien Grammatiken in computerlesbarer Form.

3. Von CFG zu CNF und GNF

Es wird jetzt das Beispiel einer konkreten CFG g6 gegeben. Anhand eines allgemeinen Verfahrens wird diese Grammatik g6 dann in eine CNF umgeformt. Die Beispielsprache aⁿbⁿc^m wird auch weiter unten im Zusammenhang mit einem Kellerautomaten verwendet werden.

Zielobjekt ist die Sprache L = {aⁿbⁿc^m | n,m > 1}:

Es sei FG(g6,2) mit V_g6 = {S,A,B} und T_g6 = {a,b,c} und

P_g6 = {
S ---> AB
A ---> ab | aAb
B ---> c | cB
}

Beispiele von Ableitungen mit g6:

1. S




2. AB




3. abB




4. abc

1. S




2. AB




3. aAbB




4. aabbB




5. aabbc

1. S




2. AB




3. aAbB




4. aabbB




5. aabbcB




6. aabbccB




7. aabbccc

Satz: Wenn es eine kontextfreie Grammatik g gibt, dann kann man eine kontextfreie Grammatik g' in CNF effektiv konstruieren.

Für die Konstruktion wird das folgende Verfahren vorgeschlagen (siehe [J-M.AUTEBERT/ J.BERSTEL/L.BOASSON 1997:125]

1. Zu jedem terminalen Zeichen a der Grammatik g wird ein nichtterminales Zeichen X_a der Grammatik g' eingeführt; zugleich wird jedes terminale Zeichen a in g durch das neue Zeichen X_a in g' ersetzt. Dann wird für jedes terminale Zeichen a in g' die Regel X_a ---> a hinzugefügt.




2. Für alle nichtterminalen Worte mit Länge grösser 2 werden diese Worte von links nach rechts so zerlegt, dass jeweils zwei Variablen X₁X₂REST durch eine neue Variable Y ersetzt werden und die Regel V ---> X₁X₂ hinzugefügt wird.

Wendet man dieses Verfahren auf die Grammatik g6 an, dann erhält man folgendes Ergebnis:

1. Anwendung von Regel 1: V_g6' = {S,A,B,C,D,E} und T_g6' = {a,b,c} und
   
   P_g6' = {
   S ---> AB
   A ---> CD | CAD
   B ---> E | EB
   C ---> a
   D ---> b
   E ---> c
   }




2. Anwendung von Regel 2: V_g6' = {S,A,B,C,D,E,F} und T_g6' = {a,b,c} und
   
   P_g6' = {
   S ---> AB
   A ---> CD | FD
   B ---> E | EB
   F ---> CA
   C ---> a
   D ---> b
   E ---> c
   }

Beispiele von Ableitungen:

1. S




2. AB




3. CDB




4. aDB




5. abB




6. abc

1. S




2. AB




3. FDB




4. CADB




5. aADB




6. aCDDB




7. aaDDB




8. aabDB




9. aabbB




10. aabbc

1. S




2. AB




3. FDB




4. CADB




5. CCDDB




6. CCDDEB




7. CCDDEEB




8. aCDDEEB




9. aaDDEEB




10. aabDEEB




11. aabbEEB




12. aabbcEB




13. aabbccB




14. aabbccc




15. aabbccc

Die Umwandlung in eine Greibach Normalform (GNF) benutzt die Umwandlung in eine Chomsky Normalform als ersten Schritt. Die nächsten Umwandlungsschritte sind allerdings etwas aufwendiger (siehe dazu die Darstellung in [SCHÖNING 2001:54ff]).

4. Kellerautomaten [PDA]

Diejenigen Automaten, die in der Lage sind, alle kontextfreien Sprachen zu erkennen, das sind die Kellerautomaten ('push down automata' [PDA]). Ausgehend von einer Turingmaschine kann man das Prinzip von Kellerautomaten wie folgt einführen (siehe Bild):

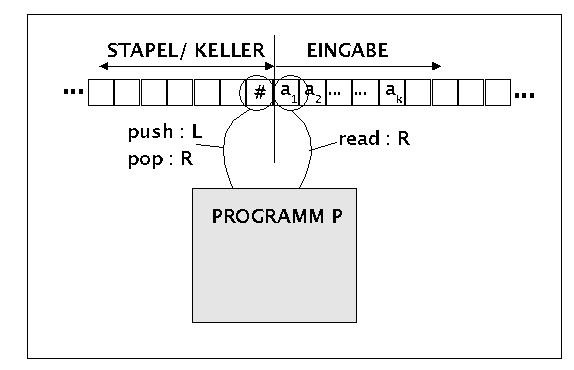
Prinzipschaltbild eines Kellerautomaten

Statt nur einen Schreib-Lese-Kopf besitzt ein Kellerautomat zwei Leseköpfe, wobei der eine auch schreiben kann. Der eine Lesekopf -nennen wir ihn KE- ist dazu da, dass er eine Eingabe E lesen kann. Im Bild wird angenommen, dass dies von links nach rechts geschieht; man könnte die Vereinbarung aber auch umgekehrt treffen. Das Lesen der Eingabe E = a₁,a₂, ..., a_k geschieht einmalig und ist unumkehrbar; mit jedem gelesenen Zeichen wandert der Lesekopf KE ein Feld nach rechts. Der andere Schreib-Lesekopf -nennen wir ihn KS-, beginnt in einer Ausgangsposition und kann mittels Schreiben (Operation 'push') ein Feld nach links bewegt werden, und mittels Lesen (Operation 'pop') ein Feld nach rechts. Der Bereich des Bandes, der von KS gelesen und geschrieben werden kann, funktioniert hier als ein Stapel ('stack'), der für das Programm wie ein Speicher/ Gedächtnis/ Keller fungiert. In der hier angenommenen Version eines Kellerautomaten hat der Stapel zu Beginn das Start-Keller-Zeichen '#' (Doppelkreuz). Vereinbarungsgemäss steht KS zu Beginn auf dem Feld mit dem Zeichen '#' und KE auf dem ersten Feld der Eingabe, von links nach rechts.

Def.: PDA(a) gdw a = << Q, T_i, T_s, {q₀}, {#}>, P >

mit

1. Q: Endliche Menge von Zuständen




2. T_i: Alphabet für mögliche Eingaben




3. T_s: Alphabet für den Stapel/ Keller; T_i cut T_s = 0




4. q₀: der Startzustand; q₀ in Q




5. # : das Startelement für den Stapel; '#' in T_s




6. P: das Programm von a bzw. die Überführungsfunktion:
   
   

Das Programm P eines Kellerautomaten berechnet in Abhängigkeit von einem aktuellen Zustand q aus Q, einem aktuell gelesenen Zeichen a aus T_i (aus der Eingabe) sowie einem aktuell gelesenen Zeichen A aus T_s (dem Stapel/ Keller) die nächste Aktion. Dies kann nicht-deterministisch geschehen oder deterministisch.

Während bei Turingmaschinen die deterministische Turingmaschine den Standardfall darstellt, ist es bei Kellerautomaten die nichtdeterministische Variante. Die deterministische Variante von Kellerautomaten ist schwächer als die nichtdeterministische. Nur der nichtdeterministische Kellerautomat erkennt alle Sprachen, die von einer kontextfreien Grammatik erzeugt werden können.

4.1 Nichtdeterministische Kellerautomaten [NPDAs]

Def.: NPDA(a) gdw PDA(a) und es gilt

P: Q x (T_i u {§}) x (T_s u {§}) ---> 2e^{(Q x T_s*)}

(Anmerkung: '2e' repräsentiert die Menge aller endlichen Teilmengen)

Diese Überführungsfunktion P besagt also, dass in Abhängigkeit von einem aktuellen Zustand q aus Q, einem aktuell gelesenen Zeichen a aus T_i (aus der Eingabe) sowie einem aktuell gelesenen Zeichen A aus T_s (dem Stapel/ Keller) eine endliche Menge von Folgezuständen bestimmt wird, wobei jedem Folgezustand q' ein Wort B₁...B_k über T_s* korrespondiert, d.h. das oberste Element des Stapels A wird durch ein neues Wort B₁...B_k ersetzt. Ist das Wort B₁...B_k = 0 (d.h. 'leer'), dann entspricht dies der 'pop'-Aktion, d.h. das oberste Element des Stapels wird entfernt.

Das Programm eines nichtdeterministische Kellerautomaten besteht damit also aus einer Menge von 4-Tupeln der Art:

< q,a,A,{(q'₁,B₁), (q'₂,B₂)...}> (B_i Wort über T_s*)

Vergleicht man dies mit den Aktionen <q,a,q',b,m > einer deterministischen Turingmaschine, dann fällt sofort auf, dass ein nichtdeterministischer Kellerautomat neben den Eingabezeichen eben noch von dem Zustand des Stapels gesteuert wird. Ferner wird nicht allgemein auf das Band geschrieben, sondern nur auf jenen Bereich, der für den Stapel reserviert ist. Schliesslich sind die Bewegungen m der Turingmaschine nur implizit gegeben: ein leeres Wort entspricht der Aktion 'pop', d.h. gehe ein Feld nach rechts, und ein nicht-leeres Wort bedeutet die Aktion 'push', d.h. gehe ein Feld nach links. Man kann also schon von dieser Architektur her augenfällig erkennen, dass der nichtdeterministische Kellerautomat gegenüber der Turingmaschine dadurch beschränkt ist, dass er für einen reservierten Teil des Bandes nur 'passiv' lesen kann.

Analog zur Turingmaschine und zum endlichen Automaten benötigen wir hier auch wieder den Begriff der durch einen nichtdeterministischen Kellerautomaten erkennbaren Sprache:

Def.: L_NPDA(a) = {x in T_i* | NPDA(a) & (E:q)( <q₀,x,#> |---_a* <q,§,§> & q in Q_a )}

Die durch einen nichtdeterministischen Kellerautomaten a erkennbaren Sprache L_NPDA besteht also aus denjenigen Worten x über T_i*, für die gilt, dass ausgehend von dem Anfangszustand q₀, dem Wort x, und dem Keller-Startsymbol # ein Zustand q so abgeleitet werden kann, dass sowohl die Eingabe wie auch der Keller leer (= §) sind.

Um den dabei zur Verwendung kommenden Ableitungsbegriff '|---_a*' benutzen zu können, muss dieser zuvor eingeführt worden sein. Dies wird hier -analog zum Fall der Turingmaschine- über den Begriff der Konfiguration geleistet.

Zu jedem Zeitpunkt ist der aktuelle Zustand eines Kellerautomaten eindeutig gegeben durch den aktuellen Zustand q, durch den aktuellen Rest der Eingabe a₁...a_n sowie durch den aktuellen Kellerinhalt k₁...k_m, also

< q,a₁...a_n, k₁...k_m> in Q x (T_i* u {§}) x (T_s* u {§}).

Ein solches 3-Tupel soll eine Konfiguration heissen. Durch Anwendung des Programms P() geht diese Konfiguration in eine Folgekonfiguration über mit

< q',a₁...a_n, B₁...B_r...k_m>,
falls P(q,§,k₁)
oder in
< q',a₂...a_n, B₁...B_r...k_m>,
falls P(q,a₁,k₁)

Def.: k ist eine Konfiguration vom NPDA a: CONFIG(k,a) gdw NPDA(a) & k in Q x (T_i* u {§}) x (T_s* u {§})

Def.: k' ist eine direkte Ableitung von k mit NPDA a: DABL(k,k',a) gdw CONFIG(k,a) & CONFIG(k',a) & (E:q,q',a₁,...,a_n,k₁, ...,k_m,B₁,...,B_r)(

(i) [ k=< q,a₁...a_n, k₁...k_m> & k'= < q',a₁...a_n, B₁...B_r...k_m> & <q,§,k₁,{...,(q',B₁...B_r),...} > in P]

or

(ii) [ k=< q,a₁...a_n, k₁...k_m> & k'= < q',a₂...a_n, B₁...B_r...k_m> & <q,a₁,k₁,{...,(q',B₁...B_r),...} > in P]

)

Def.: x ist ableitbar mit NPDA a: ABL(x,a) gdw (E:t,n,q)( t ist ein Tupel der Länge n & q in Q_a & (A:i,j)( i,j in dm(t) & j=i+1 ==> DABL(t_i,t_j) & t₀ = <q₀,x,#, > & t_n-1 = <q,§,§ >))

Wie üblich soll folgende Schreibweise vereinbart werden:

k |--_a k' gdw DABL(k,k',a)

<q₀,x,#, > |--_a* <q,§,§ > gdw ABL(x,a)

Anmerkung: Eine interessante Variante von (N/D)PDAs bilden jene, in denen man mehr als ein spezielles Kellerzeichen einführt, nämlich sogenannte Fehler-Zeichen F*. Dise kann man benutzen, um unerwünschte Anordnungen von Eingabezeichen als 'Fehler' zu markieren. Man könnte dann neben dem Begriff 'ableitbar in a' auch den Begriff 'fehlerhaft in a' definieren.

Analog zu den anderen Automaten kann man auch im Fall des Kellerautomaten einen passenden Zustandsgraphen definieren (siehe nachfolgendes Bild).

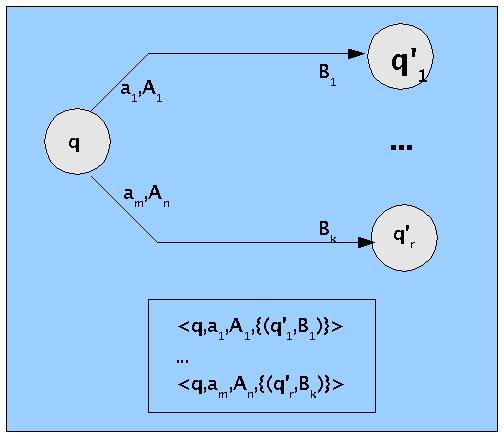
Zustandsgraph zum Kellerautomaten

Auf diese Weise lassen sich einfache Automaten übersichtlich darstellen. Im folgenden geben wir zu der Sprache L = {aⁿbⁿc^m | n,m > 1} einen Kellerautomaten an, der diese Sprache erkennen kann.

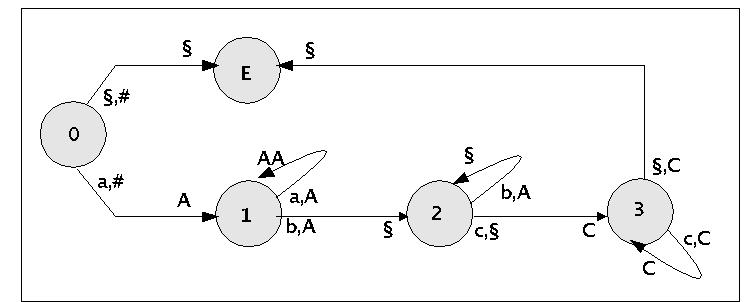
Zustandsgraph zum Kellerautomaten für die Sprache aⁿbⁿc^m

Das zugehörige Programm lautet wie folgt:

1. <0,§,#,{(E,§)} >




2. <0,a,#,{(1,A)} >




3. <1,a,A,{(1,AA)} >




4. <1,b,A,{(2,§)} >




5. <2,b,A,{(2,§)} >




6. <2,c,§,{(3,C)} >




7. <3,c,C,{(3,C)} >




8. <3,§,C,{(E,§)} >




9. <E,§,§,{(E,§)} >

Damit lassen sich folgende Ableitungen durchführen:

1. <0,abc,# >




2. <1,bc,A >




3. <2,c,§ >




4. <3,§,C >




5. <E,§,§ >

1. <0,aabbc,# >




2. <1,abbc,A >




3. <1,bbc,AA >




4. <2,bc,A >




5. <2,c,§ >




6. <3,§,C >




7. <E,§,§ >

4.2 Deterministische PDAs

Def.: DPDA(a) gdw PDA(a) und es gilt

P: Q x (T_i u {§}) x (T_s u {§}) ---> Q x T_s*

Diese Überführungsfunktion P besagt also, dass in Abhängigkeit von einem aktuellen Zustand q aus Q, einem aktuell gelesenen Zeichen a aus T_i (aus der Eingabe) sowie einem aktuell gelesenen Zeichen A aus T_s (dem Stapel/ Keller) genau ein Folgezustand bestimmt wird, wobei jedem Folgezustand q' ein Wort B₁...B_k über T_s* korrespondiert, d.h. das oberste Element des Stapels A wird durch ein neues Wort B₁...B_k ersetzt. Ist das Wort B₁...B_k = 0 (d.h. 'leer'), dann entspricht dies der 'pop'-Aktion, d.h. das oberste Element des Stapels wird entfernt.

Das Programm eines nichtdeterministische Kellerautomaten besteht damit also aus einer Menge von 4-Tupeln der Art:

< q,a,A,(q',B₁...B_k) >

Die Begriffe Konfiguration, direkte Ableitung sowie Ableitbar sind analog zu den Begriffe im Falle des NPDA zu bilden.

Def.: k ist eine Konfiguration vom DPDA a: CONFIG(k,a) gdw DPDA(a) & k in Q x (T_i* u {§}) x (T_s* u {§})

Def.: k' ist eine direkte Ableitung von k mit DPDA a: DABL(k,k',a) gdw CONFIG(k,a) & CONFIG(k',a) & (E:q,q',a₁,...,a_n,k₁, ...,k_m,B₁,...,B_r)(

(i) [ k=< q,a₁...a_n, k₁...k_m> & k'= < q',a₁...a_n, B₁...B_r...k_m> & <q,§,k₁,(q',B₁...B_r) > in P]

or

(ii) [ k=< q,a₁...a_n, k₁...k_m> & k'= < q',a₂...a_n, B₁...B_r...k_m> & <q,a₁,k₁,(q',B₁...B_r) > in P]

)

Def.: x ist ableitbar mit DPDA a: ABL(x,a) gdw (E:t,n,q)( t ist ein Tupel der Länge n & q in Q_a & (A:i,j)( i,j in dm(t) & j=i+1 ==> DABL(t_i,t_j) & t₀ = <q₀,x,#, > & t_n-1 = <q,§,§ >))

Wie üblich soll folgende Schreibweise vereinbart werden:

k |--_a k' gdw DABL(k,k',a)

<q₀,x,#, > |--_a* <q,§,§ > gdw ABL(x,a)

Dann kann man definieren:

Def.: L_DPDA(a) = {x in T_i* | DPDA(a) & (E:q)( <q₀,x,#> |---_a* <q,§,§> & q in Q_a )}

Weitere Ausführungen zu Kellerautomaten folgen in der nächsten Vorlesung

5. Parsing von Kontextfreien Sprachen

Bezüglich der Algorithmen, die sprachliche Ausdrücke erkennen können, gibt es folgende grobe Unterscheidungen:

Weitere Ausführungen folgen in der nächsten Vorlesung.

5.1 Top-Down Parsing Methoden

Weitere Ausführungen folgen in der nächsten Vorlesung.

5.2 Bottom-Up Parsing Methoden

Entsprechend der Darstellung von [SCHÖNING 2001:64ff] wurde anhand des CYK-Algorithmus ein Beispiel für einen generellen Erkennungs-Algorithmus für kontextfreie sprachen als Bottom-up Verfahren vorgestellt. Dieses Thema wird in der nächsten Vorlesung weiter vertieft werden.

6. Testfragen und Übungsaufgaben

1. Welche Anwendungsbeispiele kennen Sie aus eigener Erfahrung, in denen kontextfreie Sprachen und zugehörige Erkennungsverfahren benutzt werden?




2. Wären Sie in der Lage, zu erklären, welches Format die Normalformen CNF, GNF und EBNF haben? Wären Sie in der Lage, Beispiele für diese Formen zu konstruieren?




3. Beschreiben Sie das Prinzip eines Kellerautomaten.




4. Worin liegt der Unterschied zu einer deterministischen Turingmaschine?




5. Wie unterscheiden Sie einen Kellerautomaten von einem endlichen Automaten?




6. Wie lautet die generelle Übersetzungsvorschrift, um Zustände von Kellerautomaten in Zustandsgraphen zu übersetzen?




7. Versuchen Sie ein Beispiel eines Kellerautomaten für einfache Sprachen hinzuschreiben, z.B. die Sprachen a^*, a^*b^* und aⁿbⁿ




8. Geben Sie explizite Ableitungen für die von ihnen definierten Automaten und Sprachen an.

START