
|
|
I-RT REALZEITSYSTEME WS0304
|
Nachdem bisher das theoretische Konzept eines Systems einführend erklärt und anhand eines Beispieles illustriert worden ist, wie man Problemstellungen mit Hilfe von Systemen modellieren kann, soll ab heute der Aspekt der Zeit thematisiert werden. Das Verhalten von Systemen ist ein Vorgang in der Zeit mit vielffältigsten Implikationen. Einige wichtige Aspekte sind zu besprechen (als Hintergrundliteratur zu Thema Zeit sei speziell verwiesen auf [KOPETZ 1997]).
Bei der Behandlung von Systemen ist es nicht unbedingt notwendig, den Aspekt der Zeit zu thematisieren. Lautet aber die Aufgabenstellung so, dass das Einhalten bestimmter zeitlicher Vorgänge für die Qualität des Systems kritisch ist, dann muss man den Aspekt der Zeit von vornherein in die Betrachtung mit einbeziehen. Der grundsätzliche Zusammenhang zwischen Systemen und Zeit ergibt sich folgendermassen (siehe Bild):
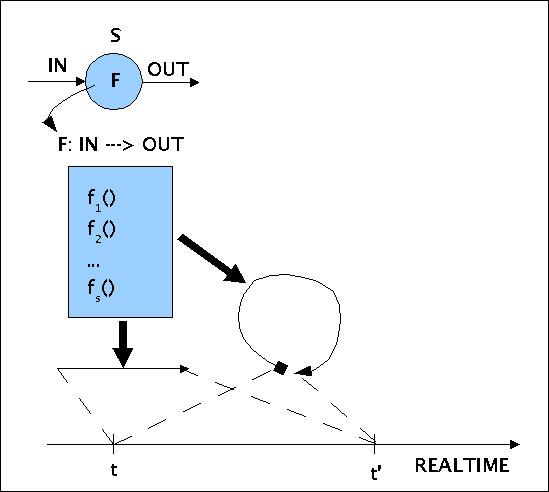
Systeme als Vorgänge in der Zeit
Theoretisch haben wir ein System S als Struktur mit Input-Output-Zuständen beschrieben, dessen Verhalten formal über die Systemfunktion F gesteuert wird. Von den Analysen her wissen wir, dass sich die Systemfunktion in der Regel in mehrere kleinere Funktionen f1(), ..., fs() zerlegen lässt. Solange wir uns im Bereich der formalen Modellierung aufhalten, gibt es 'Zeit' nur insoweit, als wir diese wiederum formal in die Systemmodellierung einbeziehen. 'Real' kommt Zeit dann ins Spiel, wenn man formale Systemmodelle auf konkreter Hardware in Form von ablauffähigen Programmen implementiert und diese Programme abarbeiten lässt. Reale Hardware (CPU, RAM, I/O-Controller usf.) benötigt immer 'reale Zeit' (Ausbreitung von elektrischen Ladungen in Leitern; Leitungslängen, Verzögerung in Bausteinen, verfügbare Taktzeiten, Synchronisation ...). Die Abarbeitung einer Teilfunktion fi() der Systemfunktion F ist in der realen Welt immer von einer 'realen Dauer' dfi, so dass die Summe aller Abarbeitungszeiten dF einer bestimmten endlichen Dauer entspricht, die sich auf eine reale Zeitmessung als ein Intervall auf der realen Zeitachse abbilden lässt. Ist die Abarbeitung einer Systemfunktion F als eine Schleife ('loop') angelegt, in der sich eine bestimmte Abfolge von Verarbeitungsschritten fi() für die Dauer der Systemtätigkeit wiederholt, dann entspricht die Gesamtheit dieser Abarbeitungsschritte leztlich auch einer endlichen Dauer mit einem entsprechenden Abschnitt auf der realen Zeitachse.
Der Output O eines Systems S als durch die Systemfunktion F bestimmte 'Antwort' auf einen bestimmten Input I
erfolgt also niemals 'direkt', sondern immer verzögert um diejenige Dauer, die durch die Abarbeitung der zu F
benötigten Abarbeitungsschritte. Sei t der Zeitpunkt eines bestimmten Inputs I und t' der Zeitpunkt einer zu I
gehörigen Antwort O aufgrund der Systemfunktion Fs von System S, dann kann man sagen dass für die
Antwortverzögerung gilt:
dFs = t' - t
Da Systeme sehr oft (meistens?) keine völlig identische Bedingungen für eine bestimmte Systemantwort haben, muss
man im allgemeinen einen sogenannten 'Jitter' unterscheiden:
jitterS = max(dFs) - min(dFs)
Bei der Planung eines zeitkritischen Systemeinsatzes ist somit der Jitter immer zu berücksichtigen; er bildet eine untere Grenze für die Genauigkeit der Prognose.
Beispiele für zeitkritische Systeme mit Jitter:
Ein alltäglich bekanntes Beispiel für einen Jitter sind die Verspätung von Nahverkehrsmittel im täglichen Personenverkehr.
Weitere prominente Beispiele sind die Reaktionszeiten beim Anwählen einer Webseite, bei der Versendung von emails oder SMS-Botschaften.
Ein anderer Bereich ist die Erzeugung digitaler Musik über die Soundkarte eines PCs oder das Abspielen von Videodaten.
Sie sitzen beim Videospiel und wundern sich über die Zeitspanne zwischen Bestätigung des Eingabegerätes und der beobachtbaren Reaktion des PCs in Bild und Ton.
Sie sitzen als Pilot in einem professionellen Flugsimulator und müssen sich auf die korrekte Anzeige der Instrumente und die korrekte Ausführung von Aktionen verlassen.
Sie sitzen in einem Kampfflugzeug und hängen davon ab, dass Ihr elektronisches Abwehrsystem in Sekundenbruchteilen Freund von Feind unterscheiden kann.
Sie liegen als PatientIn in einer Intensivstation und es sind zahlreiche medizinische Messgeräte, die einige kritische physiologische Parameter überwachen; Fehlfunktionen können für Sie tödlich enden.
In einem Logistikzentrum werden stündlich tausende von Einheiten erfasst, eingerichtet und über komplexe Transportwege 'just in time' zu bestimmten Orten transportiert; schon kleine Fehlfunktionen können sehr schnell hundertausende von Euros kosten oder gar die Existenz des Unternehmens bedrohen.
In der Flugleitzentrale eines grossen Zivilflughafens müssen Fluglotsen permanent in Sekunden Entscheidungen treffen, die hunderte von Menschenleben tangieren; die Basis ihrer Entscheidungen sind komplexe Realzeitsysteme, die eine Fülle von Daten zu aussagekräftigen Einheiten zusammenfügen um so eine Lagebeurteilung zu ermöglichen.
In den Leitzentralen grosser Energieversorger fliessen ebenfalls Unmengen von Einzeldaten zusammen, die in Realzeit geprüft und interpretiert werden müssen.
Alle grossen Finanzplätze dieser Welt operieren mittlerweile mit Realzeitsystemen, in denen im Sekundentakt Händleraktionen von tausenden von Händlern im Millionen- und Miliardenumfang getätigt werden; ein Ausfall --auch nur von kurzer Dauer-- hat riesige finanzielle Folgen.
Bisher wurde zwar schon die 'reale Zeit' erwähnt, es wurde aber noch nicht gesagt, was technisch unter 'Zeit' verstanden werden soll.
Visuell wird Zeit oft als ein gerichteter Pfeil dargestellt, auf dem man gleiche Wegstrecken abträgt und sagt, dass jeder Markierung ein 'Zeitpunkt' entsprechen soll. Doch wie ordnet man visuelle Pfeile realen Prozessen in der realen Welt zu?
Formal kann man Zeit als eine Struktur TIME darstellen mit den Forderungen:
TIME(x) gdw x = (T,<)
mit:
T ist eine Menge von Zeitpunkten
< ist eine Relation für die gilt:
(ORDNUNG DER ZEITPUNKTE)(A:t,t') (t,t' in T ==> t < t' or t = t' )
(DICHTE DER ZEITPUNKTE)(A:t,t') (t,t' in T & t < t' ==> (E:d)( t < d < t' ) )
Unter Voraussetzung einer Zeit-Struktur kann man dann die Prädikate 'vorher', 'nachher' sowie 'zur gleichen Zeit' definieren. Aber auch hier wieder die frage: wie kann man solche formalen Gebilde zu realen Prozessen in der realen Welt in Beziehung setzen?
Um diese Frage der Zuordnung von visuellen oder formalen Zeitrepräsentationen zu realen Zeitprozessen vornehmen zu können, benötigen wir einen realen Prozess in der realen Welt, mittels dem man das Konzept Zeit operationalisieren kann.
Technisch wird Zeit realisiert durch Uhren, die periodische Prozesse gleicher Länge erzeugen können und die in der Lage sind, das 'Auftreten eines solchen periodischen Ereignisses i' zu 'erkennen' und mittels eines Zählers zu zählen und anzuzeigen. Dies kann auf vielfältige Weise technisch realisiert werden. Das Auftreten eines solchen periodischen Ereignisses i einer Uhr u soll microtick von u genannt werden, geschrieben iu. Die Häufigkeit der microticks einer Uhr u pro Zeiteinheit t ist die Frequenz von u, geschrieben fu. Das Gegenstück zur Frequenz fu ist die Granularität 1/fu = gu. Die Granularität gibt die kürzeste Zeitdauer an, die mit einer Uhr u dargestellt werden kann.
Aus praktischer Sicht interessiert die Menge der Zeitpunkte vor allem deswegen, weil man bestimmten Ereignissen Zeitpunkte ('timestamps') zuordnen möchte, um dadurch sagen zu können, dass 'etwas' 'zum Zeitpunkt t' 'stattgefunden' hat.
Eine solche Zuordnung von Zeitpunkten aus einer Zeitstruktur x zu 'etwas' stellt eine Abbildung dar:
timing: E ---> Tx
wobei 'E' hier für eine beliebige Menge von benennbaren Grössen stehen soll.
t = timing(e)
würde also besagen, dass die messbare Grösse e relativ zu den Zeitpunkten ('timestamps') der Zeitstruktur x mit
dem Zeitpunkt ('timestamp') t korreliert.
Würde man auf diese Weise z.B. folgende Zuordnungen vornehmen:
t1 = timing(e1)
t2 = timing(e2)
t2 = timing(e3)
t1 < t2
dann könnte man aufgrund der zugeordneten Zeitpunkte sagen, dass Grösse e1 zeitlich vor den beiden Grössen e2 und e3 aufgetreten ist und die Grössen e2 und e3 sind zeitgleich (simultan) aufgetreten. Aufgrund solch eines zeitlichen Verhältnisses könnte man vermuten, ob zwischen dem Auftreten von Grösse e1 und den zeitlich späteren Grössen e2 und e3 möglicherweise eine kausale Beziehung besteht. Solche Überlegungen wären aber nur dann sinnvoll, wenn die zuvor vorgenommen zeitlichen Zuordnungen 'genau genug' sind. Wäre die zeitliche Zuordnung nicht genau genug, dann könnte es möglicherweise sein, dass die Grössen e2 oder e3 eventuell 'in Wirklichkeit' vor der Grösse e1 aufgetreten sind.
Das Thema der Genauigkeit von zeitlichen Zuordnungen und das Verhältnis zwischen verschiedenen Uhren soll Gegenstand einer weiteren Vorlesung sein. Hier soll nur noch angesprochen werden, welches denn nun die verbindliche Einheit für eine technische Zeitmessung ist.
Wie zuvor schon herausgearbeitet worden ist, benötigt man zur technischen Erzeugungvon regelmässigen Zeitpunkten eine Uhr u mit einer bestimmten Granularität g = 1/fu. Um aber bei verschiedenen Uhren zu einheitlichen Aussagen bzgl. der Zuordnung eines bestimmten vergleichbaren Zeitpunktes zu kommen, benötigt man eine Referenzuhr und eine Referenzzeitdauer, um jede beliebige Uhr in Beziehung zu dieser Referenzuhr setzen zu können.
Weltweit zuständig für den gültigen Zeitstandard und dessen Messung ist das Bureau International des Poids et Mesures (BIPM), das im Park de Saint-Cloud von Sèvres liegt, einem Vorort süd-westlich von Paris. Das BIPM beschreibt seine Aufgabe wie folgt:
The task of the BIPM is to ensure world-wide uniformity of measurements and their traceability to the International System of Units (SI).
It does this with the authority of the Convention of the Metre, a diplomatic treaty between fifty-one nations, and it operates through a series of Consultative Committees, whose members are the national metrology laboratories of the Member States of the Convention, and through its own laboratory work.
The BIPM carries out measurement-related research. It takes part in, and organizes, international comparisons of national measurement standards, and it carries out calibrations for Member States.
Die Existenz des BIPM geht zurück auf eine lange historische Entwicklung, deren Inhalt die immer klarere Herausarbeitung der heute benutzten internationalen Standards zur Bescheibung physikalischer Grössen ist. Hier eine kurze Geschichte der Entwicklung der internationalen Standards aus der Sicht des BIPM:
The creation of the decimal Metric System at the time of the French Revolution and the subsequent deposition of two platinum standards representing the metre and the kilogram, on 22 June 1799, in the Archives de la République in Paris can be seen as the first step in the development of the present International System of Units.
In 1832, Gauss strongly promoted the application of this Metric System, together with the second defined in astronomy, as a coherent system of units for the physical sciences. Gauss was the first to make absolute measurements of the earth's magnetic force in terms of a decimal system based on the three mechanical units millimetre, gram and second for, respectively, the quantities length, mass and time. In later years Gauss and Weber extended these measurements to include electrical phenomena.
These applications in the field of electricity and magnetism were further developed in the 1860s under the active leadership of Maxwell and Thomson through the British Association for the Advancement of Science (BAAS). They formulated the requirement for a coherent system of units with base units and derived units. In 1874 the BAAS introduced the CGS system, a three-dimensional coherent unit system based on the three mechanical units centimetre, gram and second, using prefixes ranging from micro to mega to express decimal submultiples and multiples. The following development of physics as an experimental science was largely based on this system.
The sizes of the coherent CGS units in the fields of electricity and magnetism, proved to be inconvenient so, in the 1880s, the BAAS and the International Electrical Congress, predecessor of the International Electrotechnical Commission (IEC), approved a mutually coherent set of practical units. Among them were the ohm for electrical resistance, the volt for electromotive force, and the ampere for electric current.
After the establishment of the Metre Convention on 20 May 1875 the CIPM concentrated on the construction of new prototypes taking the metre and kilogram as the base units of length and mass. In 1889 the 1st CGPM sanctioned the international prototypes for the metre and the kilogram. Together with the astronomical second as unit of time, these units constituted a three-dimensional mechanical unit system similar to the CGS system, but with the base units metre, kilogram and second.
In 1901 Giorgi showed that it is possible to combine the mechanical units of this metre-kilogram-second system with the practical electric units to form a single coherent four-dimensional system by adding to the three base units, a fourth base unit of electrical nature, such as the ampere or the ohm, and rewriting the equations occurring in electro-magnetism in the so-called rationalized form. Giorgi's proposal opened the path to a number of new developments.
After the revision of the Metre Convention by the 6th CGPM in 1921, which extended the scope and responsibilities of the BIPM to other fields in physics, and the subsequent creation of the CCE (now CCEM) by the 7th CGPM in 1927, the Giorgi proposal was thoroughly discussed by the IEC and the IUPAP and other international organizations. This led the CCE to recommend, in 1939, the adoption of a four-dimensional system based on the metre, kilogram, second and ampere, a proposal approved by the ClPM in 1946.
Following an international inquiry by the BIPM, which began in 1948, the 10th CGPM, in 1954, approved the introduction of the ampere, the kelvin and the candela as base units, respectively, for electric current, thermodynamic temperature and luminous intensity. The name International System of Units (SI) was given to the system by the 11th CGPM in 1960. At the 14th CGPM in 1971 the current version of the SI was completed by adding the mole as base unit for amount of substance, bringing the total number of base units to seven.
Wichtig ist, dass das internatinale System der Standards kein statisches System ist, sondern sich entsprechend den technischen Bedürfnissen dynamisch weiterentwickelt.
Die aktuelle Tafel der Basiseinheit nach der Darstellung des BIPM lautet wie folgt:
|
Quantity |
Unit |
Definition |
|
|
metre |
m |
The metre is the length of the path travelled by light in vacuum during a time interval of |
|
|
kilogram |
kg |
The kilogram is the unit of mass; it is equal to the mass of the international prototype of the kilogram. |
|
|
second |
s |
The second is the duration of |
|
|
ampere |
A |
The ampere is that constant current which, if maintained in two straight parallel conductors of infinite length, of negligible circular cross-section, and placed |
|
|
kelvin |
K |
The kelvin, unit of thermodynamic temperature, is the fraction 1/273.16 of the thermodynamic temperature of the triple point of water. |
|
|
mole |
mol |
The mole is the amount of substance of a system which contains as many elementary
entities as there are atoms in | |
|
candela |
cd |
The candela is the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency |
Damit ist nun klar, dass die internationale Masseinheit für die Zeit die Sekunde ist und dass die Referenzuhr für
die Messung einer Sekunde eine Uhr ist, die auf periodischen Prozessen im Cäsium-Atom beruht, d.h.
Frequenz einer Cäsium-basierten Atomuhr: fcs = 9.192.631.770 pro sec
Granularität einer Cäsium-basierten Atomuhr: gcs = 1/9.192.631.770 sec
Eine gute prinzipielle Beschreibung einer Cäsium-basierten Atomuhr" findet sich auf der Seite von Herget:
"Atomic clocks work on the following principle: Atoms occur in different energy states one of which is identified by the symbol (+) and one by the symbol (-). The transition of an atom from the (+) to the (-) state can be stimulated and is connected with the emission of electromagnetic radiation of a characteristic frequency. In the case of the caesium atom, this frequency, fcs has a value of 9.192.631.770 Hz, corresponding to an oscillation period of (1 / 9.192.631.770) seconds. According to the laws of atomic physics, fcs is equal to the energy difference between the (+) and (-) states divided by the Planck constant h. For the caesium atom in particular, the constancy in time of fcs much better than that of, for example, the oscillation period of a pendulum, the oscillation frequency of a quartz or the rotation period of the earth."
"Caesium atoms are evaporated in the vacuum chamber of an atomic clock. The magnet arranged behind the oven separates the atoms such that only atoms in the (+) state enter the cavity resonator. Here exposure to a microwave field stimulates the atoms to pass into the (-) state. The second magnet then directs to the detector only these atoms. The number of atoms at the collector reaches a maximum when the frequency of the irradiation field has the value fcs. A feedback circuit ensures that the microwave oscillator Q is kept at the frequency fcs. By the counting of 9.192.631.770 periods, the time interval of one second is obtained from the oscillator signal."
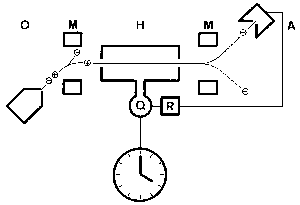 | Diagram of an atomic clock: | |||
| O | atomic bem oven | Q | microwave oscillator | |
|---|---|---|---|---|
| M | sorting magnet | A | detector | |
| H | cavity resonator | R | servo control circuit | |
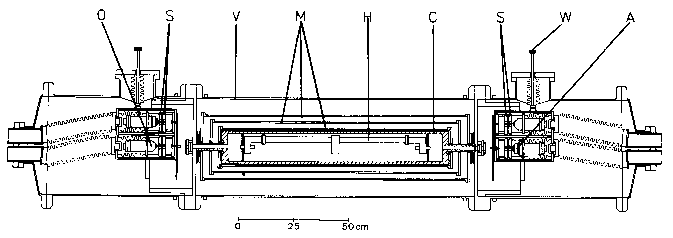
| Horizontal section through the CS2 primary time and frequency standard of the PTB | |||
| O | caesium beam oven | S | sorting magnets |
|---|---|---|---|
| V | vacuum recipient | M | mu-metal shields |
| H | cavity resonator | W | beam reversal manipulator |
| C | coil to generate a homogeneous magnatic field (C-field) | A | detector |
Selbst wenn man jetzt mit der Einheit 'sec' einen einheitlichen Standard für die Messung der Zeit hat, reicht dies alleine noch nicht aus, um Zeit weltweit einheitlich zu messen. Das Schweizerische Bundesamtes für Metrologie und Akkreditierung (METAS) gibt einen guten Überblick über die wichtigsten Zeitskalen , die international benutzt werden:
|
Definition der gebräuchlichsten Zeitskalen
|
Berücksichtigt man die Zeit, dann kann man das Verhalten von Systemen mit speziellen Begriffen beschreiben. Einige wichtige seien hier angeführt.
6.1. Zuverlässigkeit ('reliability')
Der erste Begriff --Zuverlässigkeit ('reliability')-- hat zu tun mit der Wahrscheinlichkeit, mit der nach einem Fehler zu einem Zeitpunkt t0 zu einem späteren Zeitpunkt t wieder ein Fehler auftreten wird. Sei lambda die Anzahl der Fehler pro Stunde (Fehlerrate, 'failurrate'), dann gilt die Formel:
zuv(t,t0,lambda) = exp(-lambda(t-t0)) (wobei t - t0 in Stunden gezählt wird)
Die Grösse MTTF (:= mean time to failure) wird wie folgt definiert:
MTTF = 1/lambda
Ein Webserver, der 1x pro Woche ausfällt hätte also die Werte:
1 Woche = 24h * 7 = 168h
lambda = 1/168 = 0.0059524
MTTF = 1/lambda = 168h
zuv(168,1,lambda) = 0.3700757
6.2. Wartbarkeit ('maintainability')
Wartbarkeit hat damit zu tun, wieviel Zeit man benötigt, um ein System nach dem Auftreten eines Fehlers wieder in einen betriebsfähigen Zustand zu versetzen. Ein hier vielfach benutzter Begriff ist der Begriff Mittlere Zeit zur Wiederherstellung ('Mean Time to Repair', MTTR). Setzt man eine konstante Reparaturrate my an (Reparaturen pro Stunde), dann kann man --analog zu MTTF-- vereinbaren: MTTR = 1/my.
6.3. Verfügbarkeit ('availability')
Verfügbarkeit beschreibt die Zeit, in der ein Dienst verfügbar ist (MTTF) im Verhältnis zur Zeit in der er wegen Reparatur nicht verfügbar ist (MTTR) und verfügbar ist (MTTF), also MTTR+MTTF. Im Falle konstanter Fehler- und Reparaturraten gilt dann:
A = MTTF/(MTTF+MTTR)
mit A := AVAILABILITY.
Ferner gilt:
MTBF = MTTF+MTTR
(MTBF := Mean Time Before Failure, Mittlere Zeit vor dem nächsten Fehler), das ergibt:
A = MTTF/MTBF
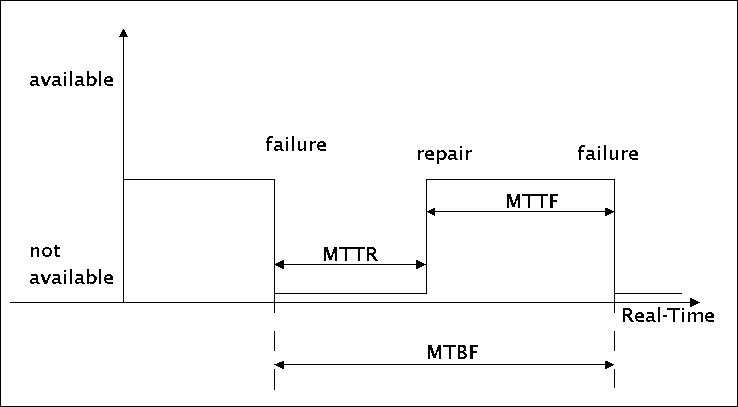
Fälle von Verfügbarkeit
Für die Klassifikation von Realzeit-Systemen stehen zahlreiche Kategorien zur Verfügung. Einige seien hier aufgelistet:
Fail-safe/Fail-operational: In einem System, das 'fail-safe' ist, kann das System mit hoher Wahrscheinlichkeit einen Fehler erkennen und dann einen sicheren Zustand ansteuern. In Situationen, in denen keine sicheren Zustände verfügbar sind, ist das System 'fail-operational'.
Guaranteed-Response/ Best-Effort: eine garantierte Antwort ('guaranteed-response') liegt vor, wenn ein System so umfassend analysiert worden ist, dass es in allen voraussagbaren Belastungssituationen eine definierte Antwort zu geben vermag. Ist eine umfassende Analyse nicht verfügbar, dann kann es nur 'beste Versuche' ('best effort') geben, eine Antwort bereitzustellen; dies kann mangelhaft sein.
Resource-Adequate/ Resource Inadequate: in einem ressourcenadäquaten System stehen in allen Belastungsfällen genügend Ressourcen zur Verfügung. In vielen Systemen wird aber aus Wirtschaftlichkeitsüberlegungen mit limitierten Ressourcen gearbeitet, die aufgrund von Wahrscheinlichkeitsüberlegungen dynamisch verwaltet werden. Bei schlechten Einschätzungen sind damit Störfälle wahrscheinlich.
Event-triggered/ Time-triggered: in ereignisgetriebenen ('event triggered') Systemen reagiert ein System ausschliesslich auf das Auftreten bestimmter Ereignisse, die durch sogenannte Unterbrechungen ('interrupts') 'bekannt' werden. Das System muss dann dynamisch auf diese Unterbrechungen reagieren. Im Unterschied dazu orientieren sich zeitgetriebene ('time triggered') Systeme ausschliesslich an einem Systemtakt ('system clock'), der fest mit bestimmten Aktionen verknüpft ist. In verteilten Systemen stellt dabei die Synchronisation der verschiedenen Systemtakte eine wichtige Aufgabe dar (siehe oben)..
Hard Real-Time/ Soft Real-Time: der zentrale Unterschied zwischen Hard Realtime Systemen und Soft Realtime Systemen kann wohl am besten am Verhältnis zur Umwelt festgemacht werden. Ein hartes Realzeit-System muss absolut synchron bleiben mit den Ereignissen in seiner Umgebung, wohingegen ein weiches Realzeit-System seine Antwortzeiten unter Belastung bis zu einem gewissen Grad gegenüber der Umgebung verlangsamen kann (z.B. dauern die Reaktionszeiten eines Servers im Netz dann einfach länger) ohne dabei Schaden anzurichten. Die Zeitanforderungen von harten Realzeit-Systemen liegen auch oft in kleineren Zeiteinheiten (Milisekunden und weniger) als bei weichen Realzeitsystemen (Sekunden). Damit harte Realzeit-Systeme ihre Leistungen zuverlässig erbringen können, müssen sämtliche Belastungssituationen, auch die eher seltenen, vollständig analysiert sein, so dass eine garantierte Antwort gewährleistet wird. Bei weichen Systemen reicht in der Regel eine durchschnittliche Antwortzeit. Ferner verlangen harte Realzeit-Systeme eine sehr zuverlässige autonome Fehlererkennung und Fehlerbehandlung innerhalb klar definierter zeitlicher Grenzen. Für harte Realzeit-Systeme ist es ferner wichtig, dass ihre zeitlichen Daten innerhalb sehr enger Grenzen absolut zuverlässig sind; die impliziert, dass es sich um kleine Datensätze handelt. Demgegenüber operieren viele weiche Realzeit-Systeme mit grossen Datensätzen, deren Integrität über lange Zeiträume zu gewährleisten ist. Roll-Back-Strategien weicher Realzeit-Systeme sind wegen der sehr engen zeitlichen Schranken für harte Realzeitsysteme in der Regel nicht anwendbar.
Warum brauchen Systeme für ihre Antworten auf bestimmte Eingaben Zeit?
Was ist der Jitter eines Systems und wie ist er definiert?
Geben Sie Beispiele von Systemen mit Jitter.
Was ist Zeit im Bereich technischer Systeme?
Wie kann man Zeit messen?
Was ist eine Uhr?
Wie ist heute die Basiseinheit für Zeit definiert?
Wofür benötigt man 'kleine' Zeiteinheiten?
Was bedeuten UT0, UT1, TAI und UTC? Wie hängen sie untereinander zusammen?
Was bedeuten die Kürzel MTTR, MTTF, MTBF?
Was versteht man unter der Zuverlässigkeit, Wartbarkeit und Verfügbarkeit von Systemen?
Beschreiben Sie die wichtigen Eigenschaften von fünf wichtigen Klassifikationen von Realzeitsystemen.
Geben Sie 7 Beispiele von Realzeitsystemen aus ihrer alltäglichen Umgebung an und geben sie Erfahrungswerte an für MTTF, MTTR und Zuverlässigkeit dieser Systeme.
Geben Sie 3 Beispiele von Realzeitsystemen aus ihrer alltäglichen Umgebung, deren Zuverlässigkeit ihrer Einschätzung nach vergleichsweise am höchsten liegen und 3 Beispiele von Realzeitsystemen, deren Zuverlässigkeit vergleichsweise am niedrigsten liegen.