
|
|
I-ALGO SS03 - ALGORITHMS AND DATASTRUCTURES - Lecture with Exercises
|
In the preceding lecture an overview about graphs with different kinds of properties has been presented. In the exercises You have been invited to construct some example graphs, to make proposals for datastructures and to define algorithms for some problems. In this lecture we will give concrete examples for datastructures and for three algorithms. The concrete examples are realized in C++ and are mostly taken from the webpage related to the book [WEISS 2001], which is listed in the literature in the head of this course. The examples have been simplified to meet the conditions of this lecture.
To represent the structure of an graph in a computer there are mainly three strategies to do this:
Adjacency Matrix
Adjacency List (with vectors or lists)
Adjacency List (with double connected lists)
We will examine in the following a solution, which is using an adjacency list realized by a map where every vertex X has a vector with those vertices as elements which are direct successors of the vertex X in the map, i.e. those vertices which are 'adjacent' to X.
To start with the computer processing of graphs one has to present a computer-readable form of a graph. This is done by using an editor for a textfile which follows some simple syntax in writing the representations of graphs. Let us assume we have the following simple positively weighted directed graph g1:
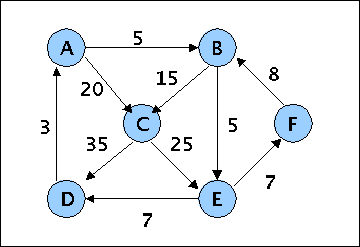
A positively weighted directed graph g1
A simple syntax to represent this graph g1 in a textual form could be the following one:
A B 5 A C 20 B C 15 B E 5 C D 35 C E 25 D A 3 E D 7 E F 7 F B 8
To process these data it would be necessary to read this file, organize it into a convenient data-structure and then to apply several algorithms.
The following small program reads a datafile with the specification of a graph and sets up the appropriate data-structures. Then it asks the user, which kind of algorithm for shortest path her wants to apply. Three options are in this version available: unweighted, negative and acyclic.
The include files used are:
#include <climits> #include <cstdlib> #include <fstream> #include <iostream> #include <map> #include <vector> #include <string> #include <queue> #include <functional> #include <list> #include <sstream>
// A simple main that reads the file given by argv[1]
// and then calls processRequest to compute shortest paths.
// Skimpy error checking in order to concentrate on the basics.
int main( int argc, char *argv[ ] )
{
Graph g;
if( argc != 2 )
{
cerr << "Usage: " << argv[ 0 ] << " graphfile" << endl;
return 1;
}
ifstream inFile( argv[ 1 ] );
if( !inFile )
{
cerr << "Cannot open " << argv[ 1 ] <<
endl;
return 1;
}
cout << "Reading file... " << endl;
string oneLine;
// Read the edges; add them to g
while( getline( inFile, oneLine) )
{
string source, dest;
double cost;
cout << "TEST: " << oneLine << endl;
istringstream st( oneLine );
st >> source; st >> dest; st >> cost;
if( st.fail( ) )
cerr << "Bad line: " << oneLine << endl;
else
g.addEdge( source, dest, cost );
}
cout << "File read" << endl << endl;
while( processRequest( cin, g ) )
;
return 0;
}
// Process a request; return false if end of file.
bool processRequest( istream & in, Graph & g )
{
string startName;
string destName;
char alg;
cout << "CONTINUE (y/n) ?: ";
if( !( in >> startName ) )
return false;
else if (startName == "n") return false;
cout << "Enter start node: ";
if( !( in >> startName ) )
return false;
cout << "Enter destination node: ";
if( !( in >> destName ) )
return false;
cout << "Enter algorithm (u, n, a): ";
in >> alg;
if( alg == 'u' ){
g.unweighted( startName );
}
else if( alg == 'n' ){
g.negative( startName );
}
else if( alg == 'a' ){
g.acyclic( startName );
}
g.printPath( destName );
return true;
}
The before mentioned program instantiates an object g of type 'class graph', reads the specifications of a graph and sets up a datastructure for the object g by using the elementfunction g.addEdge( source, dest, cost );.
The definition of the class graph runs as follows:
// Graph class interface: evaluate shortest paths.
//
// CONSTRUCTION: with no parameters.
//
// ******************PUBLIC OPERATIONS**********************
// void addEdge( string v, string w, double cvw )
// --> Add additional edge
// void printPath( string w ) --> Print path after alg is run
// void unweighted( string s ) --> Single-source unweighted
// void negative( string s ) --> Single-source negative weighted
// void acyclic( string s ) --> Single-source acyclic
// ******************ERRORS*********************************
// Some error checking is performed to make sure graph is ok,
// and to make sure graph satisfies properties needed by each
// algorithm.
// Gerd D-H added some control-functions for demonstrations during
// lecture
class Graph
{
public:
Graph( ) { }
~Graph( );
void addEdge( const string &
sourceName, const string & destName, double cost );
void printPath( const string &
destName ) const;
void unweighted( const string & startName );
void negative( const string & startName );
void acyclic( const string &
startName );
private:
Vertex * getVertex( const string & vertexName );
void printPath( const Vertex &
dest ) const;
void printName( const Vertex *
target ) const; //added by gerd d-h
void clearAll( );
typedef map<string,Vertex *,less<string> > vmap;
// Copy semantics are disabled; these make no sense.
Graph( const Graph & rhs ) {
}
const Graph & operator= ( const Graph & rhs ) { return *this; } vmap
vertexMap; };
One of the interesting points here is the fact, that no special constructor-function is defined, but a special deconstructor-function. The reason why is that this class uses --within the functions addEdge() and getVertex()-- datastructures based on pointers. To remove those datastructures cleanly one needs a special destructor which deletes all the pointer-based memory-space.
Another interesting point is the blocking of the copy-constructors by declaring them private!
Now the question has to be answered how the internal datastructurs look like which are used to represent a graph.
One hint is given in the class-definition directly where the object
vmap vertexMap;
is introduced. The type 'vmap' is an abbreviation of :
typedef map<string,Vertex *,less<string> > vmap;
this is the datatype 'map' with the type 'string' for the key and the type 'Vertex' for the value. The ordering relation is 'less' defined between strings. With such a map --which is internally organized as a binary search tree (mostly as a Red-Black-Tree)-- one can search for names of vertices and one will then get a uniquely identifying address which leads to a vertex (see below).
That function which finally creates concrete vertices and edges by using the before mentioned map is the function addEdge(...source, ...destination, ...cost) which internally is calling the function getVertex(). Realizing the function addEdge() one needs the data types 'Vertex' and 'Edge'.
// Add a new edge to the graph.
void Graph::addEdge( const string & sourceName, const string &
destName, double cost ) { Vertex * v =
getVertex( sourceName ); Vertex * w = getVertex( destName ); v->adj.push_back(
Edge( w, cost ) ); }
// If vertexName is not present, add it to vertexMap.
// In either case, return (a pointer to) the Vertex.
Vertex * Graph::getVertex( const string & vertexName )
{
vmap::iterator itr = vertexMap.find( vertexName );
if( itr == vertexMap.end( ) )
{
Vertex *newv = new Vertex( vertexName );
vertexMap[ vertexName ] = newv;
return newv;
}
return (*itr).second;
}
As everybody can see from the following example are the definitions of 'Edge' and 'Vertex' mutually dependent, i.e. to define e.g. 'Edge' you need 'Vertex' as already to be defined and vice versa. So solve this problem of a simultaneous definition one introduces one of the datastructures as a 'dummy' structure by giving only the name, then one defines the other one explicitly and then one defines the dummy-term explicitly by using the before-introduced other term.
Edge is defined as a struct --or: as an weakened class-- containing the address of the goal-vertex without the first vertex, because the edge is inserted in the adjacency list of the first vertex.
struct Vertex;
struct Edge
{
// First vertex in edge is implicit
Vertex *dest; // Second vertex in edge
double cost; // Edge cost
Edge( Vertex *d = 0, double c =
0.0 )
: dest( d ), cost( c ) { }
};
// Basic info for each vertex.
struct Vertex
{
string name; // Vertex name
vector<Edge> adj; // Adjacent vertices (and costs)
double dist; // Cost
Vertex *prev; // Previous vertex on shortest path
int scratch; // Extra variable used in algorithm
Vertex( const string & nm ) : name( nm )
{ reset( ); }
void reset( )
{ dist = INT_MAX; prev = NULL; scratch = 0; }
};
Putting all these information together we get the following unifying view: The function addEdge() is calling for every vertex-name the function getVertex( const string & vertexName ) which reads the name of a vertex --e.g. 'A'--, creates a new object of type vertex with a unique address and inserts this address as a value to the key 'A'. Thus the search to the name 'A' will then lead by the value (:= address) to the vertex-object connected to the name 'A'.

The datastructure map pointing to vertices containing adjacency vectors
Every vertex manages then its own list of adjacent vertices with the aid of a vector-object whose elements are of type 'edge'. Such an edge-element consists of the address of the next ('adjacent') vertex to which an edge 'points to' as well as the costs to reach this vertex. The vertex 'A' of the example-graph g1 has two destinations: vertex 'B' and vertex 'C'. Vertex 'B' has the cost '5' and vertex 'C' the cost '20'. The 'distance'-element has as an initial value the value 'INT_MAX' of the host machine and the 'scratch'-element has as initial value the value '0'.
Ater having read a graph-specification file programramm will have set up the internal structure of this graph by calling repeatedly the function addEdge() which in turn is calling getVertex(). The data are ready to get processed by some graph-specific algorithm. In the following we will show three different algorithms applicable to the before explained data-structures.
// Driver routine to handle unreachables and print total cost.
// It calls recursive routine to print shortest path to
// destNode after a shortest path algorithm has run.
void Graph::printPath( const string
& destName ) const
{
vmap::const_iterator itr = vertexMap.find( destName );
if( itr == vertexMap.end( ) ){
cerr << "Destination vertex not found" << endl;
break;
}
const Vertex & w = *(*itr).second;
if( w.dist == INT_MAX )
cout << destName << " is unreachable";
else
{
cout << "(Cost is: " << w.dist << ") ";
printPath( w );
}
cout << endl;
}
// Recursive routine to print shortest path to dest
// after running shortest path algorithm. The path
// is known to exist.
void Graph::printPath( const Vertex
& dest ) const
{
if( dest.prev != NULL )
{
printPath( *dest.prev );
cout << " to ";
}
cout << dest.name;
}
Please note the recursive structure of the function printPath( const Vertex & dest ) const!
// Initialize the vertex output info prior to running
// any shortest path algorithm.
void Graph::clearAll( )
{
for( vmap::iterator itr = vertexMap.begin( ); itr !=
vertexMap.end( ); ++itr )
(*itr).second->reset( );
}
// Print the name of Address
// By gerd d-h
void Graph::printName( const Vertex *
target ) const
{
cout << "ACTIVE VERTEX = " << target->name << endl;
}
Now, after having prepared some routines to read graph-specifications from a file and representing these in some data-structures, one can define and implement some algorithms, to operate on these structures.
As one can imagine from the preceding general descriptions of graphs there is a great number of variants resulting from the combinatorial richness of graph-types. In the following we will show explicitly three algorithms for shortest path and implicitly one algorithm for topological sort.
The systematic can be explained by the following table:
This table shows in the first column the name of a problem and in the following columns you can find some of the possible basic attributes of a graph. The same problem can get quite different solutions if the attributes of the graph are changing.
|
Table of some Graph-Algorithms |
|||||
|
PROBLEM |
+/- DIR |
+/- CYCL |
- WEIGHTED |
+ WEIGHTED |
|
|
+ POS.WEIGHTED |
+ NEG.WEIGHTED |
||||
|
Topological Sort |
+ DIR |
- CYCL |
--- |
--- |
--- |
|
Shortest Path |
+ DIR |
+ CYCL |
+++ |
--- |
--- |
|
Shortest Path |
+ DIR |
+ CYCL |
--- |
+++ |
+++ |
|
Shortest Path |
+ DIR |
- CYCL |
--- |
--- |
+++ |
In dealing with these problems one should in the 'ideal case' follow the following steps to investigate the problem:
What is the general idea of the problem?
Give a formal description of the problem
Give a formal description of the solution
Prove the correctness of the formal solution
Prove the completeness of the formal solution
Implement the formal solution as algorithm
Show the efficiency of the implementation
The 'ideal case' would require to give a detailed formal description of the problem to be able to prove in the strict sense the corectness and completeness of an algorithm. Because this cannot be afforded under the conditions of our course we have to limit ourselves to 'principal considerations' related to the nature of the problem and general conditions to solve it. Thus we will turn the ideal case in the following 'practical format':
Informal description of the problem?
Formal description of the solution as algorithm (using pseudo-code, structured programming, C++-Code)
Consider correctness and completeness of the algorithm related to the problem
Show the efficiency of the implementation related to memory and time
|
Table of some Graph-Algorithms |
|||||
|
PROBLEM |
+/- DIR |
+/- CYCL |
- WEIGHTED |
+ WEIGHTED |
|
|
+ POS.WEIGHTED |
+ NEG.WEIGHTED |
||||
|
Shortest Path |
+ DIR |
+ CYCL |
+++ |
--- |
--- |
6.1.1 Informal description of the problem
Given a directed cyclic unweighted graph. Select an arbitrary vertex for start. Search for the shortest possible path.
Remark 1: if one takes an unweighted graph as a special case of a weighted graph, then are the 'weights' in an unweighted graph all set to 1. Alternatively one can define a graph without any weights! Here we assume an unweighted graph to be a weighted graph with all weights equal to 1.
Remark 2: The algorithm should search for all possible paths, but show then only the shortest one with the goal given by the user.
6.1.2 Formal description of the solution (using pseudo-code, structured programming, C++-Code)
Considering correctness and completeness
One possible idea to solve the problem is to start with the start-vertex and then search all successors. Then search all successors of the successors, and so on, until there is no vertex left to search for.
Setting the field 'distance' of each vertex at the beginning to INT_MAX (as 'infinite') and the field 'predecessor' to NULL, one can start with the start vertex giving the distance-field the values 0. Every successor will then be incremented by 1 as long as the successor has still the value INT_MAX showing that he has not yet been visited. The field 'predecessor' of the updated vertex will then be set to the vertex for which it was a successor.
This procedures guarantees the following properties:
ALL possible successord will be visited
EVERY vertex will be visited ONLY ONCE
// Single-source unweighted shortest-path algorithm.
void Graph::unweighted( const string
& startName )
{
vmap::iterator itr = vertexMap.find( startName );
if( itr == vertexMap.end( ) ) {
cerr << " startName is not a vertex in this graph" << endl;
return;
}
clearAll( );
Vertex *start = (*itr).second;
list<Vertex *> q;
q.push_back( start ); start->dist = 0;
printName( (*itr).second ); //Control
while( !q.empty( ) )
{
Vertex *v = q.front( ); q.pop_front( );
for( int i = 0; i < v->adj.size( ); i++ )
{
Edge e = v->adj[ i ];
Vertex *w = e.dest;
if( w->dist == INT_MAX )
{
printName( e.dest ); //Control
w->dist = v->dist + 1;
cout << "ACTUAL DISTANCE = " << w->dist << endl; //Control
w->prev = v;
q.push_back( w );
}
}
}
}
Here is an example of one run with this algorithm:
gerd@goedel:~/WEB-MATERIAL/fh/I-ALGO/I-ALGO-EX/EX7/G0> ./g1 g1.txt Reading file... TEST: A B 5 TEST: A C 20 TEST: B C 15 TEST: B E 5 TEST: C D 35 TEST: C E 25 TEST: D A 3 TEST: E D 7 TEST: E F 7 TEST: F B 8 File read CONTINUE (y/n) ?: y Enter start node: F Enter destination node: D Enter algorithm (u, n, a): u ACTIVE VERTEX = F ACTIVE VERTEX = B ACTUAL DISTANCE = 1 ACTIVE VERTEX = C ACTUAL DISTANCE = 2 ACTIVE VERTEX = E ACTUAL DISTANCE = 2 ACTIVE VERTEX = D ACTUAL DISTANCE = 3 ACTIVE VERTEX = A ACTUAL DISTANCE = 4 (Cost is: 3) F to B to C to D CONTINUE (y/n) ?: n
6.1.3 Show the efficiency of the implementation related to memory and time
See exercises.
|
Table of some Graph-Algorithms |
|||||
|
PROBLEM |
+/- DIR |
+/- CYCL |
- WEIGHTED |
WEIGHTED |
|
|
POS.WEIGHTED |
NEG.WEIGHTED |
||||
|
Shortest Path |
+ DIR |
+ CYCL |
--- |
+++ |
+++ |
6.2.1 Informal description of the problem
Given a directed cyclic negative-weighted graph. Select an arbitrary vertex for start. Search for the shortest possible path.
Remark: The algorithm should search for all possible paths, but show then only the shortest one with the goal given by the user.
6.2.2 Formal description of the solution (using pseudo-code, structured programming, C++-Code)
Considering correctness and completeness
A first idea to solve the problem is to start with the start-vertex and then search all successors. Then search all successors of the successors, and so on, until there is no vertex left to search for. But because in the case of negative costs the value of whole path can be changed completely compared to other alternative paths one can not built the algorithm as straightforward than before in the case of an unweighted graph. This means, one has to allow not only to follow the 'spatial' shortest path but to consider more 'complex' patterns. Analyzing these more 'complex' paths reveals then, that there can arise 'negative cost cycles' which can only be 'stopped' by a formal argument like 'maximal number of visits'.
Therefore does this procedures NOT guarantee to find in any case a shortest possible path, not only a path at all. But what one should try to prove is that if there is a solution at all, then the algorithm will find that one.
// Single-source negative weighted shortest-path algorithm.
void Graph::negative( const string
& startName )
{
vmap::iterator itr = vertexMap.find( startName );
if( itr == vertexMap.end( ) ){
cerr << "GraphException: startName is not a vertex in this graph" << endl;
return;
}
clearAll( );
Vertex *start = (*itr).second;
list<Vertex *> q;
q.push_back( start ); start->dist = 0; start->scratch++;
printName((*itr).second ); //Control
cout << "ACTUAL SCRATCH = " << start->scratch << endl; //Control
while( !q.empty( ) )
{
Vertex *v = q.front( ); q.pop_front( );
if( v->scratch++ > 2 * vertexMap.size( ) ){
cout << "ACTUAL SCRATCH BEFORE EXCEPTION = " << v->scratch << endl;
//Control
cerr << "GraphException: Negative cycle detected" << endl;
return;
}
for( int i = 0; i < v->adj.size( ); i++ )
{
Edge e = v->adj[ i ];
Vertex *w = e.dest;
cout << "SUCC: "; printName( e.dest ); //Control
double cvw = e.cost;
cout << "SUCC COSTS = " << cvw << endl; //Control
if( w->dist > v->dist + cvw )
{
w->dist = v->dist + cvw;
cout << "INCREASED SUM-COSTS = " << w->dist << endl;
//Control
w->prev = v;
cout << "SCRATCH BEFORE = " << w->scratch << endl;
//Control
// Enqueue only if not already on the queue
if( w->scratch++ % 2 == 0 ){
cout << "INCREASED SCRATCH = " << w->scratch << endl;
//Control
q.push_back( w );
}
else {
w->scratch--; // undo the push
cout << "DECREASED SCRATCH = " << w->scratch << endl;
//Control
}
}
}
}
}
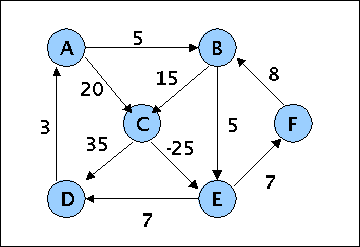
A negativ-weighted directed graph g1
gerd@goedel:~/WEB-MATERIAL/fh/I-ALGO/I-ALGO-EX/EX7/G0> ./g1 g2.txt Reading file... TEST: A B 5 TEST: A C 20 TEST: B C 15 TEST: B E 5 TEST: C D 35 TEST: C E -25 TEST: D A 3 TEST: E D 7 TEST: E F 7 TEST: F B 8 File read CONTINUE (y/n) ?: y Enter start node: F Enter destination node: D Enter algorithm (u, n, a): n ACTIVE VERTEX = F ACTUAL SCRATCH = 1 SUCC: ACTIVE VERTEX = B SUCC COSTS = 8 INCREASED SUM-COSTS = 8 SCRATCH BEFORE = 0 INCREASED SCRATCH = 1 SUCC: ACTIVE VERTEX = C SUCC COSTS = 15 INCREASED SUM-COSTS = 23 SCRATCH BEFORE = 0 INCREASED SCRATCH = 1 SUCC: ACTIVE VERTEX = E SUCC COSTS = 5 INCREASED SUM-COSTS = 13 SCRATCH BEFORE = 0 INCREASED SCRATCH = 1 SUCC: ACTIVE VERTEX = D SUCC COSTS = 35 INCREASED SUM-COSTS = 58 SCRATCH BEFORE = 0 INCREASED SCRATCH = 1 SUCC: ACTIVE VERTEX = E SUCC COSTS = -25 INCREASED SUM-COSTS = -2 SCRATCH BEFORE = 1 DECREASED SCRATCH = 1 SUCC: ACTIVE VERTEX = D SUCC COSTS = 7 INCREASED SUM-COSTS = 5 SCRATCH BEFORE = 1 DECREASED SCRATCH = 1 SUCC: ACTIVE VERTEX = F SUCC COSTS = 7 SUCC: ACTIVE VERTEX = A SUCC COSTS = 3 INCREASED SUM-COSTS = 8 SCRATCH BEFORE = 0 INCREASED SCRATCH = 1 SUCC: ACTIVE VERTEX = B SUCC COSTS = 5 SUCC: ACTIVE VERTEX = C SUCC COSTS = 20 (Cost is: 5) F to B to C to E to D CONTINUE (y/n) ?: n gerd@goedel:~/WEB-MATERIAL/fh/I-ALGO/I-ALGO-EX/EX7/G0>
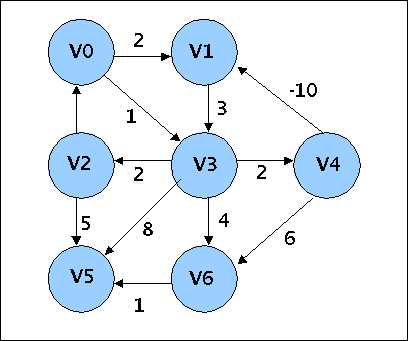
A negativ-weighted directed graph graph2
gerd@goedel:~/WEB-MATERIAL/fh/I-ALGO/I-ALGO-EX/EX7/G0> ./g1 graph2.txt Reading file... TEST: V0 V1 2 TEST: V0 V3 1 TEST: V1 V3 3 TEST: V3 V2 2 TEST: V3 V4 2 TEST: V3 V5 8 TEST: V3 V6 4 TEST: V2 V0 4 TEST: V2 V5 5 TEST: V4 V1 -10 TEST: V4 V6 6 TEST: V6 V5 1 TEST: Bad line: File read CONTINUE (y/n) ?: y Enter start node: V0 Enter destination node: V6 Enter algorithm (u, n, a): n ACTIVE VERTEX = V0 ACTUAL SCRATCH = 1 SUCC: ACTIVE VERTEX = V1 SUCC COSTS = 2 INCREASED SUM-COSTS = 2 SCRATCH BEFORE = 0 INCREASED SCRATCH = 1 SUCC: ACTIVE VERTEX = V3 SUCC COSTS = 1 INCREASED SUM-COSTS = 1 SCRATCH BEFORE = 0 INCREASED SCRATCH = 1 SUCC: ACTIVE VERTEX = V3 SUCC COSTS = 3 SUCC: ACTIVE VERTEX = V2 SUCC COSTS = 2 INCREASED SUM-COSTS = 3 SCRATCH BEFORE = 0 INCREASED SCRATCH = 1 SUCC: ACTIVE VERTEX = V4 SUCC COSTS = 2 INCREASED SUM-COSTS = 3 SCRATCH BEFORE = 0 INCREASED SCRATCH = 1 SUCC: ACTIVE VERTEX = V5 SUCC COSTS = 8 INCREASED SUM-COSTS = 9 SCRATCH BEFORE = 0 INCREASED SCRATCH = 1 SUCC: ACTIVE VERTEX = V6 SUCC COSTS = 4 INCREASED SUM-COSTS = 5 SCRATCH BEFORE = 0 INCREASED SCRATCH = 1 SUCC: ACTIVE VERTEX = V0 SUCC COSTS = 4 SUCC: ACTIVE VERTEX = V5 SUCC COSTS = 5 INCREASED SUM-COSTS = 8 SCRATCH BEFORE = 1 DECREASED SCRATCH = 1 SUCC: ACTIVE VERTEX = V1 SUCC COSTS = -10 INCREASED SUM-COSTS = -7 SCRATCH BEFORE = 2 INCREASED SCRATCH = 3 SUCC: ACTIVE VERTEX = V6 SUCC COSTS = 6 SUCC: ACTIVE VERTEX = V5 SUCC COSTS = 1 INCREASED SUM-COSTS = 6 SCRATCH BEFORE = 2 INCREASED SCRATCH = 3 SUCC: ACTIVE VERTEX = V3 SUCC COSTS = 3 INCREASED SUM-COSTS = -4 SCRATCH BEFORE = 2 INCREASED SCRATCH = 3 SUCC: ACTIVE VERTEX = V2 SUCC COSTS = 2 INCREASED SUM-COSTS = -2 SCRATCH BEFORE = 2 INCREASED SCRATCH = 3 SUCC: ACTIVE VERTEX = V4 SUCC COSTS = 2 INCREASED SUM-COSTS = -2 SCRATCH BEFORE = 2 INCREASED SCRATCH = 3 SUCC: ACTIVE VERTEX = V5 SUCC COSTS = 8 INCREASED SUM-COSTS = 4 SCRATCH BEFORE = 4 INCREASED SCRATCH = 5 SUCC: ACTIVE VERTEX = V6 SUCC COSTS = 4 INCREASED SUM-COSTS = 0 SCRATCH BEFORE = 2 INCREASED SCRATCH = 3 SUCC: ACTIVE VERTEX = V0 SUCC COSTS = 4 SUCC: ACTIVE VERTEX = V5 SUCC COSTS = 5 INCREASED SUM-COSTS = 3 SCRATCH BEFORE = 5 DECREASED SCRATCH = 5 SUCC: ACTIVE VERTEX = V1 SUCC COSTS = -10 INCREASED SUM-COSTS = -12 SCRATCH BEFORE = 4 INCREASED SCRATCH = 5 SUCC: ACTIVE VERTEX = V6 SUCC COSTS = 6 SUCC: ACTIVE VERTEX = V5 SUCC COSTS = 1 INCREASED SUM-COSTS = 1 SCRATCH BEFORE = 6 INCREASED SCRATCH = 7 SUCC: ACTIVE VERTEX = V3 SUCC COSTS = 3 INCREASED SUM-COSTS = -9 SCRATCH BEFORE = 4 INCREASED SCRATCH = 5 SUCC: ACTIVE VERTEX = V2 SUCC COSTS = 2 INCREASED SUM-COSTS = -7 SCRATCH BEFORE = 4 INCREASED SCRATCH = 5 SUCC: ACTIVE VERTEX = V4 SUCC COSTS = 2 INCREASED SUM-COSTS = -7 SCRATCH BEFORE = 4 INCREASED SCRATCH = 5 SUCC: ACTIVE VERTEX = V5 SUCC COSTS = 8 INCREASED SUM-COSTS = -1 SCRATCH BEFORE = 8 INCREASED SCRATCH = 9 SUCC: ACTIVE VERTEX = V6 SUCC COSTS = 4 INCREASED SUM-COSTS = -5 SCRATCH BEFORE = 4 INCREASED SCRATCH = 5 SUCC: ACTIVE VERTEX = V0 SUCC COSTS = 4 INCREASED SUM-COSTS = -3 SCRATCH BEFORE = 2 INCREASED SCRATCH = 3 SUCC: ACTIVE VERTEX = V5 SUCC COSTS = 5 INCREASED SUM-COSTS = -2 SCRATCH BEFORE = 9 DECREASED SCRATCH = 9 SUCC: ACTIVE VERTEX = V1 SUCC COSTS = -10 INCREASED SUM-COSTS = -17 SCRATCH BEFORE = 6 INCREASED SCRATCH = 7 SUCC: ACTIVE VERTEX = V6 SUCC COSTS = 6 SUCC: ACTIVE VERTEX = V5 SUCC COSTS = 1 INCREASED SUM-COSTS = -4 SCRATCH BEFORE = 10 INCREASED SCRATCH = 11 SUCC: ACTIVE VERTEX = V1 SUCC COSTS = 2 SUCC: ACTIVE VERTEX = V3 SUCC COSTS = 1 SUCC: ACTIVE VERTEX = V3 SUCC COSTS = 3 INCREASED SUM-COSTS = -14 SCRATCH BEFORE = 6 INCREASED SCRATCH = 7 SUCC: ACTIVE VERTEX = V2 SUCC COSTS = 2 INCREASED SUM-COSTS = -12 SCRATCH BEFORE = 6 INCREASED SCRATCH = 7 SUCC: ACTIVE VERTEX = V4 SUCC COSTS = 2 INCREASED SUM-COSTS = -12 SCRATCH BEFORE = 6 INCREASED SCRATCH = 7 SUCC: ACTIVE VERTEX = V5 SUCC COSTS = 8 INCREASED SUM-COSTS = -6 SCRATCH BEFORE = 12 INCREASED SCRATCH = 13 SUCC: ACTIVE VERTEX = V6 SUCC COSTS = 4 INCREASED SUM-COSTS = -10 SCRATCH BEFORE = 6 INCREASED SCRATCH = 7 SUCC: ACTIVE VERTEX = V0 SUCC COSTS = 4 INCREASED SUM-COSTS = -8 SCRATCH BEFORE = 4 INCREASED SCRATCH = 5 SUCC: ACTIVE VERTEX = V5 SUCC COSTS = 5 INCREASED SUM-COSTS = -7 SCRATCH BEFORE = 13 DECREASED SCRATCH = 13 SUCC: ACTIVE VERTEX = V1 SUCC COSTS = -10 INCREASED SUM-COSTS = -22 SCRATCH BEFORE = 8 INCREASED SCRATCH = 9 SUCC: ACTIVE VERTEX = V6 SUCC COSTS = 6 SUCC: ACTIVE VERTEX = V5 SUCC COSTS = 1 INCREASED SUM-COSTS = -9 SCRATCH BEFORE = 14 INCREASED SCRATCH = 15 SUCC: ACTIVE VERTEX = V1 SUCC COSTS = 2 SUCC: ACTIVE VERTEX = V3 SUCC COSTS = 1 SUCC: ACTIVE VERTEX = V3 SUCC COSTS = 3 INCREASED SUM-COSTS = -19 SCRATCH BEFORE = 8 INCREASED SCRATCH = 9 ACTUAL SCRATCH BEFORE EXCEPTION = 16 GraphException: Negative cycle detected gerd@goedel:~/WEB-MATERIAL/fh/I-ALGO/I-ALGO-EX/EX7/G0>
6.2.3 Show the efficiency of the implementation related to memory and time
See exercises.
|
Table of some Graph-Algorithms |
|||||
|
PROBLEM |
+/- DIR |
+/- CYCL |
- WEIGHTED |
+ WEIGHTED |
|
|
+ POS.WEIGHTED |
+ NEG.WEIGHTED |
||||
|
Topological Sort |
+ DIR |
- CYCL |
--- |
--- |
--- |
|
Shortest Path |
+ DIR |
- CYCL |
--- |
+++ |
+++ |
// Single-source weighted shortest-path algorithm for acyclic graphs.
void Graph::acyclic( const string & startName ) {
vmap::iterator itr = vertexMap.find( startName );
if( itr == vertexMap.end( ) ){
cerr << "GraphException: startName is not a vertex in this graph" << endl;
return;
}
clearAll( );
Vertex *start = (*itr).second;
list<Vertex *> q;
start->dist = 0;
// Compute the indegrees
for( itr = vertexMap.begin( ); itr != vertexMap.end( ); ++itr )
{
Vertex *v = (*itr).second;
for( int i = 0; i < v->adj.size( ); i++ )
v->adj[ i ].dest->scratch++;
}
// Enqueue vertices of indegree zero
for( itr = vertexMap.begin( ); itr != vertexMap.end( ); ++itr )
{
Vertex *v = (*itr).second;
if( v->scratch == 0 )
q.push_back( v );
}
int iterations;
for( iterations = 0; !q.empty( ); iterations++ )
{
Vertex *v = q.front( );
q.pop_front( );
for( int i = 0; i < v->adj.size( ); i++ )
{
Edge e = v->adj[ i ];
Vertex *w = e.dest;
double cvw = e.cost;
if( --w->scratch == 0 )
q.push_back( w );
if( v->dist == INT_MAX )
continue;
if( w->dist > v->dist + cvw )
{
w->dist = v->dist + cvw;
w->prev = v;
}
}
}
if( iterations != vertexMap.size( ) ){
cerr << "GraphException: Graph has a cycle!" << endl;
return;
}
}
6.3.1 Informal description of the problem
Given a directed weighted graph. Select an arbitrary vertex for start. Search for the shortest possible path.
Remark: The algorithm should search for all possible paths, but show then only the shortest one with the goal given by the user.
6.3.2 Formal description of the solution (using pseudo-code, structured programming, C++-Code)
Considering correctness and completeness
The idea is to apply a simple topological-sort algorithm first and then, if this algorithm doesn't fail, one knows that the graph is acyclic. Then one can apply a simplified shortest path algorithm which works only forward.
gerd@goedel:~/WEB-MATERIAL/fh/I-ALGO/I-ALGO-EX/EX7/G0> ./g0 g1.txt Reading file... TEST: A B 5 TEST: A C 20 TEST: B C 15 TEST: B E 5 TEST: C D 35 TEST: C E 25 TEST: D A 3 TEST: E D 7 TEST: E F 7 TEST: F B 8 File read CONTINUE (y/n) ?: y Enter start node: A Enter destination node: F Enter algorithm (u, n, a): a GraphException: Graph has a cycle! F is unreachable CONTINUE (y/n) ?: y Enter start node: A Enter destination node: D Enter algorithm (u, n, a): a GraphException: Graph has a cycle! D is unreachable CONTINUE (y/n) ?: n gerd@goedel:~/WEB-MATERIAL/fh/I-ALGO/I-ALGO-EX/EX7/G0>
gerd@goedel:~/WEB-MATERIAL/fh/I-ALGO/I-ALGO-EX/EX7/G0> ./g0 g2.txt Reading file... TEST: A B 5 TEST: A C 20 TEST: B C 15 TEST: B E 5 TEST: C D 35 TEST: C E -25 TEST: D A 3 TEST: E D 7 TEST: E F 7 TEST: F B 8 File read CONTINUE (y/n) ?: y Enter start node: A Enter destination node: F Enter algorithm (u, n, a): a GraphException: Graph has a cycle! F is unreachable CONTINUE (y/n) ?: n gerd@goedel:~/WEB-MATERIAL/fh/I-ALGO/I-ALGO-EX/EX7/G0>
gerd@goedel:~/WEB-MATERIAL/fh/I-ALGO/I-ALGO-EX/EX7/G0> ./g0 g3.txt Reading file... TEST: A B 5 TEST: A C 20 TEST: B C 15 TEST: B E 5 TEST: C D 35 TEST: C E -25 TEST: A D 3 TEST: E D 7 TEST: F E 7 TEST: B F 8 File read CONTINUE (y/n) ?: y Enter start node: A Enter destination node: F Enter algorithm (u, n, a): a (Cost is: 13) A to B to F CONTINUE (y/n) ?: y Enter start node: A Enter destination node: E Enter algorithm (u, n, a): a (Cost is: -5) A to C to E CONTINUE (y/n) ?: y Enter start node: A Enter destination node: D Enter algorithm (u, n, a): a (Cost is: 2) A to C to E to D CONTINUE (y/n) ?: n gerd@goedel:~/WEB-MATERIAL/fh/I-ALGO/I-ALGO-EX/EX7/G0>
6.3.3 Show the efficiency of the implementation related to memory and time
See exercises.
Compute the time-complexity of the above mentioned algorithms.
Negative-weighted algorithm:
Find an example-graph with 4 vertices having a negative cost cycle.
Apply the algorithm and examine why the algorithm is running into such a loop.
Analyze how to overcome such a loop.
Prove that the algorithm of Weiss is correct.
Weighted acyclic graph algorithm:
Examine this algorithm how it recognizes a cycle?
Explain, why this algorithm has no problems with negative costs too.
Prove the correctness of this algorithm.