
|
|
|
I-ALGO SS03 - ALGORITHMS AND DATASTRUCTURES - Lecture with Exercices
|
Within the realm of computer applications are random numbers playing a very important role. There are many kinds of applications which are unthinkable without random numbers, e.g.:
Simulation: for the simulation of all kinds of environment and environmental events you need some 'randomness'.
Sampling: to get the right 'size' of data sets as well as a rich enough 'variation' you need random numbers helping you to select possible data.
Numerical Analysis: there are mathematical problems which only could be solved using random numbers; especially also algorithms which are theoretically untractable but with the usage of random numbers they can be managed in a way that for most cases an application is becoming possible.
Computer Programming: testing the correctness and effectiveness of algorithms is done by random input sets.
Decision making: there are many situations in which the application of fixed rules is either 'slow' or is even leading to unsolvable cases; randomness is breaking the barrier.
Recreation: most games rely on 'random events'; the socalled 'Monte Carlo Method' is a kind of generalization which is used in many apllications, pratically, technically and scientific.
Thus it is very useful to know, what random numbers are, how one can generate such numbers and how one can test the 'quality' of generated random numbers.
For the following I have mainly used [BOSCH 1979], [CLAUSS/EBNER 1983], [WHITNEY 1984], [FRÜHWIRT/REGLER 1983], and the chapter 3 of [KNUTH 1981]. Other sources are cited below. For all the numerical demonstrations and the related graphical output I am using the opensource software package 'scilab' from INRIA.
There exist no random numbers but only random processes producing events which are 'random'.
A random process can be characterized as a process with no memory of past events producing new events and you cannot predict with certainty the next event.
Examples of 'natural' random processes:
Throwing a dice.
Flipping a coin.
Observing the last digits of the phonenumbers in a phonebook.
Observing th last digit of the licence plate numbers of passing cars.
Samples of suggested random events can be characterized by several empirical indicators. We select here the following three (for others see the cited literature under the subject of 'descriptive statistics'):
Modeling a random process with deterministic algorithms on finite machines.
The finite machine gives you a maximal number Imax = 2e-1 (with e as number of bits in the computerword)
The deterministic algorithms urges you to define a deterministic process which approximates 'randomness'.
Generator for a uniform distribution, others --like e.g. gaussian-- can be gained out of uniform distributions.
mod(I,m) = I - int(I,m)*m
Linear Congruential Generator (LCG): Ii+1 = mod(a*Ii+c,m)
also written as: Ii+1 = a*Ii+c % m
Producing integers in the range [0,m-1]; period m, deterministic
Normalizing for the range [0,(m-1)/m] with xi+1 = float(Ii+1)/float(m)
period := Start from position 1 (:= x1) and find the next value xn = x1, then n-1 is the period
'Rules of Thumb' (derived from theorems):
m and c must not have a factor in common
a > sqrt(m)
longest possible periods with m is a prime number and m <= Imax
a*m+c < Imax
Use a generator out to one-half of it's period
Use 'shuffling' by at least 2 LCGs in parallel (see Whitney for a commented example and some code)
For the 'construction' of a good set of parameters it is useful to work with primes.
Def: A p in Nat* is a prime if p > 1 and p is divisible by 1 or by itself.
Theorem: For all n in Nat* with n > 1 it holds, that n can be represented as a product of primes: n = p1a_1 * p2a_2 * ... * pka_k with a_i in Nat+ u {0} and p_i primal factors of n
Example 1:
a=17; a > sqrt(m) and a has no common divisor with m because m is prime and a is prime
c=17; c has no common divisor with m because m is prime and c is prime
m=257; m is prime and m < Imax
a*m+c < Imax
i0 = 1
The LCG with In+1 = Mod(a,In+c,m) (Mod generates in case of '-' a zero!) has the following output:
DATA 1:
34. 81. 109. 71. 196. 8. 153. 48. 62. 43. 234. 140. 84. 160.
167. 29. 253. 206. 178. 216. 91. 22. 134. 239. 225. 244. 53.
147. 203. 127. 120. 1. 34. 81. 109. 71. 196. 8. 153. 48.
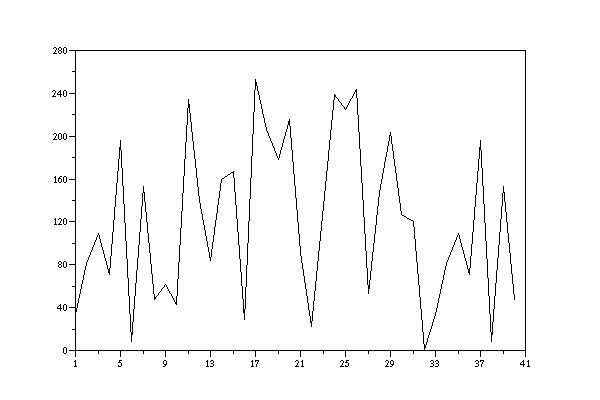
LCG-output with a=17, c=17, m=257, i_0=1
One can see, that the first number is repeated at position 33, that means that we have a period of length 32.
Example 2:
a=17; a > sqrt(m) and a has no common divisor with m because m is prime and a is prime
c=17; c has no common divisor with m because m is prime and c is prime
m=65536; 17 is not a divisor of m & m < Imax
a*m+c < Imax
i0 = 1
The LCG with these parameters has the following output:
DATA 2: 34. 595. 10132. 41189. 44870. 41911. 57144. 53961. 65386. 63003. 22492. 54701. 12430. 14719. 53632. 59793. 33458. 44515. 35876. 20085. 13782. 37703. 51144. 17497. 35322. 10667. 50284. 2877. 48926. 45327. 49680. 58145. 5442. 26995. 180. 3077. 52326. 37591. 49240. 50665. 9354. 27963. 16636. 20685. 23982. 14495. 49824. 60593. 47058. 13571. 34116. 55701. 29430. 41575. 51432. 22393. 53018. 49355. 52620. 42589. 3134. 53295. 54064. 1601. 27234. 4243. 6612. 46885. 10630. 49655. 57720. 63753. 35242. 9307. 27164. 3053. 51918. 30655. 62400. 12241. 11506. 64547. 48740. 42165. 61462. 61831. 2568. 43673. 21562. 38891. 5804. 33149. 39262. 12111. 9296. 26977. 65410. 63411. 29428. 41541.
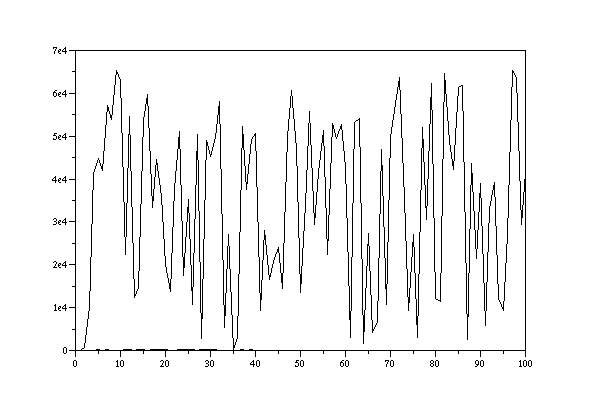
LCG-output with a=17, c=17, m=65536, i_0=1
One can see, that there is no repetition within the first 100 numbers and a simple detection algorithms shows, that there is no repetition before 65536.
One can 'map' the output of the LCG into the range of [0,1] by setting In+1 = In+1/m, which transforms the sequence above into:
DATA 3: 0.000518798828 0.00907897949 0.154602051 0.628494263 0.684661865 0.639511108 0.871948242 0.823379517 0.997711182 0.961349487 0.343200684 0.834671021 0.189666748 0.224594116 0.818359375 0.912368774 0.510528564 0.679244995 0.547424316 0.306472778 0.210296631 0.575302124 0.780395508 0.266983032 0.538970947 0.162765503 0.767272949 0.0438995361 0.746551514 0.691635132 0.758056641 0.88722229 0.0830383301 0.411911011 0.00274658203 0.0469512939 0.798431396 0.57359314 0.751342773 0.773086548 0.142730713 0.426681519 0.253845215 0.315628052 0.365936279 0.221176147 0.760253906 0.924575806 0.718048096 0.207077026 0.520568848 0.84992981 0.449066162 0.634384155 0.784790039 0.341690063 0.808990479 0.753097534 0.80291748 0.649856567 0.0478210449 0.813217163 0.824951172 0.0244293213 0.415557861 0.064743042 0.100891113 0.715408325 0.162200928 0.757675171 0.880737305 0.972793579 0.537750244 0.14201355 0.414489746 0.046585083 0.792205811 0.467758179 0.952148438 0.186782837 0.175567627 0.984909058 0.743713379 0.643386841 0.937835693 0.943466187 0.0391845703 0.666397095 0.32901001 0.593429565 0.0885620117 0.505813599 0.599090576 0.184799194 0.141845703 0.411636353 0.998077393 0.967575073 0.449035645 0.633865356
If one accepts some 'bluriness' in the numbers one can transform the original output In+1 in a special range [1,upper] with the formula xn+1 = round( (In+1 * upper - In+1 )/m )+1.
DATA 4: 1. 1. 2. 4. 4. 4. 5. 5. 6. 6. 3. 5. 2. 2. 5. 6. 4. 4. 4. 3. 2. 4. 5. 2. 4. 2. 5. 1. 5. 4. 5. 5. 1. 3. 1. 1. 5. 4. 5. 5. 2. 3. 2. 3. 3. 2. 5. 6. 5. 2. 4. 5. 3. 4. 5. 3. 5. 5. 5. 4. 1. 5. 5. 1. 3. 1. 2. 5. 2. 5. 5. 6. 4. 2. 3. 1. 5. 3. 6. 2. 2. 6. 5. 4. 6. 6. 1. 4. 3. 4. 1. 4. 4. 2. 2. 3. 6. 6. 3. 4.
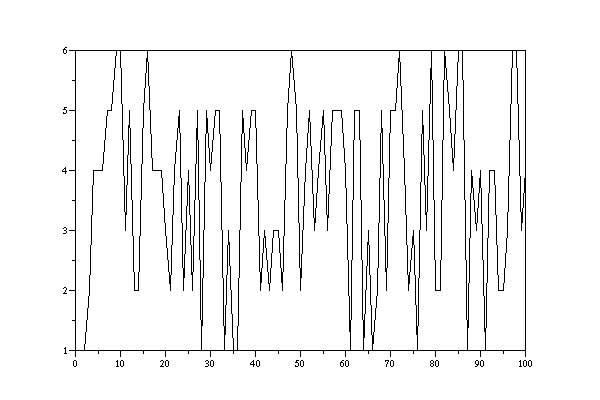
LCG-output with a=17, c=17, m=65536, i_0=1, transformed into [1,6]
Here a simple test-programm of the LCG in C++:
//--------------------------
//
// lcg1.cpp
//
// author: gerd d-h
// first: june-26, 2003
//
// idea: demonstrator of a simple LCG
// (LCG := Linear Congruential Generator)
// si = (a * io+c) % m
//
// Compilation: g++ -o lcg1 lcg1.cpp
// Usage: lcg1
//
//-------------------------------------------------
#include <iostream>
#include <cstdlib> //for EXIT_FAILURE
int main(){
unsigned int a,c; //Coefficients of LCG-formula
int si,io;
unsigned int m;
unsigned int j,n; //Number of runs
char yes;
float upper = 1.0;
int xn;
double fn;
cout << "HOW MANY NUMBERS DO YOU WANT ? (Stop with '0')";
cin >> n;
cout <<"PLEASE ENTER COEFFICIENTS: ";
cout << endl <<"a = ";
cin >> a;
cout << endl <<"c = ";
cin >> c;
cout << endl <<"m = ";
cin >> m;
if ( m == 0) {
cerr << "ERROR: DIVISOR HAS TO BE NOT ZERO !";
return EXIT_FAILURE;
}
cout << endl <<"PLEASE ENTER SEED: ";
cout << endl <<"io = ";
cin >> io;
cout << "DO YOU WANT AN INTERVALL (y/n) ?" ;
cin >> yes;
if (yes == 'y') {
cout << "[0,1] ---------> r " << endl;
cout << "[1,upper] -----> u " << endl;
cin >> yes;
switch(yes){
case 'r': {
upper =2.0;
break;
}
case 'u': {
cout << "PLEASE ENTER UPPER : ";
cin >> upper;
break;
}
default: {
cerr << "ERROR: WRONG INTERVALL !!!";
return EXIT_FAILURE;
}
}
}//end yes intervall
j=0;
while(j < n){
si = (a * io+c) % m;
if (upper > 1) {
switch(yes){
case 'r': {
fn = si * 1.0 /m *1.0;
cout << j << " = " << fn << endl;
break;
}
case 'u': {
xn=((si * upper-si)/m+1)+1;
cout << j << " = " << xn << endl;
break;
}
default: {
cerr << "ERROR: WRONG INTERVALL !!!";
return EXIT_FAILURE;
}
}
}//End of if upper
else {
cout << j << " = " << si << endl;}
io = si;
j++;
}
}
This produces the following outputs:
gerd@goedel:~/WEB-MATERIAL/fh/I-ALGO/I-ALGO-EX/EX4> ./lcg1 HOW MANY NUMBERS DO YOU WANT ? (Stop with '0')20 PLEASE ENTER COEFFICIENTS: a = 17 c = 17 m = 65536 PLEASE ENTER SEED: io = 1 DO YOU WANT AN INTERVALL (y/n) ?n 0 = 34 1 = 595 2 = 10132 3 = 41189 4 = 44870 5 = 41911 6 = 57144 7 = 53961 8 = 65386 9 = 63003 10 = 22492 11 = 54701 12 = 12430 13 = 14719 14 = 53632 15 = 59793 16 = 33458 17 = 44515 18 = 35876 19 = 20085 gerd@goedel:~/WEB-MATERIAL/fh/I-ALGO/I-ALGO-EX/EX4> ./lcg1 HOW MANY NUMBERS DO YOU WANT ? (Stop with '0')20 PLEASE ENTER COEFFICIENTS: a = 17 c = 17 m = 65536 PLEASE ENTER SEED: io = 1 DO YOU WANT AN INTERVALL (y/n) ?y [0,1] ---------> r [1,upper] -----> u r 0 = 0.000518799 1 = 0.00907898 2 = 0.154602 3 = 0.628494 4 = 0.684662 5 = 0.639511 6 = 0.871948 7 = 0.82338 8 = 0.997711 9 = 0.961349 10 = 0.343201 11 = 0.834671 12 = 0.189667 13 = 0.224594 14 = 0.818359 15 = 0.912369 16 = 0.510529 17 = 0.679245 18 = 0.547424 19 = 0.306473 gerd@goedel:~/WEB-MATERIAL/fh/I-ALGO/I-ALGO-EX/EX4> gerd@goedel:~/WEB-MATERIAL/fh/I-ALGO/I-ALGO-EX/EX4> ./lcg1 HOW MANY NUMBERS DO YOU WANT ? (Stop with '0')20 PLEASE ENTER COEFFICIENTS: a = 17 c = 17 m = 65536 PLEASE ENTER SEED: io = 1 DO YOU WANT AN INTERVALL (y/n) ?y [0,1] ---------> r [1,upper] -----> u u PLEASE ENTER UPPER : 6 0 = 2 1 = 2 2 = 2 3 = 5 4 = 5 5 = 5 6 = 6 7 = 6 8 = 6 9 = 6 10 = 3 11 = 6 12 = 2 13 = 3 14 = 6 15 = 6 16 = 4 17 = 5 18 = 4 19 = 3 gerd@goedel:~/WEB-MATERIAL/fh/I-ALGO/I-ALGO-EX/EX4>
To detect in such a transformed series directly a period only by loocking for the repetition of one of the numbers in the series is not any more possible, because those repetitions of the same numbers occur on an irregular ('random') basis. Below we will investigate some of the many possible 'tests' intended to check the 'quality' of the 'randomness' of such series.
The next example is taken from the book [WEISS 2000:369ff]. Weiss is representing his code in C++, we are using here again scilab. Generally he is using a LCG without the increment-parameter 'c', i.e. c=0. Then he is taking the maximal available number for m = 2^31-1 (which is a prime number!). Thus any other combinations of smaller primes has no factor in common with m. He presents then for the parameter a the value a=48271 (without explanation) telling that this value for a gives a full-period LCG. But because a division like modulo(In/m) can yield an overflow on 32-bit machines he proposes --as other authors do as well-- to split the number m into the quotient q and the remainder r as follows:
Then he gives the following algorithm (here in the scilab-version):
t=a*modulo(i,q) - r*(i/q) if t >= 0 then, i = t else i = t + m end [i]=return(i)
Applying this algorithm with these values we are getting the first 30 numbers (normalized to m) as follows:
0.0309277071 0.845361465 0.77319268 0.134036605 0.329816977 0.350915117 0.245424416 0.772877922 0.135610393 0.321948036 0.390259822 0.0487008908 0.756495546 0.217522273 0.912388638 0.438056815 0.809715929 0.951420359 0.242898212 0.785508942 0.0724552917 0.637723542 0.811382294 0.943088534 0.284557333 0.577213334 0.113933331 0.430333346 0.848333271 0.75833365
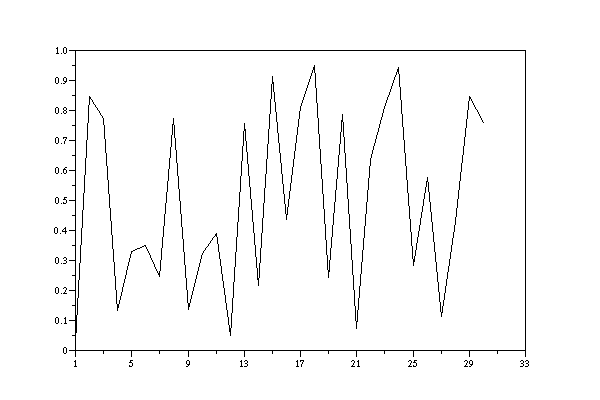
LCG-output with a=48271, c=0, m=2^31-1 decomposed in quotient q and remainder r, i_0=1, transformed into [0,1]
As one can see from the considerations above is it always necessary to test the output of a random number generator. It is recommended to use different tests because no single test can give a complete judgement about the quality of the number generator. In the following we will give two tests explicitly, others should looked at in the cited literature (cf. [KNUTH 1981:Vol2]).
The first question to answer ist: what should we test? We have as one parameter the output of the LCG, but what is the other parameter to which we want to compare the LCG output?
What we need is an ideal measure of randomness, i.e. the random output of a 'true' random process. Here we have two possibilities: (i) either we have empirical samples of processes which we are calling 'truely' random processes or we have abstract (ideal) models of random processes which we can use as some 'norm' to compare these idealized models with their output against our processes in question.
Possbility (i) doesn't really help because to classify something as an utput of a 'true' random process presupposes already some concept of randomness. Thus we are forced to look to possibility (ii).
To set up formal (idealized) models of random processes has been done in the science of mathematics since the 19th century (cf. an overview about the history in [SCHNEIDER 1988]). Meanwhile several formal models are available (see below). Because we have here only one lecture we can not deal with the theory of statistics and probability. But we will consider two cases of formal models which can be used to evaluate the quality of the output of our random generator.
The basic idea behind all these formal models of randomness is using the fact that single events can tell you nothing, but samples of events, especially if they become larger and larger, are showing in many cases certain 'shapes of a distribution'. The basic distinction is between 'uniform distributions' and 'nonuniform distributions'. Examples of nonuniform distributions' are very numerous. Some of the most important ones are the gaussian (normal) distribution, the poisson distribution, the negative exponential distribution, the binomial, the chi2 (chi-square), the t and the exponential distribution (see e.g. [FRÜHWIRT/REGLER 1983] or [BOSCH 1979] for more explanations.). Beause one can convert a normal distribution into another distribution it is a good starting point for a random number generator to produce a uniform output, which can then be converted into other needed distributions.
In a uniform distribution we have the theoretical assumption that any of the possible values of the random process under investigation can be classified according a finite set of k bins, and the values of all bins are evenly likely to occur. There will be also repetitions of values, but these repetitions are 'irregular', i.e. you can not predict the next repetition. Thus if we would simulate an ideal dice with the possible values {1,...,6} and we would map these values 1-to-1 into 6 bins (or categories), then we would have with n=18 events 18 possible events which can belong to one of the assumed 6 categories. Assuming --according to a uniform distribution-- that every value has 'the same chance' we should in an ideal case assume that we have a relationship of 18:6, that means we would have to assume 3:1 for each category. Let us deal with this case a bit more (see below).
Taking an LCG with the output shown in the data set DATA 4, we can compute an empirical mean with x-bar= 3.64. Classifying the values according the categories 1...6 we find the frequencies:
CAT FREQ --------- 1 12. 2 17. 3 14. 4 20. 5 26. 6 11. -------- n = 100
As empirical variance si2 and empirical standard-deviation si we get:
x-bar = 3.65 si2 =2.4953535 si = 1.5796688
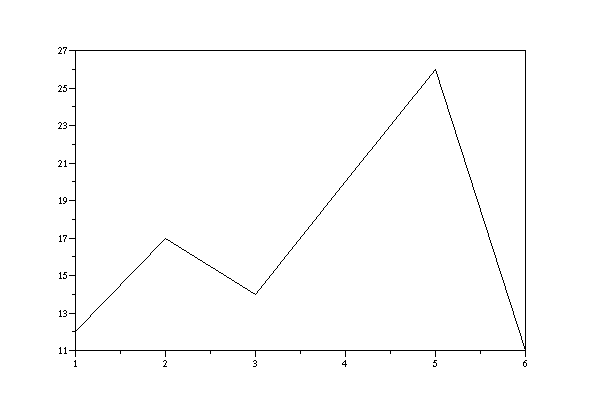
LCG-output with a=17, c=17, m=65536, i_0=1, transformed into [1,6], n=100, x-bar = 3.65, si2 =2.4953535, si = 1.5796688
These are the observed empirical values of our experiment with the random generator. The theoretical case can be described vary easily. We have 100:6 = 16.666667 for the individual frequency, thus we get: my = 3.5. For the theoretical standard-deviation sigma we get sigma = 1.72 and for the theoretical variance we are getting sigma2 = 2.95.
my = 3.5 sigma2 = 2.95 sigma = 1.72
Another way to cope with the output of our LCG-generator is to apply the chi-square test (see for details the cited literature or the following online tutorials: Chi-square test tutorial by Prof. Jeff Connor-Linton from the Department of Linguistics at Georgetown University or the chi-square test by David M.LANE).
chi square is a nonparametric test. It does not require the sample data to be more or less normally distributed (as parametric tests like t-tests do), although it relies on the assumption that the variable is normally distributed in the population from which the sample is drawn.
The test compares the observed values of a sample foi --in our case the output of an LCG-- with theoretically expected values fei --taken from some 'ideal' case--.
As you can see from the formula below, it subtracts the expected values from the observed values, squares the differences to eliminate the possible negative signs, and does a weighting with the expected values.
chi2(X,k) = SUM(i=1,k)(foi - fei)2/fei
k := Number of bins (or categories)
X := random Variable with k independent bins (or categories)
foi := observed frequencies
fei := theoretically expected frequencies
If the observed and the expected values would be identical, then the chi2-value would be 0. If the observed values would be different from the expected values, then we would have k-times some proportion d/fei, which could become arbitrarily large. Thus the question is, which kind of value is 'good enough' to be taken as index of agreement between empirical sample and theoretical case? Let us look to an example.
To apply the chi2-test one has to accept some requirements:
Let us apply this test to our example with the data set DATA 4 from above.
The oberved frequencies foi are those which result from the output of the LCG. The theoretically expected frequencies fei are computed from the ideal uniform distribution, i.e. we have n=100 and k=6 categories. Thus every category has theoretically the 'probability' of 100:6 = 16.66667. If we are using these values, we get a chi2-value of 9.56.
The question is, what does this number '9.56' tell us? Is it 'good' or 'bad'?
To answer this question one has to convert it into the formula: how probable is it to have a chi2-value of '9.95', i.e. in how many cases will chi2 be greater than this value?
To answer this version one has to take into account two more parameters: the level of significance a and the degree of freedom df.
The level of significance tells us, in how many cases measured in percentage (%) the value will be surpassed. A
value of a=0.05 would state that the probability to get a certain value in the table is equal or greater to 5%.The
degree of freedom takes into account the number of independent categories (and parameters) used in the computation. In
our case we have K=6 categories. The formula states then df=k-1 = 5.Thus with a level of significance of a=0.05
and a degree of freedom with df=5 --written: chi2(a;f)-- we would find in the table below the value: 11.0705.
Thus we have
chi2= 9.95 < chi2(0.05; 5) = 11.0705.
This tells us, that according to the chi2-test our empirical values are in 95% of all cases as the values 'would be
expected'.
Table for the Chi Square Distribution (see also: chi-square table and computing programs).
Significance Level
df 0.10 0.05 0.025 0.01 0.005
1 2.7055 3.8415 5.0239 6.6349 7.8794
2 4.6052 5.9915 7.3778 9.2104 10.5965
3 6.2514 7.8147 9.3484 11.3449 12.8381
4 7.7794 9.4877 11.1433 13.2767 14.8602
5 9.2363 11.0705 12.8325 15.0863 16.7496
6 10.6446 12.5916 14.4494 16.8119 18.5475
7 12.017 14.0671 16.0128 18.4753 20.2777
8 13.3616 15.5073 17.5345 20.0902 21.9549
9 14.6837 16.919 19.0228 21.666 23.5893
10 15.9872 18.307 20.4832 23.2093 25.1881
11 17.275 19.6752 21.92 24.725 26.7569
12 18.5493 21.0261 23.3367 26.217 28.2997
13 19.8119 22.362 24.7356 27.6882 29.8193
14 21.0641 23.6848 26.1189 29.1412 31.3194
15 22.3071 24.9958 27.4884 30.578 32.8015
16 23.5418 26.2962 28.8453 31.9999 34.2671
17 24.769 27.5871 30.191 33.4087 35.7184
18 25.9894 28.8693 31.5264 34.8052 37.1564
19 27.2036 30.1435 32.8523 36.1908 38.5821
20 28.412 31.4104 34.1696 37.5663 39.9969
21 29.6151 32.6706 35.4789 38.9322 41.4009
22 30.8133 33.9245 36.7807 40.2894 42.7957
23 32.0069 35.1725 38.0756 41.6383 44.1814
24 33.1962 36.415 39.3641 42.9798 45.5584
25 34.3816 37.6525 40.6465 44.314 46.928
26 35.5632 38.8851 41.9231 45.6416 48.2898
27 36.7412 40.1133 43.1945 46.9628 49.645
28 37.9159 41.3372 44.4608 48.2782 50.9936
29 39.0875 42.5569 45.7223 49.5878 52.3355
30 40.256 43.773 46.9792 50.8922 53.6719
31 41.4217 44.9853 48.2319 52.1914 55.0025
32 42.5847 46.1942 49.4804 53.4857 56.328
33 43.7452 47.3999 50.7251 54.7754 57.6483
34 44.9032 48.6024 51.966 56.0609 58.9637
35 46.0588 49.8018 53.2033 57.342 60.2746
36 47.2122 50.9985 54.4373 58.6192 61.5811
37 48.3634 52.1923 55.668 59.8926 62.8832
38 49.5126 53.3835 56.8955 61.162 64.1812
39 50.6598 54.5722 58.1201 62.4281 65.4753
40 51.805 55.7585 59.3417 63.6908 66.766
41 52.9485 56.9424 60.5606 64.95 68.0526
42 54.0902 58.124 61.7767 66.2063 69.336
43 55.2302 59.3035 62.9903 67.4593 70.6157
44 56.3685 60.4809 64.2014 68.7096 71.8923
45 57.5053 61.6562 65.4101 69.9569 73.166
46 58.6405 62.8296 66.6165 71.2015 74.4367
47 59.7743 64.0011 67.8206 72.4432 75.7039
48 60.9066 65.1708 69.0226 73.6826 76.9689
49 62.0375 66.3387 70.2224 74.9194 78.2306
50 63.1671 67.5048 71.4202 76.1538 79.4898
51 64.2954 68.6693 72.616 77.386 80.7465
52 65.4224 69.8322 73.8099 78.6156 82.0006
53 66.5482 70.9934 75.0019 79.8434 83.2525
54 67.6728 72.1532 76.1921 81.0688 84.5018
55 68.7962 73.3115 77.3804 82.292 85.7491
56 69.9185 74.4683 78.5671 83.5136 86.994
57 71.0397 75.6237 79.7522 84.7327 88.2366
58 72.1598 76.7778 80.9356 85.9501 89.477
59 73.2789 77.9305 82.1174 87.1658 90.7153
60 74.397 79.082 83.2977 88.3794 91.9518
61 75.5141 80.2321 84.4764 89.5912 93.1862
62 76.6302 81.381 85.6537 90.8015 94.4185
63 77.7454 82.5287 86.8296 92.0099 95.6492
64 78.8597 83.6752 88.004 93.2167 96.8779
65 79.973 84.8206 89.1772 94.422 98.1049
66 81.0855 85.9649 90.3488 95.6256 99.3303
67 82.1971 87.108 91.5193 96.8277 100.5538
68 83.3079 88.2502 92.6885 98.0283 101.7757
69 84.4179 89.3912 93.8565 99.2274 102.9961
70 85.527 90.5313 95.0231 100.4251 104.2148
71 86.6354 91.6703 96.1887 101.6214 105.4323
72 87.7431 92.8083 97.353 102.8163 106.6473
73 88.8499 93.9453 98.5162 104.0098 107.8619
74 89.9561 95.0815 99.6784 105.2019 109.0742
75 91.0615 96.2167 100.8393 106.3929 110.2854
76 92.1662 97.351 101.9992 107.5824 111.4954
77 93.2702 98.4844 103.1581 108.7709 112.7037
78 94.3735 99.617 104.3159 109.9582 113.9107
79 95.4762 100.7486 105.4727 111.144 115.1163
80 96.5782 101.8795 106.6285 112.3288 116.3209
81 97.6796 103.0095 107.7834 113.5123 117.524
82 98.7803 104.1387 108.9373 114.6948 118.7261
83 99.8805 105.2672 110.0902 115.8762 119.927
84 100.98 106.3949 111.2422 117.0566 121.1262
85 102.0789 107.5217 112.3933 118.2356 122.3244
86 103.1773 108.6479 113.5436 119.4137 123.5218
87 104.275 109.7733 114.6929 120.5909 124.7176
88 105.3723 110.898 115.8415 121.7672 125.9123
89 106.4689 112.022 116.989 122.9422 127.106
90 107.565 113.1452 118.1359 124.1162 128.2987
91 108.6606 114.2679 119.282 125.2893 129.4902
92 109.7556 115.3898 120.427 126.4616 130.6812
93 110.8501 116.511 121.5714 127.633 131.8705
94 111.9442 117.6317 122.7152 128.8032 133.0589
95 113.0377 118.7516 123.858 129.9725 134.2466
96 114.1307 119.8709 125.0001 131.1411 135.4327
97 115.2232 120.9897 126.1414 132.3089 136.6188
98 116.3153 122.1077 127.2821 133.4756 137.803
99 117.4069 123.2252 128.4219 134.6415 138.9869
100 118.498 124.3421 129.5613 135.8069 140.1697
for more detailed discussions see e.g. [FRÜHBERG 1983:218ff].
If we increase the number from n=100 to n=1000 then we see, that the chi2-Values are getting worse.
x-bar = 3.529 s2 = 2.2033624 s = 1.4843727 chi2 = 91.266175
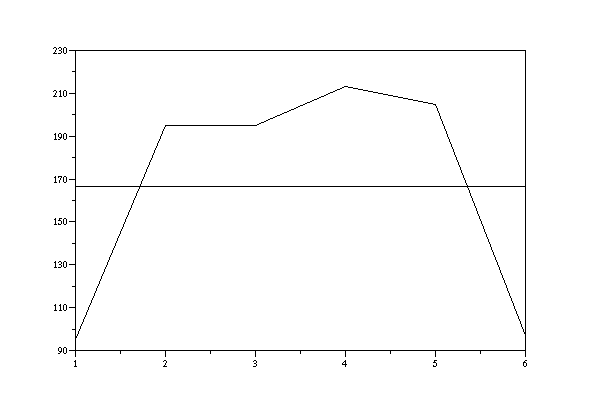
LCG-output with a=17, c=17, m=65536, i_0=1, transformed into [1,6], n=1000, x-bar = 3.529, s2 = 2.2033624, s = 1.4843727 ,chi2 = 91.26617
As one can see from these first considerations is the topic of testing the quality of a random number generator quite fascinating, but by no means trivial. It is beyond these two lectures to give a comprehensive account of all the theory and the necessary concrete examples. For interested readers it is recommended to read the paragraph 'Empirical Tests' by [KNUTH 1981:59ff] where he describes several additional tests especially for testing of random number generators:
Equidistribution
Serial
Poker (Partition)
Coupon Collector
Permutation
Runs
Maximum-of-t
Collision
Serial correlation
Subsequences
Amplitude Spectrum from Fourier Transform (from [WHITNEY 1984])
Do a course in theoretical statistics.... with at least the topics:
Boolean Algebra
Kolmogorov-Axioms
Probabilities in combinatorial spaces
Theoretical distributions (gaussian, binomial, poisson, exponential,...) with density functions
For a more detailed explanation see e.g. [FRÜHWIRTh/REGLER 1983], [CLAUSS/EBNER 1983] and [BOSCH 1979].
See the literature [FRÜHWIRT/REGLER 1983:101ff], how one can transform a uniform distribution into another distribution and the examples in [WEISS 2000:371ff].
Can you give some arguments why it is useful to have some random generator at hand?
What are the characteristic properties of the process which generates 'random' events?
Which parameters of descriptive statistics you know? Give short explanations, what they describe; how are the formulas?
The most widely used method to built random generators ist the linear congruential method providing the so-called Linear Congruential Generator (LCG). Give the formula and explain for what the individual parameters are good for.
There are some 'rules of thumb' (backed up by mathematical theorems) recommending the sizes of the parameters. What are these rules? Can you develop some proposals with these rules?
The output of the LCG used so far consists of positive integers in the range [0,m]. How can you transform the output in other ranges like [0,1] (with floats) or [0,n] (integers with n < m)?
As the example of WEISS shows can an LCG with the biggest possible integer 2e-1 run in trouble on account of overflow during division (This happens if your m is bigger than 1/2 of the sqrt(Imax). To avoid this one can split the parameter m into its quotient q and its remainder r. How does this work? Built an example.
An ideal output of a random number would have the property, that every value is equally probable than any other value. There are many different ways to test this. One simple test: Compute the length of the period of your generator output. Be beware that there can be irregular repetitions which does not tell anything about the real period.
Another simple test is to count the number of odd or even sums of neighbours; odd and even sums should also be evenly distributed
If you can theoretically determine the parameters mean, variance and standard deviation for a certain problem, then can you use these theoretical values as 'point of reference' to measure your empirical output. Give an example how you would do this.
If you have empirical values and theoretical values regarding the frequency of the selected categories, how would you apply the ch2-test onto these data?