
|
|
I-ALGO SS03 - ALGORITHMS AND DATASTRUCTURES - Lecture with Exercices
|
In this lecture we will present the concept of Recursion.
In an informal way it is often said that a recursive function is a function which makes directly or indirectly a call to itself, like in the following simple example seqsum(), where the function seqsum() computes the sum of an initial sequence of the natural numbers, i.e.
seqsum(n) = SUM(i=1,n) i
seqsum(4) = 1 + 2 + 3 + 4 = 10
//---------------------------
//
// seqsum.cpp
//
// example of simple recursion
// computes the sum of a sequence
//
// compile: g++ -o seqsum seqsum.cpp
// usage: seqsum
//
//--------------------------------------
#include <iostream>
using namespace std;
int main( void )
{
extern int seqsum(int);
int n;
cout << "Enter maximal element for summation: " << endl;
cin >> n;
cout << "Result = " << seqsum(n) << endl;
return 0;
}
int seqsum(int n){
if (n == 1) return 1;
else return seqsum(n-1)+n;
}
gerd@turing:~/public_html/I-ALGO/I-ALGO-EX/EX2> seqsum Enter maximal element for summation: 4 Result = 10
In this function seqsum() calls itself but with a different argument. What looks at a first glance a bit like 'magic' reveals itself as a simple and straightforward mechanism.
Behind the 'surface' of the programming language expressions will the compiler translate this code in a machine
readable code and when the automaton is processing functions it will use a stack to store the called functions
before their evaluations.
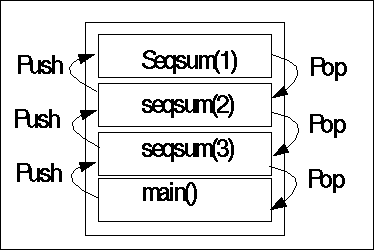
Function Stack
But this informal characterization of recursive functions as functions which call themselves is too simple as to give a full account of what recursive functions are. A more theoretical explanation follows in the next paragraph.
A slightly more general schema for recursive functions is given in the diagram below.
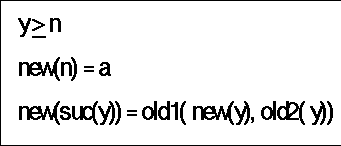
Recursive Function Schema
This schema consists of two parts: in part one (new(n)=a)a function 'new' is declared for a base-case with a fixed value a.In part two (new(suc(y)) ) old1(new(y),old2(y)) we find the more complex schema connecting a new value suc(y) of new with the old value y of new. This is done with the help of some already know functions 'old1' and 'old2'.
Lets look to some examples:
/* Sum */
sm(0,x) = x
sm(suc(y),x) = suc(sm(y,x))
sm(2,3)
suc(sm(1,3))
suc(suc(sm(0,3)))
suc(suc(3))
suc(4)
5
/* Sequential Sum */
ss(1) = 1
ss(suc(y)) = sm(ss(y),suc(y))
ss(3)
sm(ss(2),suc(2)))
sm(sm(ss(1),suc(1)),suc(2)))
sm(sm(1,2),3))
sm(suc(sm(0,2)),3))
sm(suc(2),3))
sm(3,3)
...
6
/* Product */
prod(0,x) = 0
prod(suc(y),x) = sm(prod(y,x),x)
prod(2,2)
sm(prod(1,2),2)
sm(sm(prod(0,2),2),2)
sm(sm(0,2),2)
sm(2,2)
...
4
/* Factorial */
n < 1
fac(n) = 1
fac(suc(y)) = prod(fac(y),suc(y))
fac(3)
prod(fac(2),suc(2))
prod(prod(fac(1),suc(1)),suc(2))
prod(prod(1,2),3)
prod(sm(prod(0,2),2),3)
prod(sm(0,2),3)
prod(2,3)
...
6
/* Fibonacci */
n < 0
fib(n) = 1
fib(suc(y)) = sm(fib(y),fib(vg(y)))
1, 2, 3, 5, 8, 13, ...
position 0: 1
position 1: 2
position 2: 3
...
fib(3)
sm(fib(2),fib(vg(2)))
sm(sm(fib(1),fib(vg(1))),sm(fib(0),fib(vg(0))) )
sm(sm(sm(fib(0),fib(vg(0))),1),sm(1,1) )
sm(sm(sm(1,1),1),sm(1,1) )
sm(sm(2,1),2 )
sm(3,2 )
5
There was an explanation about the Induction principle and why and how this principle can give the theoretical basis for recursive definitions.
With the recursive definition of the fibonacci numbers an example was given, which has been analyzed and which showed that the time capacities needed for such an algorithm can be in the order of O(N2). Thus recursion has to be used with 'care'.