Klausur ALGORITHMEN u. DATENSTRUKTUREN

Dozent: Döben-Henisch


2.Juli 2003, 10:00-12:30h, Raum BCN 121



MATRIKELNUMMER:__________________
NAME: ________________________________________________
PUNKTE INSGESAMT: ______
NOTE: ____

1. Regularien

  1. Teilnehmer an der Klausur müssen sich durch Lichtbildausweis identifizieren.
  2. Es dürfen nur leere Blätter, Schreibgeräte und Taschenrechner benutzt werden. Alle Blätter müssen mit Name und Matr.Nummer gekennzeichnet sein. Blätter ohne Kennzeichen werden nicht berücksichtigt.
  3. Die Klausurzeit beträgt 150 Min. Man darf seinen Platz erst verlassen, wenn der Prüfungsleiter die Klausurarbeit in Empfang genommen hat.
  4. Es gilt folgende Punktetabelle:
    1. >69
    2. 55-69
    3. 40-54
    4. 25-39
    5. <25
  5. Das aktive Abschreiben wie auch das Zulassen von Abschreiben wird als Täuschungsversuch bewertet.

2. Aufgaben


  1. Datenstrukturen
    PKT. MAXIMAL: 9
    PKT. ERREICHT: ______
    Im Rahmen der Vorlesung wurden u.a. folgende Datenstrukturen am Beispiel der Implementierung der C++-Standard-Bibliothek behandelt: Deque, Stack, Queue, Priority Queue, Linked List, und (Multi-)Map. Geben sie eine kurze Beschreibung der wesentlichen Eigenschaften dieser Datenstrukturen und wodurch sie sich voneinander unterscheiden.
  2. Zeitbedarf von Algorithmen
    PKT. MAXIMAL: 20
    PKT. ERREICHT: ______
    Sei N die Länge des Inputs für einen Algorithmus A. Für manche Fälle ist es wichtig, den Zeitbedarf T(N) des Algorithmus A im worst-case-Fall berechnen zu können.
    1. Teilaufgabe - MAX.PKT: 6
      Übersetzen Sie den nachfolgenden Quellkode des Algorithmus in ein Struktogramm. 
       
//-------------------------------------------------------------
// Quadratic maximum contiguous subsequence sum algorithm. 
// seqStart and seqEnd represent the actual best sequence.
//
//-------------------------------------------------------------

.....  

template <class Comparable>
Comparable maxSubsequenceSum2( const vector<Comparable> & a,
                               int & seqStart, int & 
seqEnd )
{
    int n = a.size( );
    Comparable maxSum = 0;

    for( int i = 0; i < n; i++ )
    {
        Comparable thisSum = 0;
        for( int j = i; j < n; j++ )
        {
            thisSum += a[ j ];

            if( thisSum > maxSum )
            {
                maxSum = thisSum;
                seqStart = i;
                seqEnd = j;
            }
        }
    }

    return maxSum;
}

// Test program.

int main( void )
{ 
.....
  vector<int> test;         //Empty vector
  int ss = -1, se = -1;     // ss := SeqStart, se := SeqEnd 

.....
    2. Teilaufgabe - MAX.PKT: 10
      Konstruieren sie die Funktion T(N) des Zeitbedarfs des Algorithmus anhand des Zeitbedarfs der einzelnen Blöcke des Struktogramms (nur die Funktion maxSubsequenceSum2(), nicht das Testprogramm mit main()).
    3. Teilaufgabe - MAX.PKT: 2
      Übersetzen sie die Funktion T(N) in eine der vier Notationen O(f(N)), Omega(f(N)),Theta(f(N)),o(f(N)) und begründen Sie, wie sie diese Notation herleiten.
    4. Teilaufgabe - MAX.PKT: 2
      Wann benutzt man im Kontext der Berechnung des Zeitbedarfs eines Algorithmus in der Regel die log-Funktion? (Kurze Beschreibung des Problems und Begründung für den Einsatz der log-Funktion).

  3. Rekursion
    PKT. MAXIMAL: 17
    PKT. ERREICHT: ______
    Die Formulierung von Funktionen als rekursive Funktionen kann in bestimmten Fällen sehr vorteilhaft sein; birgt aber auch Gefahren.



    1. Teilaufgabe - MAX.PKT: 3
      Gegeben sei das folgende Problem P: Berechnen Sie mit einer Funktion seqsum(n) die Summe eines Anfangsabschnitts der natürlichen Zahlen von 1 bis n. Beispiel: seqsum(4) = 1 + 2 + 3 + 4 = 10. Definieren Sie die Funktion auf rekursive Weise.
    2. Teilaufgabe - MAX.PKT: 1
      Definieren Sie die Funktion seqsum(n)auf nicht-rekursive Weise.
    3. Teilaufgabe - MAX.PKT: 1
      Wie unterscheidet sich die rekursive und die nicht-rekursive Variante der Funktion seqsum bzgl. des Speicherbedarfs?
    4. Teilaufgabe - MAX.PKT: 10
      Für das Absuchen eines binären Baumes gibt es unterschiedliche Strategien. Eine heisst preorder. Beginnend bei der Wurzel des Baumes gibt eine preorder-Routine erst den Wert des aktuellen Knoten aus und dann die Werte der Nachfolger, von links nach rechts. Geben Sie eine rekursive Definition für die Routine printPreOrder() an. Benutzen Sie dabei --soweit wie möglich-- die Terminologie aus dem nachfolgenden Quellkode für Knoten in AA-Bäumen. 
      
.....  
template <class Comparable>
class AATree;

template <class Comparable>
class AANode
{
public:
    Comparable element;
    AANode    *left;
    AANode    *right;
    int        level;

    AANode( ) : left( NULL ), right( 
NULL ), level( 1 ) { }
    AANode( const Comparable & e, AANode *lt, AANode *rt, 
int lv = 1 )
      : element( e ), left( lt ), right( rt ), level( lv ) { }

public:

    void printPreOrder( ) const;
    friend class AATree<Comparable>;

};

template <class Comparable>
class AATree
{
  public:
    AATree( );
    AATree( const AATree & rhs );
    ~AATree( );
 
   // Recursive traversals, with printing
    void printPreOrder( ) const
      { if( root != NULL ) root->printPreOrder( ); }
.....
    typedef AANode<Comparable> Node;

  private:
    Node *root;
    Node *nullNode;

   .....
    5. Teilaufgabe - MAX.PKT: 2
      Angenommen, der binäre Baum aus dem nachfolgenden Diagramm Beispielsgraph Nr.1 sei gegeben; geben sie an, welche Werte Ihre Routine printPreOrder()in welcher Reihenfolge ausgeben würde.

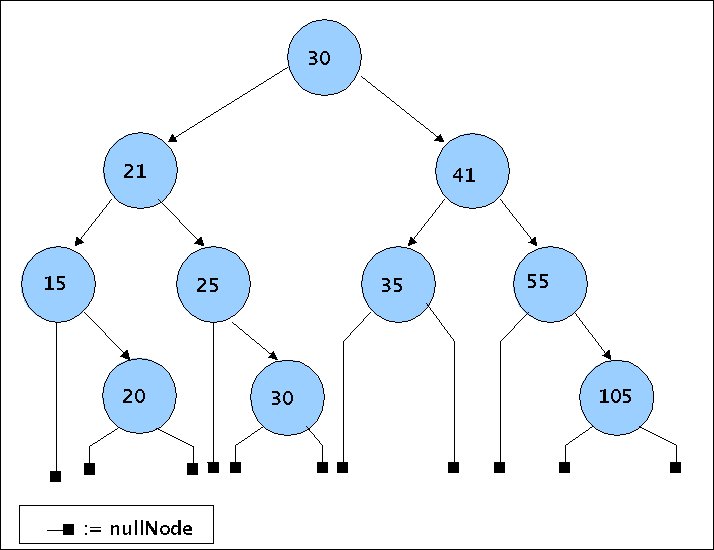
      graph1

      Beispielsgraph Nr.1


  4. Erzeugung von Pseudo-Zufallszahlen
    PKT. MAXIMAL: 9
    PKT. ERREICHT: ______
    In der realen Welt gibt es Ereignismengen, bei denen das Auftreten der einzelnen Ereignisse als zufällig bezeichnet wird. Es gibt keine Regel, anhand deren man das Auftreten eines bestimmten zufälligen Ereignisses fest voraussagen könnte. Für viele praktische Anwendungen ist die Verfügbarkeit von künstlich erzeugten zufälligen Ereignissen sehr nützlich. Meistens werden diese heute mit Pseudo-Zufallszahlen simuliert.
    1. Teilaufgabe - MAX.PKT: 2
      Geben Sie die Formel für den Linear Congruential Generator (LCG) an zusammen mit einer kurzer Kommentierung der Funktion der einzelnen Parameter.
    2. Teilaufgabe - MAX.PKT: 3
      Geben Sie C++-Kode für die einfache Implementierung eines LCGs an.
    3. Teilaufgabe - MAX.PKT: 2
      Ergänzen sie ihren Code für den LCG mit Optionen für Ausgabe im Bereich [1,upper] C INT sowie [0,1] C REAL
    4. Teilaufgabe - MAX.PKT: 2
      Geben sie einen Startwert I0 vor und berechnen sie die Folge der nächsten zwei Pseudo-Zufallszahlen ihres LCGs.

  5. Graphen
    PKT. MAXIMAL: 87
    PKT. ERREICHT: ______

    Für zahllose Probleme ist die Repräsentation des Problems mittels eines Graphen das Mittel der Wahl. Für die folgenden Teilaufgaben wird vorausgesetzt, dass die Basisversion eines Graphen wie in der Vorlesung notiert wird als GRAPH(g) gdw g = < V,E>.
    1. Teilaufgabe - MAX.PKT: 10
      Formulieren sie eine Definition für das Konzept topologische Sortierung.
    2. Teilaufgabe - MAX.PKT: 6
      Zeigen Sie, wie man mit dem Konzept der topologischen Sortierung beweisen kann, dass der nachfolge Graph im Beispielsgraph Nr.2 nicht zyklenfrei ist.

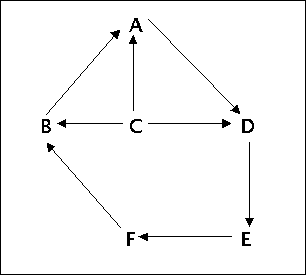
      topo1

      Beispielsgraph Nr.2

    3. Teilaufgabe - MAX.PKT: 15
      Konstruieren Sie einen Algorithmus, der das Konzept der topologischen Sortierung umsetzt.
    4. Teilaufgabe - MAX.PKT: 10
      Mit dem Konzept der reflexiven transitiven Hülle kann man die Menge aller Verbindungen in einem gerichteten Graphen definieren. Geben sie eine Definition für das Konzept der reflexiven transitiven Hülle.
    5. Teilaufgabe - MAX.PKT: 3
      Geben Sie am Beispiel des Beispielsgraphen Nr.2 alle Verbindungen an, die nach dem Konzept der reflexiven transitiven Hülle Verbindungen darstellen.
    6. Teilaufgabe - MAX.PKT: 18
      Konstruieren Sie einen Algorithmus, der das Konzept der reflexiven transitiven Hülle für den Bereich gerichteter Graphen umsetzt.
    7. Teilaufgabe - MAX.PKT: 8
      Rekonstruieren sie aus dem nachfolgenden Source-Kode das Struktogramm des Algorithmus unweighted() für die Suche nach dem kürzesten Weg in ungewichteten Graphen. 
      

struct Vertex;

struct Edge
{
                     // First vertex in edge is implicit
    Vertex  *dest;   // Second vertex in edge
    double   cost;   // Edge cost

    Edge( Vertex *d = 0, double c = 0.0 )
      : dest( d ), cost( c ) { }
 };


// Basic info for each vertex.
struct Vertex
{
    string        name;    // Vertex name
    vector<Edge>  adj;     // Adjacent vertices (and costs)
    double        dist;    // Cost
    Vertex       *prev;    // Previous vertex on shortest path
    int           scratch; // Extra variable used in algorithm

    Vertex( const string & nm ) : name( nm )
      { reset( ); }

    void reset( )
      { dist = INT_MAX; prev = NULL;  scratch = 0; }
};

// Initialize the vertex output info prior to running
// any shortest path algorithm.

void Graph::clearAll( )
{
    for( vmap::iterator itr = vertexMap.begin( ); itr != vertexMap.end( ); ++itr )
        (*itr).second->reset( );
}

// Single-source unweighted shortest-path algorithm.

void Graph::unweighted( const string & startName )
{
    vmap::iterator itr = vertexMap.find( startName );

    if( itr == vertexMap.end( ) ) {
      cerr << " startName is not a vertex in this graph" << endl;
     return;
      }

    clearAll( );
    Vertex *start = (*itr).second;
    list<Vertex *> q;
    q.push_back( start ); start->dist = 0;

    printName( (*itr).second ); //Control

    while( !q.empty( ) )
    {
        Vertex *v = q.front( ); 
        q.pop_front( );

        for( int i = 0; i < v->adj.size( ); i++ )
        {
            Edge e = v->adj[ i ];
            Vertex *w = e.dest;


            if( w->dist == INT_MAX )
            {
                printName( e.dest ); //Control
                w->dist = v->dist + 1;
                cout << "ACTUAL DISTANCE = " << w->dist << endl; //Control
                w->prev = v;
                q.push_back( w );
            }
        }
    }
}
    8. Teilaufgabe - MAX.PKT: 20
      Begründen Sie, warum dieser Algorithmus, ausgehend von einem Startknoten, alle möglichen kürzesten Wege findet.

  6. Binäre Suchbäume
    PKT. MAXIMAL: 48
    PKT. ERREICHT: ______
    Eine wichtige Teilklasse von gerichteten Graphen sind binäre Suchbäume.
    1. Teilaufgabe - MAX.PKT: 3
      Was sind binäre Suchbäume? Wieviel Zeit benötigt eine Suche in binären Suchbäumen?
    2. Teilaufgabe - MAX.PKT: 5
      Was unterscheidet balanzierte binäre Suchbäume von 'normalen' binären Suchbäumen? Welches Kriterium der Balanziertheit kennen Sie? Formulieren sie es. Wieviel Zeit benötigt eine Suche in balanzierten binären Suchbäumen?
    3. Teilaufgabe - MAX.PKT: 2
      Welche üblichen Operationen über binären Suchbäumen können die Balance ändern?
    4. Teilaufgabe - MAX.PKT: 18
      Beschreiben sie anhand der Operation insertion (skew(), split()) der AA-Bäume, auf welche Weise sich eine Störung der Balanziertheit regulieren lässt.
    5. Teilaufgabe - MAX.PKT: 20
      Versuchen Sie zu begründen, warum die Operationen skew() und split() das Kriterium der Balanziertheit zu gewährleisten vermögen.