
HMI/MMI/HCI
|
Methodology
As stated in the section about the biological limits of human persons while interacting with machines there is a central 'property' of human persons which is central to nearly every kind observable intentional behavior, and this is what psychologists call 'Memory'. Whether a human person is perceiving, thinking, planning, deciding, acting - no one of these psychological activities can be done without the inclusion of memory. Therefore it makes sense to have a closer look to this central property of the human cognitive architecture.
Following the concept of the section about the HMI Process (cf. the following table taken from this section)
| Data Type | T --> | EXP --> | D --> | EVAL -->(Back to previous stages) |
| P | (0)(5)(6) KNOW,T | |||
| S-R | (1)(5)(6) T' | (2)(5) EXP | (3)(5) ED | (4) EVAL |
| N |
We will start with some informal suggestions about memory from the domain of everyday knowledge. Then we will give some more detailed account of a S-R-based psychological theory T (model) and from this we will deduce some experimental settings EXP and measurements including some data D. This will lead to a first evaluation EVAL of the theoretical model. Because all this is a major task we can here only write some first sketchy version (besides the explanations in the lecture). These notes have then to be elaborated in the future.
Bootstrap Model T0?
The start with some theory T0 is always a bit arbitrary; whatever you will select, it will not be good enough. But it must be simple otherwise you can it not explain. The main work will go into the process of further refinement of the first theory T0 --> T1 --> ... --> Tk.
We take as a starting point the following texts: Anderson, J.R. (1989), Arbinger, R. (1984), Craik, F.I.M., & Levy, B.A.(1976), Heinecke, A.M. (2004), Hoffmann, J. (1982), Jüttner, C. (1979), Kintsch, W. (1982), Klix, F. (1980), Shiffrin, R.M. (1976), Sternberg, S. (1966), Strube, G. (1984), Wender K.F., & Colonius, H., & Schulze, H-H. (1980).
As you can see is the status of formalizing a S-R-based psychological theory very low; in fact only a few of these texts mentioned are coming close to a real formal theory, especially F.Klix. Our intention is clearly to establish such a theory. But before we will do this we want to introduce the idea behind such a theory.
Experimental Setup
We will start the theoretical bootstrap process with an experimental setting which has been designed by Saul Sternberg (1966) (see also discussion in (Arbinger, 1984:59ff))
| 1 | 3.7 s | Nothing |
| 2 | 1.2s | Digit out of {0, ..., 9} |
| ... | ... | There can be 1 to 6 digits in a sequence, each 1.2s and at a fixed locus |
| 3 | 2.0s | Nothing; at the end 'warning signal' announcing test stimulus |
| 4 | X.0s | Test Stimulus out of {0, ..., 9} ; User has to respond with 'y' (Stimulus is in sequence) or 'n' (Stimulus is not in sequence); |
| 5 | Goto (1) | After response feedback signal for 'correct answer' and 'not correct answer'; Goto 1 |
In his 1966-paper S.Sternberg reports the following data:
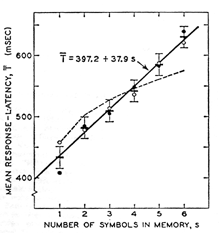 |
| Fig. 1. Relation between response latency and the number of symbols in memory, s, in experiment 1. Mean latencies, over eight subjects, of positive responses (filled circles) and negative responses (open circles). About 95 observations per point. For each s, overall mean (heavy bar) and estimates of o are indicated (6). Solid line was fitted by least squares to overall means. Upper bound for parallel process (broken curve).(from http://www.psych.upenn.edu/~saul/hss.html) |
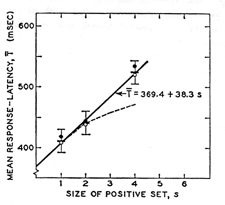 |
| Fig. 2. Relation between response latency and the size of the positive set, s, in experiment 2. Mean latencies, over six subjects, of positive responses (filled circles) and negative responses (open circles). About 200 (positive) or 500 (negative) observations per point. For each s, overall mean (heavy bar) and estimates of o are indicated (6). Solid line was fitted by least squares to overall means. Upper bound for parallel process (broken curve). (from http://www.psych.upenn.edu/~saul/hss.html) |
He interprets these data in the way that the elements of the finite sequence will be stored in some kind of a memory called short-term memory (STM). When the test stimulus occurs the user will internally search in the internally stored sequence of digits whether the test stimulus is an element of the finite sequence or not. What he is searching for is the function:
function_searched: number_of_stored_elements x test_element ---> response_time
Sternberg interprets his data as showing a linear dependency between number of items stored and response time. From this he induces the so called exhaustive scanning theory. The whole memory is searched item by item until the answer has been found. He is explicitly excluding a parallel interpretation because in that case the linear acceleration of the response time would not be interpretable.
A first sketchy theory T0
As is known from the cited references there is some widespread agreement that the memory can be partitioned in different kinds of 'modules' which are showing different functionalities. A very common partitioning is those in which one assumes a (i) sensory memory, (ii) a short-term (or primary) memory, and (iii) a long-term (or secondary) memory (cf. for an overview (Heinecke, A.M., 2004:ch. 3-5)). We will start here with a simplified model for to show than the further enhancement of the theory.
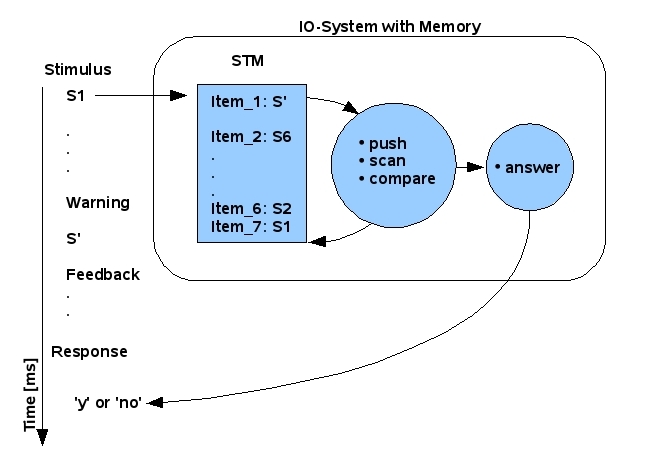 |
| Figure: Bootstrap Theory T0; Draft |
This theory assumes that the stimuli are directly transferred into the Short Term Memory (STM), which is organized as a FIFO (:= First In First Out). This means that the stimuli are stored by a kind of a 'push-action' which puts the last stimuli on top of the preceding stimulus. It is possible to 'scan' the content of the STM from Top to Bottom linearly. The actual scan-content can be compared to the top content. If the result of the comparison shows a certain kind of 'similarity' than does the top content 'match' the actual scan content; otherwise not. Depending on the result of the comparison can the system answer with a response action called 'yes' or 'no'. The response is given either when the system finds a 'match'-answer (and runs through until the 'end' of the STM) or if it finds a 'no-match-answer' until the end of the STM.
The system must be able to recognize when the end of the sequence is happening and the test stimulus occurs. Furthermore it must be able to identify the end of the sequence in the STM buffer.
This draft version of a first theory T0 has to be formalized as well as tested with real persons as well as with computer simulations. Additionally it can be compared with the conscious data of human persons as well as with neural findings. In an ideal case one could construct artificial neural networks representing the known neural structures which show as observable behavior exactly the T0 behavior and which are in correspondence with the conscious data.